聚焦单元 追求品质
——中央电教馆“教研共同体协同提升试点项目”活动纪实
2020-12-17张必华江苏省苏州高新区教育发展中心215163
张必华 (江苏省苏州高新区教育发展中心 215163)
胡永强 (江苏省苏州市阳山实验初级中学校 215151)
1 背景情况
如今,线上教学与教研方兴未艾.中央电教馆组织的“教研共同体协同提升试点项目”是基础教育领域落实国家精准扶贫政策的具体行动,张必华名师共同体(初中数学)教研团队有幸入选该项目.团队成员是从苏州高新区遴选出来的教育科研水平相对较高的初中数学骨干教师,与我们结对的是来自云南楚雄和孟勐、甘肃天祝、江西上饶、重庆石柱、四川雷波等中西部地区的一些学校.
2020年2月至7月,团队教研活动陆续开展.根据结对地区教师的需要,以人教版八年级下册数学教材为依托,团队成员分工协作做好章节单元教学分析和专题讲座,首先指定一名成员作为主备人,拿出初稿,然后团队全体成员共同参与研讨、打磨、修改,并交负责人审核,随后将研讨后的设计上传到中央电教馆全景学习平台.全国各地参与研讨的教师结合设计进行异步教研,提出自己的看法及困惑.随后,主备成员收集参加学习的教师的留言,并选取有代表性的内容融入重新修订的教学设计中.最后,主备成员在中央电教馆全景学习平台以直播形式向国内所有参加研讨的教师汇报自己的教材解读与建议,回答异步教研中教师们的一些问题,并进行线上互动.下面对活动开展半年多以来的过程及思考加以整理并与大家分享,不当之处,恳请批评指正.
2 如何做好单元教学分析与设计——以勾股定理一章为例
章建跃老师提出,单元教学设计要体现下列五条原则:数学的整体性、逻辑的连贯性、思想的一致性、方法的普适性、思维的系统性.事实上,就是要防止碎片化的数学教学!在这一思想的指导下,我们结合具体章节的实际情况,按照下列步骤实施单元教学分析与设计.
2.1 基础阅读——认真研读教材及课程标准
教材是教师教学和学生学习的重要文本素材,课程标准是确定教学目标、实施教学活动、检测教学效果的指导性文件.这两份材料是做好单元教学分析的必读素材.教材中本单元共包括三块内容,分别是勾股定理及其应用、勾股定理的逆定理及互逆命题等相关概念、测量旗杆高度及通过拼图法证明勾股定理的两个数学活动.《义务教育数学课程标准(2011年版)》对本单元提出的教学要求是:探索勾股定理及其逆定理,并能运用它们解决一些简单的实际问题.通过通读与细读教材,一方面可以明确本单元的一些具体知识点,另一方面可以理清教材的编排思路及特色.通过阅读课程标准,可以准确把握本单元的教学重难点.这些基础性的阅读为做好整体性、连贯性、系统性的单元分析打下了坚实的基础.
在阅读教材之后,对整个单元有了整体的认识,再思考连结本单元所有内容的线索.美国著名数学家及数学教育家M·克莱因说:数学史是数学教学的指南.数学教学分析与设计应当以史为鉴,于是便转入下一个环节,即广泛阅读相关数学史料,并有意识地收集整理.
2.2 扩展阅读——广泛涉猎本单元相关史料
通过查阅相关史料,发现勾股定理的历史十分悠久,世界上几乎所有古代文明的发祥地都有使用该定理的记载,相传古埃及人和古巴比伦人在公元前3000多年时就在生产、生活及天文历法中使用此定理.关于勾股定理的证明方法更是灿若星辰,至今已多达400余种.在我国,成书于西汉初年的《周髀算经》中记述了勾股定理的相关内容,这也是我国关于勾股定理的最早文字材料,因此这一定理又被称为商高定理.中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽.赵爽给《周髀算经》作了详细注释,运用“出入相补原理”证明了勾股定理.
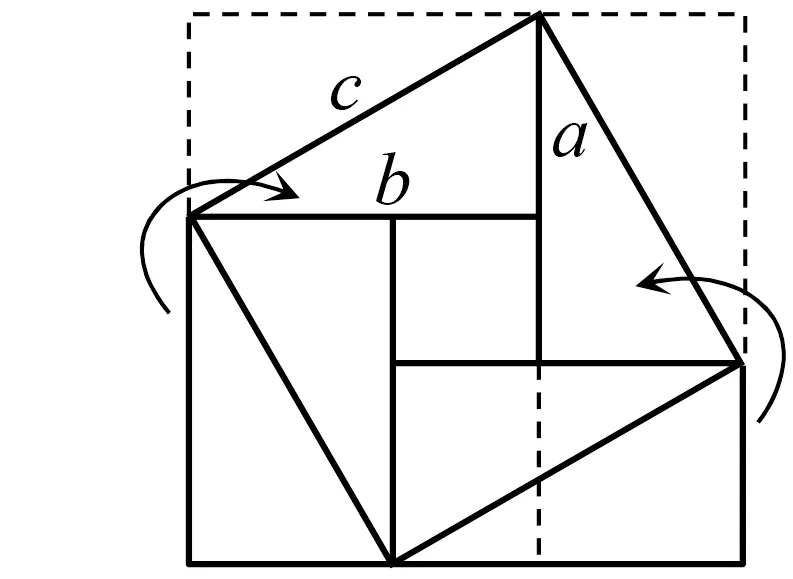
图1
有关勾股定理应用方面的史料更是数不胜数.在我国,成书于公元1世纪前后的《九章算术》中,第九章名叫“勾股”,这里一共记录了24道与勾股定理相关的问题.教材中也给出了一些历史上的经典名题.如第25页例2梯子靠墙问题,这道题与公元前2000年古巴比伦泥板BM85196号竿子靠墙问题同根同源;第29页习题第10题直接来自《九章算术》勾股章中的问题六“引葭赴岸”问题,与此类似的还有印度的风吹莲花问题;第36页数学活动1测量旗杆高度问题,来自《九章算术》勾股章中的问题七“立木系索”问题.上述问题均为勾股定理在实际问题中的应用.
对于勾股定理的逆定理在历史上留下浓墨重彩一笔的是“勾股数”的相关史料.现存美国哥伦比亚大学图书馆的“普林顿322号”泥版文书记录的是古巴比伦人关于勾股数组的研究结果,由此可以推断古巴比伦人业已掌握毕达哥拉斯三元数组的计算公式.古代埃及人在一段绳子上打上13个等距离的结,拉出一个三边为3, 4, 5的三角形,利用这个三角形中最大的角确定金字塔底座的直角是否准确.《史记》“夏本纪”记载说:夏禹治水,“左规矩,右准绳”.据推测,夏禹在治理洪水时是利用准绳(打了若干等距离结的绳)使用勾股定理的逆定理确定直角.这都是古人利用勾股定理逆定理判断直角三角形的具体事例.
上述史料为做好本单元整体分析和设计提供了很好的指导.我们可以在借鉴人类认识勾股定理相关内容的基础上进行适当的再加工,尽量让历史序、逻辑序和学生认知序统一起来,设计出更加符合学生认识规律的方案.
2.3 思考提炼——高观点下理解内容、做好设计
在阅读了整个单元的教材、课程标准及相关史料后,对单元整体内容的理解会变得更加全面而深刻,在此基础上用高观点理解和分析本单元内容,构建单元整体教学计划与具体教学设计方案.
勾股定理是平面几何学中三个最基本定理之一(另外两个定理分别是三角形内角和定理、相似三角形的判定定理),它在生产生活、数学、天文学、物理学等领域具有基础性的地位和作用.在数学内部,勾股定理是测望术的坚实的理论基础.初中阶段勾股定理常被作为解题时列方程的等量关系;高中阶段勾股定理是余弦定理的一个特例.勾股定理描述了直角三角形三条边之间满足的数量关系,是数形结合的典范.勾股定理的探究过程中蕴含了“观察-发现-猜想-证明”这一过程,可以较好地培养学生研究问题的能力,提高学生的数学素养.
2.4 立德树人——准确定位本单元的育人价值
《普通高中数学课程标准(2017年版)》指出:数学课程以学生发展为本,落实立德树人根本任务,培育科学精神和创新意识,提升数学学科核心素养.在做单元教学分析与设计时要深入挖掘数学学科的德育价值,在数学学科中落实德育工作,这已经成为数学教学分析与设计的一个重要维度.
勾股定理这一单元蕴含着丰富的德育价值,具体表现为:从《周髀算经》的相关记录可以知道我国古代劳动人民很早就使用勾股定理及其逆定理解决问题,《九章算术》更是为勾股定理专立一章,三国时期的赵爽第一个使用出入相补原理给出勾股定理的证明,之后的刘徽等人也给出了其他证法,清朝初期梅文鼎和晚期的华蘅芳更是给出了多种证法.这些历史素材可以很好地激发学生的爱国主义情怀,增强民族文化自信和文化自豪感.
2.5 集思广益——认真参加团队研讨
团队的智慧远远大于个人的智慧.在大家完成材料阅读、主线提炼之后,主备者拿出了初步分析方案并提交团队讨论.团队成员在充分阅读之后进行线上讨论,提出若干改进意见.主备者结合成员的意见对原方案进行修正,使之趋于完善,最后再提交领衔人审核.随后,主备者将修改完善后的方案提交网络学习平台,结对学校的教师借助该平台学习设计方案,并提出自己的一些观点与疑问.主备者再次结合教师们在网络上的留言,对方案进行适度修改,尽量将教师们的意见与疑问融入新的设计.最后,借助网络平台,以直播形式组织正式解读活动,主备者向所有参与研讨的教师作单元分析解读报告.在报告结束之后的互动环节,听课教师提出问题,主备者结合自己对本单元的理解进行回复.
3 如何做好专题讲座——以一次函数背景下的图形面积为例
3.1 研究确立专题讲座的设计模式
凡事预则立,不预则废.本教研共同体活动为初次举办的网络结对教研活动,没有现成的模式和经验可供遵循.本团队在组建之后不久的集中研讨会上,就围绕如何做好专题讲座展开讨论,集思广益,在听取团队成员的个人想法后,商定本团队专题讲座的基本形式及主要环节.经讨论,专题讲座大致包括以下四个环节:教学背景、教学分析、案例展示和教学思考.
在教学背景中应阐述所选专题的内涵、课程标准的相关要求、地位和作用及在中考中的概况等;在教学分析中应当包括设计者对课题的理解、教材分析、学情分析、教学目标及重点难点的分析等;在案例展示中要选取有代表性的例题,并在此基础上做好变式与拓展并及时总结提炼相关的解题策略、数学思想方法等;在教学思考中要对整个专题设计进行反思,提炼出有借鉴意义和价值的观点.
3.2 选取与章节内容高度相关的主题
所选的专题应当与章节内容高度相关且是本章教学的重点和难点的集中体现.因此,选题需要在深入思考的基础上进行分析、综合、择选,然后再展开设计.如在一次函数单元,选取函数图象下的三角形面积问题就是一个具有很好综合性与示范性的专题.这一专题中蕴含着丰富的数学知识及数学思想方法,学生在理解掌握计算与函数图象相关的三角形面积的方法后,对后续学习二次函数等内容有奠基性作用.
3.3 突出培养学生数学核心素养的主旨
专题讲座要以知识为载体、以问题为主线,集中体现数学思想方法,以培养学生数学核心素养为主旨.专题讲座是培养学生数学核心素养的良好方式,在准备专题讲座的过程中要用心发掘其中蕴含的数学核心素养,设计合宜的方案,将核心素养的培养落到实处,为学生后续更好地发展打好基础.
4 结语
单元整体分析是进行单元整体设计的前提,更是做好单元课时设计的基础.做好单元整体分析首先需要认真研读教材及课程标准,在此基础上再拓展阅读相关数学史料,进而思考与寻找知识发生发展的“源”与“流”.在完成基础性阅读之后需要用高观点来审视整个单元,把一些上位的数学思想、方法、精神提炼出来,同时要兼顾知识的历史序、逻辑序和学生认知心理序.需要结合本单元的具体特点寻找立德树人的载体,充分发挥好数学学科的德育功能与价值.在上述工作的基础上,做好单元整体分析设计,避免碎片化的教学.在完成设计初稿之后需要借助团队力量进行讨论修改,以使分析方案与设计趋于完善.
在单元整体分析与设计的基础之上,认真做好专题讲座,专题讲座应当围绕单元核心内容,提炼数学思想方法,培养数学核心素养.单元整体分析与设计和专题讲座相辅相成、相互补充.
