例说高中数学多项选择题的编制方法
2020-12-17江苏省镇江崇实女子中学212004
严 鹏 (江苏省镇江崇实女子中学 212004)
尤 裕 (江苏省梅村高级中学 214000)
《普通高中数学课程标准(2017年版)》在课程性质与基本理念一节中提到:把握数学本质,启发思考,改进教学.在课程目标中指出学生必须获得进一步学习及发展的“四基”,提高学生从数学角度发现和提出问题的能力、分析和解决问题的能力(“四能”).江苏省作为即将实施新高考的省份,数学试卷的命制将有新的调整,加入了多项选择题这一新题型.
多项选择题,又称多选题,新高考中的多选题是一种正确选项数多于1个少于4个的选择题题型.多选题典型的分值为5分,考生选出了一个或几个正确答案,但没有选出全部的,得2分;选错一个得0分;全部选对得5分.多选题是选择题的一种,解题时要认真审题,忌讳题目没有读清楚就开始埋头苦算,结果不但浪费了大量的时间,还会被选项中的干扰项干扰导致做错,结果事倍功半.因此,解题前一定要把题目读透,理解题目的条件后迅速联想涉及到的概念、公式、定理以及常见思想方法,发现题目中的隐含条件,理解题目的真正含义.另外,做选择题特别要注意解题方法.选择题和填空题、解答题不一样,正确选项一定在给出的选项中,所以做题时除了按照解答题的思路直接来求解以外,也可以使用一些其他的方法,比如说特殊值检验、选项代入法、排除法、数形结合法,等等.
多项选择题有效地考查了学生的“四能”.笔者认为,教师可以从以下几个方面去考虑多选题的编制过程,从而进一步改进教学,促进学生“四能”的提高.
1 将单选题中选择正确的选项,改成选错误的选项
这样的编制题目是比较容易操作的,但是对学生的能力训练不能达到预期目标.这类多选题本质上来说还是单选题.学生不能感受到该种题目作为多选题,与单选、填空之间的差异.
例1原题(2019全国Ⅰ卷理9) 记Sn为等差数列{an}的前n项和,已知S4=0,a5=5,则( ).
A.an=2n-5 B.an=3n-10
改编 记Sn为等差数列{an}的前n项和,已知S4=0,a5=5,则下列结论不成立的是( ).
A.an=2n-5 B.an=3n-10
这类问题可以用直接求解法求解.
2 将求范围的题目,改成求具体值的多选题
例2原题(2017全国Ⅰ卷理5) 已知函数f(x)在(-∞,+∞)上单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( ).
A.[-2,2] B.[-1,1]
C.[0,4] D.[1,3]
改编 已知函数f(x)在(-∞,+∞)上单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值可能是( ).
A.0 B.1 C.2 D.3
原题是给出函数性质,通过不等式的计算得到变量的范围.改编后变成满足不等式条件的变量值有哪些符合题意.这类问题可以使用直观分析法中的估值法来求解.
3 解题策略问题条件的选择
本类题目的设置一般是立足于开放性条件的变化,一个问题给出不同的条件会有多种解法.例如解三角形中的问题.
例3原题 苏教版必修5第14页例1(2);第 15页例4;第 18页例1;第 20页练习4.
改编 (2020崇实女中高一期中考试)镇江崇实女子中学的校园是非常美丽的.校园内,百年古树相交映,草色遥看近却无.走在学校的林荫大道上,享受“沾衣欲湿杏花雨,吹面不寒杨柳风”的感觉.可是,细心的同学会发现,林荫大道不是由直线构成的,而由两条路宽一样的道路拼接而成,有一个拐角.其中,第一段路面是和校门口所在直线垂直的,如图1所示.抽象出数学模型如图2所示,其中O,E为校门口左右两点,A,C为道路衔接处两点.

图1
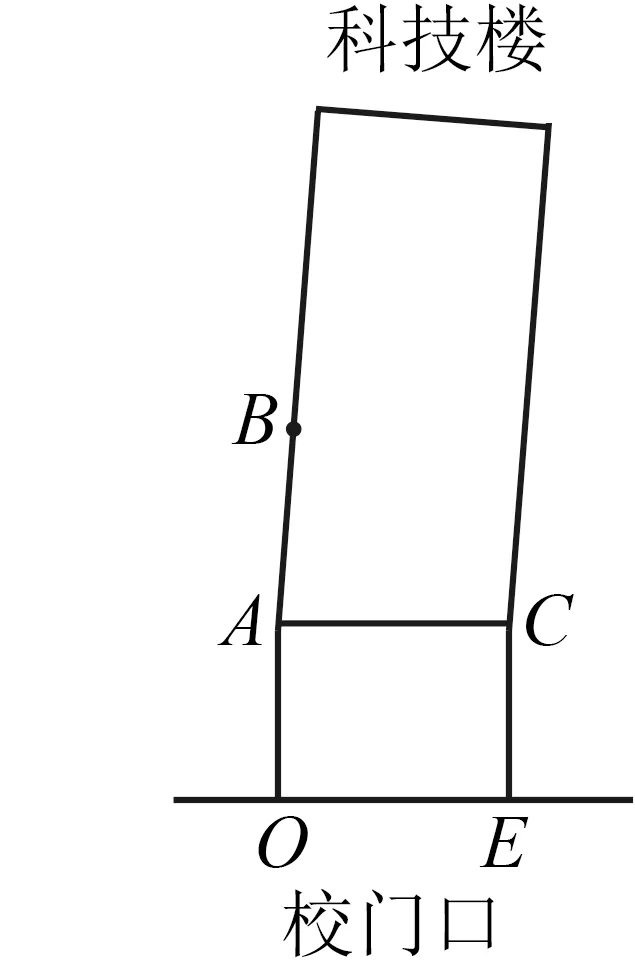
图2
怎样计算这个拐角OAB的角度或它的某个三角函数值呢?测量小组甲、乙、丙、丁四位同学给出了不同的测量方法,请问哪些同学给出的策略是能完成目标的?( ).
A.甲同学的策略:在第二段林荫大道路边任取一定点B,如图2所示.沿校门口点O出发,匀速走完路程OA,AB,BO,分别记录走完OA,AB,BO所用的时间t1,t2,t3.经过计算,就可以算出这个拐角OAB的余弦值.
B.乙同学的策略:用尺量出林荫大道的路宽和拐角处的两个点A,C间的距离.经过计算,就可以算出这个拐角OAB的余弦值.
C.丙同学的策略:用尺量出校门宽度,在校门E处测量出观察点O和点B的视角OEB.经过计算,就可以算出这个拐角OAB的余弦值.
D.丁同学的策略:在第二段林荫大道路边任取一定点B.自己眼睛到地面的距离为1.6 m,站在校门口O处,测量出看点A的俯视角和看点B的俯视角.在门口点E处,再测量出看点A的俯视角和看点B的俯视角.量出校门的宽度,经过计算,就可以算出这个拐角OAB的余弦值.
这类问题的处理,可以使用推理分析法中的逻辑分析法和特征分析法.
4 开放性问题的研究
一般传统数学题目答案唯一,而开放性数学题由于题目中的条件不够完备,需要自己设定分类讨论从而解出不止一解的答案.这类题目往往可以根据一个恒等式来隐藏部分条件进行编制.
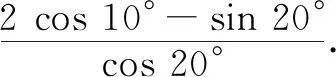
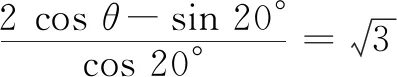
A.10° B.120° C.210° D.370°
这类问题可以使用间接法中的逆推验证法来处理.
5 题目本身就是多解
实际上,很多数学知识的产生都源于问题.有的题目本身就有多个解答结果,如求极值点问题.
例5函数3x5-5x3+1的极值点有( ).
A.-1 B.0 C.1 D.2
这类问题一般使用直接求解法解决.
6 概念的掌握和理解
学生对数学概念的掌握还需要通过运用,才能加深理解,真正成为自己的经验.学生要识别应该用什么概念,区别相似而又不相同的概念.因此,运用数学概念解答问题,可以巩固和加深对概念的理解,丰富对概念的本质特征的认识,培养学生对数学概念的选择、判断和联系的能力.
例6下列求导运算正确的是( ).
A.(ln 2)′=0
B.(cosx)′=sinx
C.(x2sinx)′=2xsinx+x2cosx
这类问题可以使用直观分析法或者间接法中的排除法来解决.
7 原题有多个结论
该类题型可以将结论修改成多项选择题的选项.
例7原题(2019全国Ⅰ卷理11) 关于函数有下述四个结论:
①f(x)是偶函数
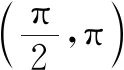
③f(x)在[-π,π]有4个零点
④f(x)的最大值为2
其中所有正确结论的编号是( ).
A.①②④ B.②④ C.①④ D.①③
改编 关于函数f(x)=sin|x|+|sinx|,下列结论正确的是( ).
A.f(x)是偶函数
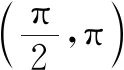
C.f(x)在[-π,π]有4个零点
D.f(x)的最大值为2
这类问题的解决,可以用直接法中的图象法或者推理分析法中的逻辑分析法.
解决多项选择题,不管用什么方法,能够得出正确答案的方法都可以尝试.做选择题要利用好正确答案在四个选项中的特点,全方面分析,帮助学生快速找出答案.在对编制题目理解的基础上,教师可以对多项选择的教学活动做出更好的预案.
