数学核心素养视角下的“双轨迹问题”赏析
2020-12-17凌海霞江苏省沙溪高级中学215421
凌海霞 (江苏省沙溪高级中学 215421)
近几年来,高考数学试卷及各地高考数学模拟试卷中常常出现“双轨迹问题”,除了考查数学相关知识与方法外,还重点考查了学生的数学运算、直观想象、逻辑推理等数学能力,符合课标倡导的课程教育目标.在数学高考复习中应该加强数学核心素养的培养,首要的任务是选择好相关的素材,通过引领、示范开展好数学课堂活动.
1 合理分解条件,培养学生的数学运算能力
解析几何是用代数方法处理几何问题.通过代数符号、数据进行数学运算,可以培养学生的数学运算能力.
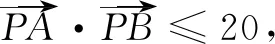
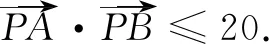
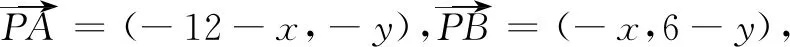
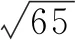
(说明:类似这样的一个动点满足同时在两个轨迹上的问题,我们称其为双轨迹问题.)
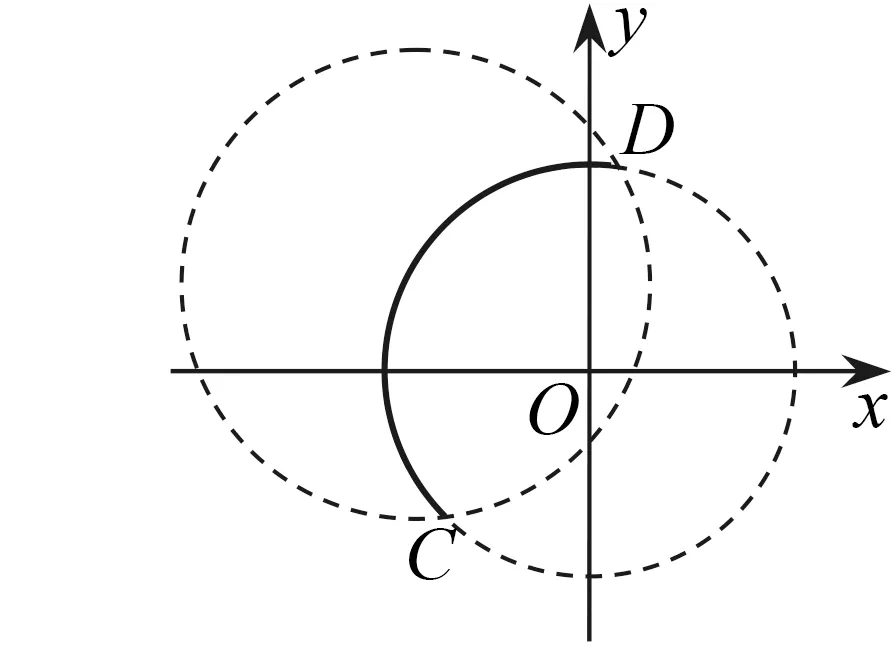
图1
说明 将条件①②分解开来,分别得到点P所在的两个轨迹,然后转化为两个轨迹的关系问题. 在解决该问题时,运用代数运算、分析和推断,培养学生的数学运算能力.
2 揭示数学本质,提升学生的数学抽象能力
从探究数学本质的角度来说,双轨迹问题大体可以分为两类:一类是可以转化为圆与圆的位置关系问题(如问题1),另一类是可以转化为直线与圆的位置关系问题(如下面的问题2).
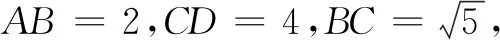
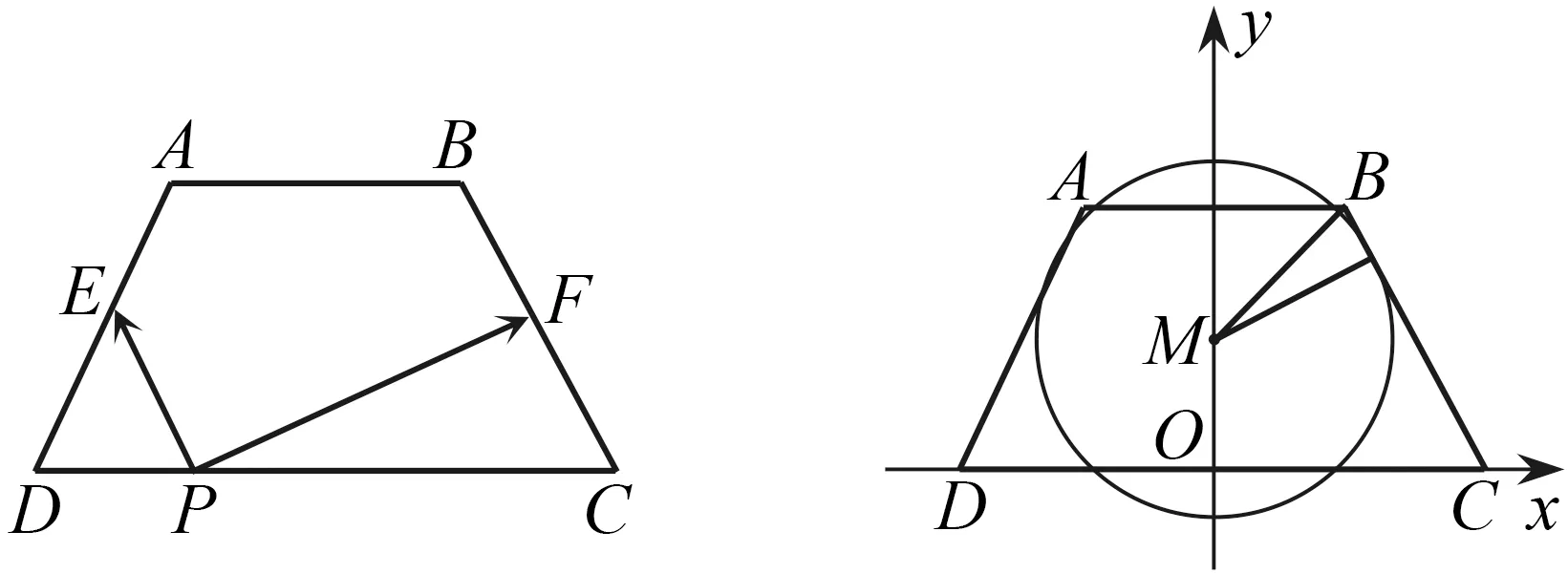
图2 图3

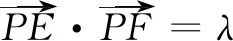
3 利用数形结合,增强学生运用直观想象的意识
直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形,理解和解决数学问题的素养[1].主要表现为:建立形与数之间的联系,利用几何图形描述问题,借助几何直观理解问题,运用空间想象认识事物.而是否有运用直观想象的意识是关键!
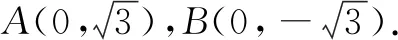
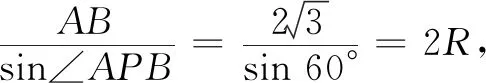

图4

说明通过数与形的相互转化,发展几何直观和空间想象能力,增强学生运用几何直观和空间想象思考问题的意识.
从问题1~3的分析可知,解决双轨迹问题分为两步:第一步,确定一个动点作为研究的对象,分解题目的条件,然后分别求该点的两个轨迹;第二步,针对所得的轨迹揭示问题的本质,然后采取相应的解决方法. 针对第一步,如果在问题中有多个动点,又是如何解决呢?
4 学会有逻辑地思考,培养逻辑推理能力
逻辑推理是得到数学结论、构建数学体系的重要方式,是数学严谨性的基本保证,是人们在数学活动中进行交流的基本思维品质[1].如何能够在比较复杂的情境中把握事物之间的关联,从而形成有条理、合乎逻辑的思维品质呢?
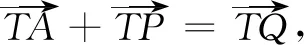

说明解答此问题要先对条件进行分析,确定研究的对象,通过逻辑推理得到结论.这是培养学生逻辑推理能力最有效的途径.
综上,解决双轨迹问题的难点有两个:(1)确定一个动点作为的研究对象,如果题目中出现多个动点,要首先确定起决定作用的点;(2)动点所在的两个轨迹中一般有一个是已知的,而另一个是隐含在条件中的,这需要学生要有轨迹意识,分析动点满足的几何性质或满足的等量关系,从而求得动点的轨迹方程.
