基于改进ILOS引导律的船舶循迹控制*
2020-12-17李超逸徐海祥余文曌
李超逸 徐海祥 余文曌
(武汉理工大学交通学院1) 武汉 430063) (高性能船舶技术教育部重点实验室2) 武汉 430063)
0 引 言
循迹控制是实现物体沿某一具体轨迹或跟踪某一目标运动的一种控制方法,要求物体以恒定速度沿预设轨迹运动.智能汽车、导弹发射、水面船、无人飞行器等都是此控制技术的具体运用[1].引导系统则是循迹过程中的重要环节,给船舶提供期望首向,让船舶尽快调整并进入预设航迹或实现预期的控制目标.在给定期望速度和期望航迹的条件下,line-of sight(LOS)引导律为欠驱船舶提供期望航向角,将控制系统的控制力代入船舶运动数学模型进行解析,得到当前时刻的船舶航速与首向信息,形成闭环系统,见图1.在此过程中,船舶将受到缓变环境力的作用,而欠驱船舶无法满足横向下发控制力的功能,因此在运用LOS引导律的过程中会产生明显的横向偏差.针对该问题,学者们已经进行了相关研究,研究主要从控制器改进与LOS引导律算法改进两方面着手.
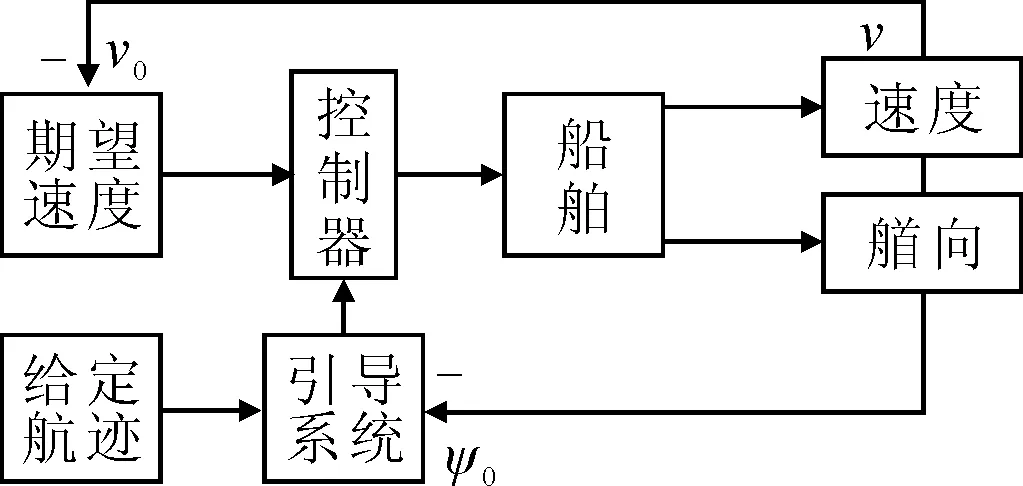
图1 引导系统工作原理图
在控制器改进方面,Fossen等[2]设计带有积分项的反步积分控制器,在运用LOS引导律循迹过程中能有效缩小横向偏差.徐海祥等[3]考虑到反步积分控制器的输出控制力包含脉冲现象,不利于控制力的分配,将动态执行机构加入反步积分控制器的设计中,形成一种控制分配算法,得到更加平稳的控制力.陈俊等[4]同时考虑了横向偏差、速度和艏向控制量,运用反步法设计了一种新的控制律,并通过仿真验证了其有效性.这些针对控制器的改进起到了降低横向偏差、平缓控制力的作用,但降低的幅度较小.
在引导律算法改进方面,Børhaug等[5]考虑了缓变流的影响,在传统LOS引导律算法的基础上,加入积分项,并验证了该方法的合理性.Lekkas[6]在Børhaug等基础上进行进一步改进,为使参数更加易于调整,将船舶航速设计进入ILOS引导律算法中,经仿真证明了其有效性,但由于航速作为循迹的控制量,使得该ILOS引导律算法受限于船舶航速.瞿洋等[7]在以上学者的基础上,在ILOS引导律的设计中加入了时变项,有效改善了参数灵活性与航速制约性.以上基于LOS引导律加入积分项的改进,虽然能大幅度降低横向偏差,但仍存在超调现象及降低系统的整体响应速度等不足之处.
本文针对目前方法的不足,提出一种改进ILOS引导律,在大幅度降低横向偏差和超调量的同时,提升了系统整体的响应速度,并分析了Lyapunov稳定性,通过仿真验证了该方法的可行性.
1 船舶运动数学模型
为便于描述船舶的循迹运动过程,本文建立图2的大地坐标系O0-x0y0z0和随船坐标系O-xyz,其中随船坐标系原点O即为船舶重心位置G,O0x0轴指向正东,O0y0轴指向正北.
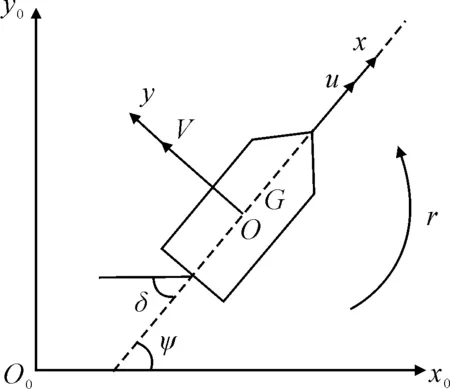
图2 船舶大地坐标系和随船坐标系
图2中的参数定义见表1.

表1 船舶运动参数及符号定义
本文采用欠驱船舶简化三自由度数学模型:

(1)
(2)
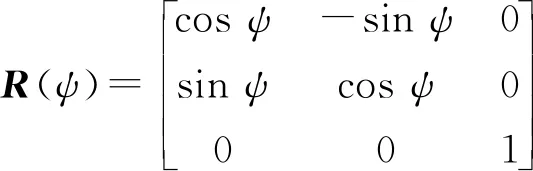
2 LOS引导律
为具体描述船舶在LOS引导律作用下靠近航迹的过程,建立图3的LOS原理图.其中船体坐标系为X0Y0,原点位置为(x0,y0).再以(xp,yp)为原点建立右手坐标系XppYpp.
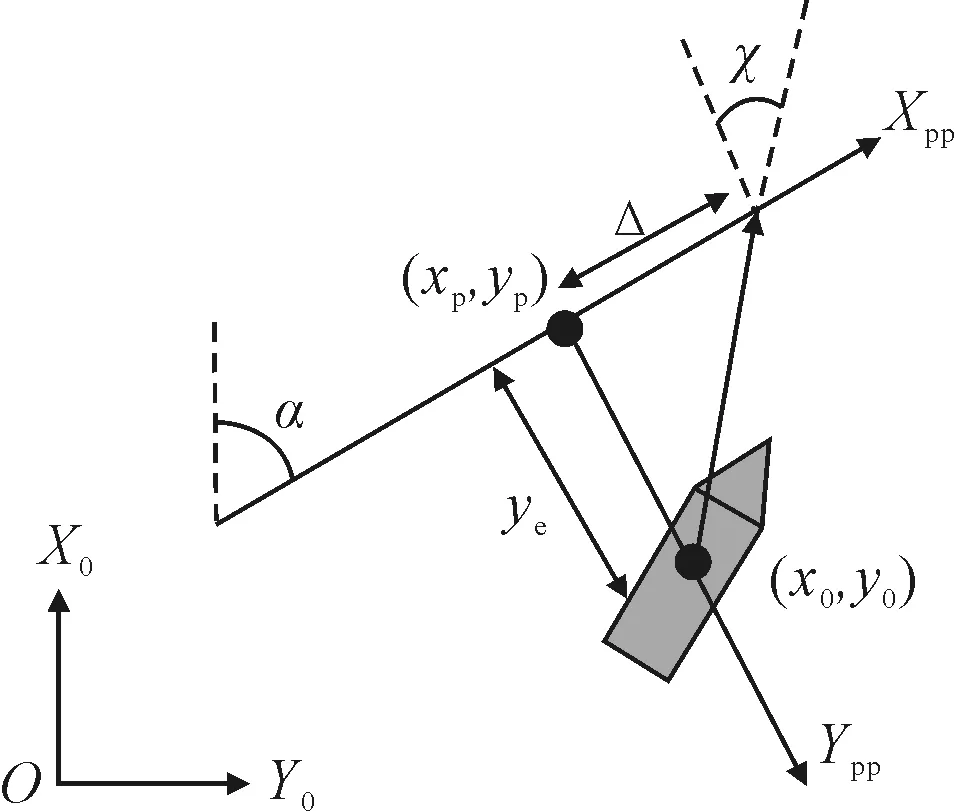
图3 直线路径LOS引导律原理图
在坐标系XppYpp下,船体与期望航迹的位置偏差为
(3)
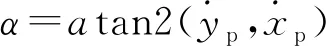
由式(3)可得横向偏差ye:
ye=-(x0-xp)sinα+(y0-yp)cosα
(4)
则船舶运动学方程为[8]
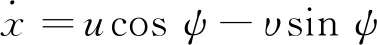
(5)
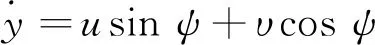
(6)
将式(4)求导并代入式(3)、式(5)、式(6)得:
(7)
式中:U为期望航速;χ为期望航向角.
(8)
将式(8)代入式(7)得:
(9)
3 ILOS引导律
3.1 传统ILOS引导律
传统ILOS引导律在期望航向角中加入积分项的同时,还增加了比例参数和积分参数.
χ=α-arctan(kpye+kiyint)
(10)
(11)
式中:kp,ki为系统参数;yint为积分项.
3.2 改进ILOS引导律
针对目前方法不能在消除横向偏差的同时保证系统快速响应的问题,提出了以下改进的ILOS引导律.
χ=α-arctan(kpye+yint)
(12)
(13)
式中:kp为比例参数(kp≥1),用于加快系统响应速度;ki为时变虚拟控制参数,
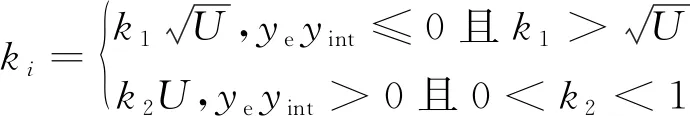
(14)
其中:k2为时变参数,
(15)
式中:kmax,kmin为时变参数k2的最大与最小值,参数ρ越小,kmax越大,积分效果越强.
3.3 Lyapunov稳定性分析
为便于下述稳定性证明,引入两个假设及两个引理作为证明条件.
假设1:kp≥1

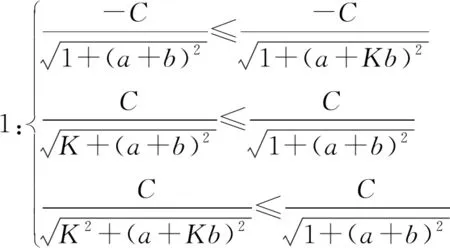
(K≥1,a≥0,b≥0,C>0)
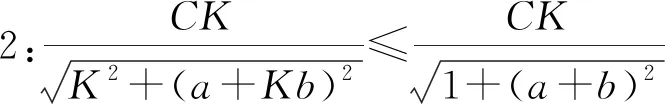
(0
将式(12)代入式(7),由引理1可得:
(16)
当Δ≥1时,由引理1可得:
(17)
取如下Lyapunov函数:
(18)
对式(18)两边求导并将式(16)和式(17) 代入式(18)可得:
(19)
对式(19)进行分析.
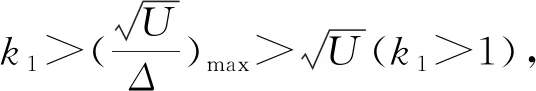

即证式(19)<0,系统全局渐进稳定.
当0<Δ<1时,由引理2可得:
(20)
取如下Lyapunov函数.
(21)
对式(21)两边求导并将式(16)和式(20) 代入可得:
(22)
对式(22)进行分析.
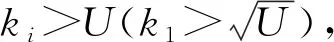
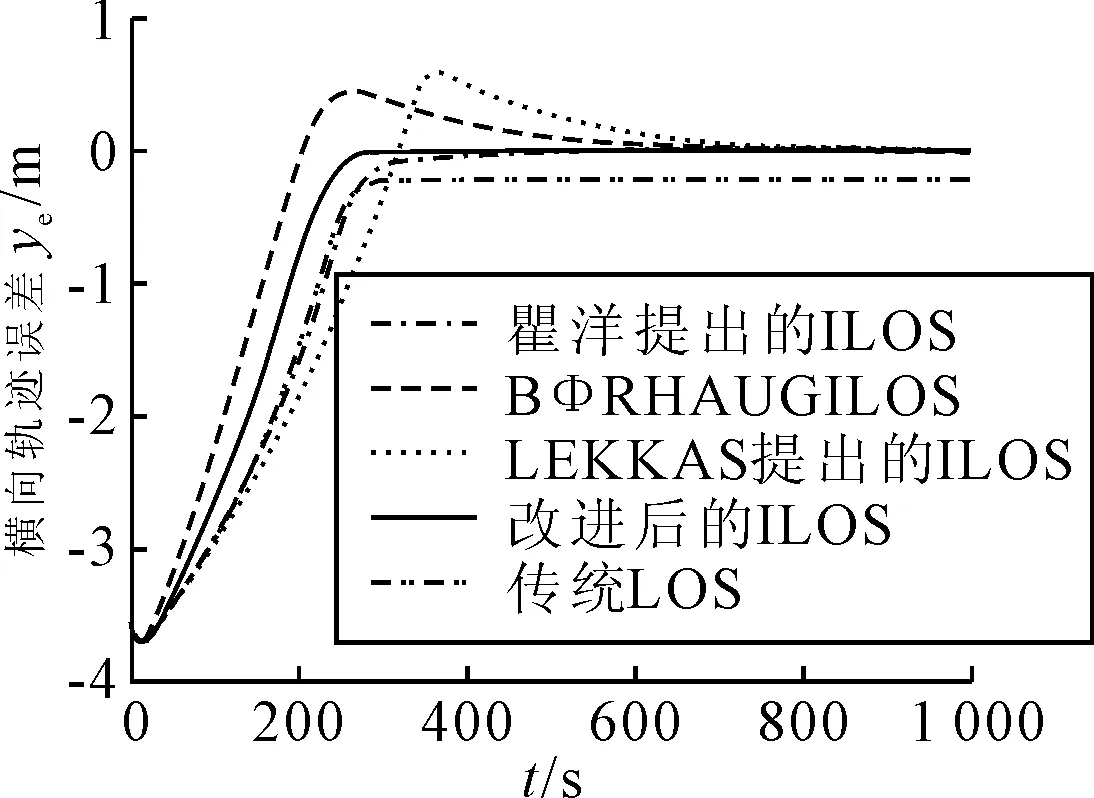
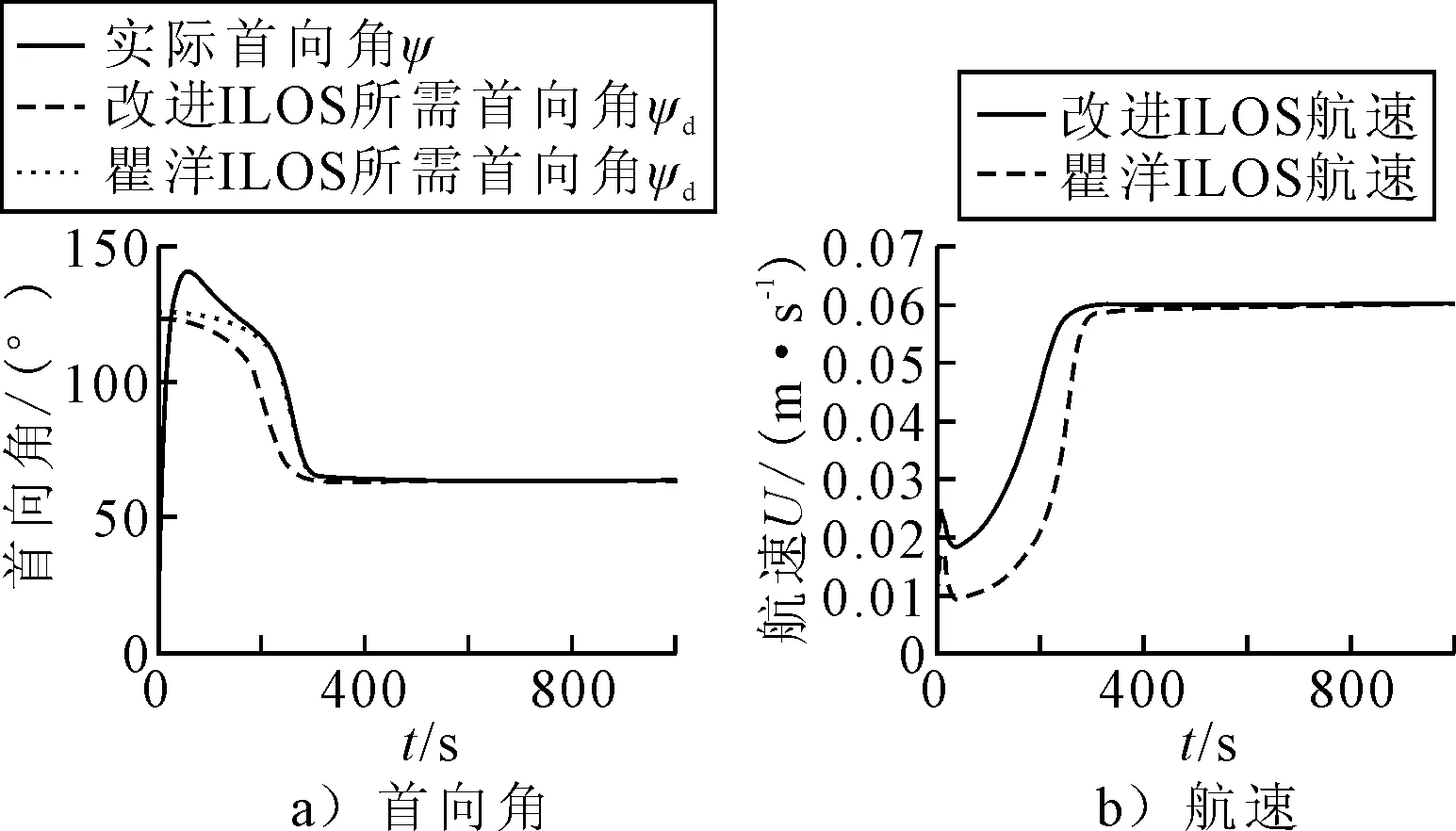
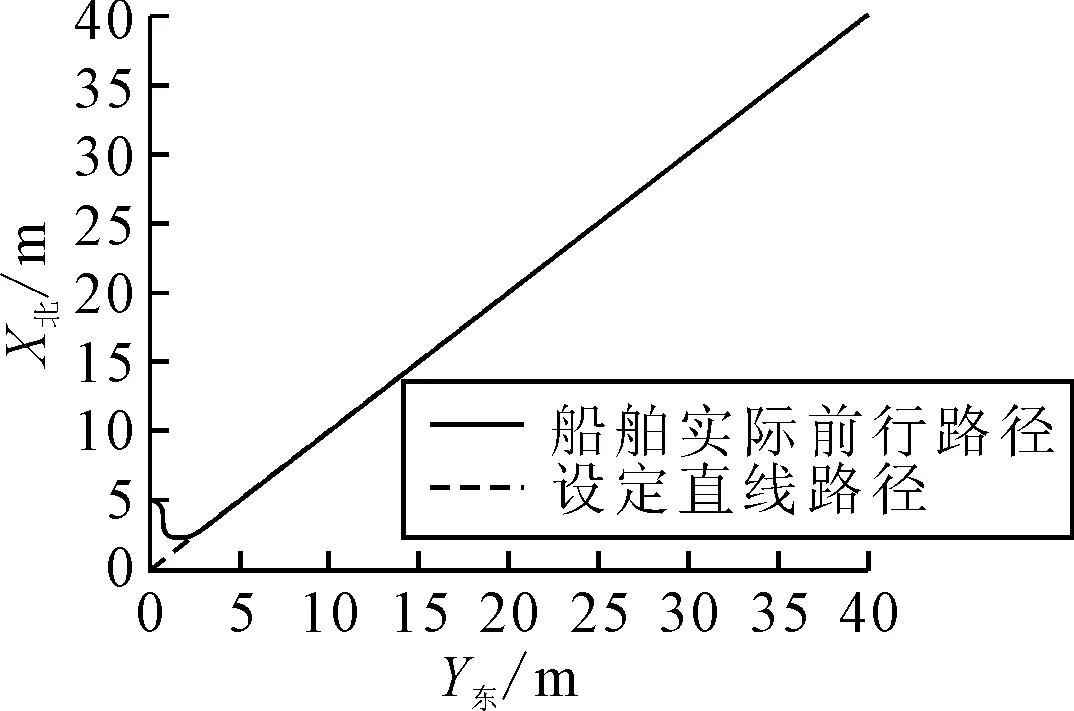
2) 当yeyint>0时,ki-U<0,即ki 即证式(22)<0,系统全局渐进稳定. 综上可知,改进ILOS引导律满足Lyapunov全局渐进稳定性. 本文采用文献[7]中的控制方法,针对速度偏差量采用PI控制,针对艏向偏差量采用艏向滑模控制,文献[6]已证明了该控制器的稳定性. 定义速度偏差eu. eu=u-ud (23) 式中:u为船舶实际运动速度;ud为船舶理想运动速度. PI控制律为 τu=-Kpeu-Kiε (24) (25) 式中:Kp为比例参数,其值越大速度收敛越快,相应控制力也随之变大;Ki为积分参数,其值越大积分效果越强. 将一阶船舶操纵运动方程(野本方程)引入艏向控制之中,得到如下控制律. (26) (27) 式中:T为船舶追随性指数;K为船舶回转性指数;δ为舵角;b为计算得到的环境力. 定义首向偏差方程. (28) 定义如下滑模面. (29) 式中:λ为滑模参数,λ>0. 定义新滑模面, (30) 控制律最终为 rr=r-s (31) (32) 式中:Kd为控制参数(Kd>0),γ≥bmax. 为验证改进ILOS有效性,对其进行直线循迹仿真,并与传统LOS引导律及文献[5-7]中提出的ILOS引导律方法进行仿真对比.仿真中使用武汉理工大学的平台供应模型船,参数见表2. 表2 仿真参数 图4为5种不同引导律算法的横向偏差仿真对比结果.由图4可知,传统LOS引导律曲线光滑,无明显的超调现象,收敛速度较快,于300周期收敛,但存在0.2 m的横向偏差.文献[5-6]提出的ILOS大幅度降低了横向偏差,其横向偏差值最终收敛至0,但分别存在0.45及0.6 m的超调量,且大大降低了系统的收敛速率,分别于600和800 s周期收敛.文献[7]提出的ILOS同样将横向偏差减小至0,并且曲线更加平稳,消除了超调现象,但系统响应速度同样较慢,于400 s周期收敛.本文提出的改进ILOS在未超调的情况下将横向偏差降至0附近,同时加快了系统的响应速度,于300 s周期收敛,综合性能最优. 图4 横向偏差对比图 文献[7]的方法相较于传统LOS和文献[5-6]中的ILOS有一定优势,为进一步验证改进ILOS的综合性能,本文进一步与文献[7]所提方法进行艏向角和航速的仿真对比,见图5.由图5a)可知,两种ILOS引导律收敛速度大致相同,但改进ILOS曲线更加平滑,响应速度更快.由图5b)可知,文献[7]提出的ILOS引导律航速于600 s周期收敛至期望航速,改进ILOS引导律于340 s周期收敛至0.06 m/s,且无超调现象,在航速方面同样占据优势. 图5 首向角和航速对比图 为进一步验证改进ILOS的循迹效果,图6为期望航迹与实际航迹的仿真对比.由图6可知,船舶于起始点(0,5)开始运动,于(2.5,2.5)位置处运动至期望路径,之后能够沿着期望路径保持航行稳定性,验证了该方法的有效性. 图6 航迹图 针对传统LOS循迹产生较大横向偏差及ILOS循迹中系统响应速度较慢的问题,提出了一种基于固定前向距离及时变虚拟控制参数的改进ILOS引导律,经过Lyapunov分析,证明了该算法的稳定性.结合纵向PI控制器和艏向滑模控制器,通过与其他4种不同引导律进行仿真对比,验证了该算法能够在解决横向偏差的同时,消除超调量并提升系统整体响应速度.4 控制器设计
4.1 纵向PI控制器
4.2 艏向滑模控制器
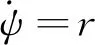
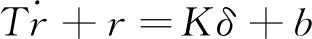
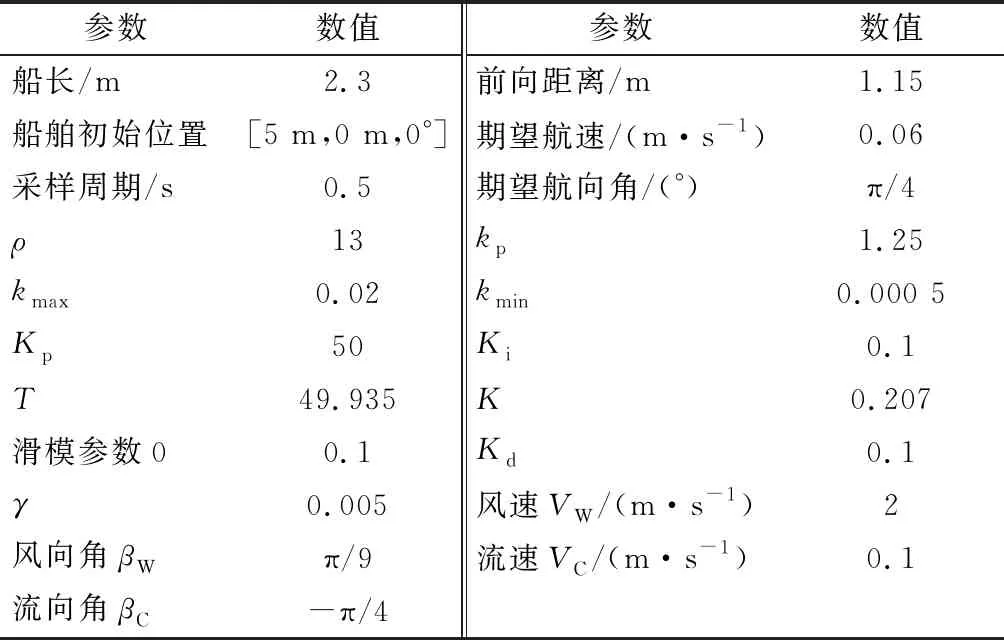
5 仿真结果与分析
6 结 束 语
