基于改进卡尔曼滤波的配电网动态数据平差方法
2020-12-16刘科研盛万兴胡丽娟
刘科研, 盛万兴, 胡丽娟
(中国电力科学研究院, 北京 100192)
近年来,随着全国联网和能源资源大范围优化配置格局的初步形成、电力市场化改革进程的稳步推进,配电网结构日益庞大,电网中产生了海量的数据[1]。由于受测量设备与外界条件等因素的影响,量测结果必然会带有误差。为了有效处理存在误差的量测数据,应在实际应用前对其进行数据平差分析计算。其目的是选用合适的估计方法,求出未知量的最佳估计值。传统平差方法如加权最小二乘法、快速分解状态估计法、量测量变换状态估计法等[2]仅适用于静态系统,而实际上配电网为一动态系统,其参量会根据电源出力、负荷变动而波动。要对配电网量测数据进行数据平差需要用到动态估计方法。
目前广泛应用的动态估计以扩展卡尔曼滤波(extended Kalman filter,EKF)为主,但在线性化的时候需要用到Jacobian矩阵,在维数较高时会存在正交项,在实现时容易发生错误[3]。因此,Julier等[4]提出无迹卡尔曼滤波(unscented Kalman filter,UKF)算法,随后又提出了含有比例因子的UKF方法[5]。文献[6]利用矩阵Cholesky分解方法提出了平方根形式的UKF。但由于系统噪声特性较难获得,文献[7]基于改进的次优Sage-Husa法提出了一种自适应UKF方法,加入噪声估计器来补偿系统噪声的影响。通常情况下的噪声为高斯白噪声,大部分状态估计模型也都是以此为前提,然而实际的系统模型并不精确,往往存在量测粗差,这些不良数据会引发“残差淹没”或“残差污染”现象。为解决此问题,文献[8]提出了电力系统抗差估计计算方法。抗差估计的目标是指在粗差不可避免的情况下,选择适当的估计方法,得到最佳的估计值。具体方法有通过增强因子对系统量测噪声进行修正的改进UKF方法[9]、以合格率最大为目标的估计方法[10]、含指数型目标函数的估计方法[11]等。
许多方法中不良数据的检测阈值设定为固定值,但在实际应用中,固定阈值会导致不良数据的漏检和正常数据的误检。为此,提出一种鲁棒无迹卡尔曼滤波方法(robust unscented Kalman filter,RUKF)。结合运行模式概念,根据量测值的变化趋势改变阈值,对系统量测数据进行检测,修正不良数据,最后在IEEE 33-bus测试系统与某107节点系统上进行仿真实验,证实了本文算法相比于传统UKF具有更好的平差效果。
1 配电网动态模型
配电网的状态方程与量测方程为

(1)
式(1)中:xk为k时刻的n维状态向量;yk为k时刻的m维量测向量;f(x)为状态转移函数;h(x)为系统量测函数;qk为系统误差;rk为量测误差。两者均为服从高斯分布的白噪声。
系统的动态模型采用二次指数平滑法,如式(2)所示,相比于一次指数平滑法,此方法考虑了数据的趋势,具有更好的平滑效果[7]。

(2)
式(2)中:sk为k时刻平滑后的值;tk为k时刻平滑后的趋势;αH与βH均为参数,也可称为记忆衰减因子,表示越临近k时刻的数据权重越大,取值范围为[0,1];s和t初始值的选取对算法整体影响不大,通常取值为s0=x0,t0=x1-x0。
2 RUKF数据平差方法
2.1 基于运行模式的不良数据检测
在现代配电网系统中,受用户行为、气候因素等原因的影响,负荷的变化是有一定规律的,且具有明显的日相关性和季节相关性。因此可分为不同的运行模式。
基于3σ准则[12],在不良数据检测与辨识中,一般认为量测误差大于±3σ的量测量为不良数据。因此在状态估计中关于不良数据检测的阈值设定为±3σ。但在实际应用中,尤其是在相关不良数据的影响下,往往会出现“残差淹没”或“残差污染”现象,从而导致滤波效果下降甚至发散[13]。
因此,在状态估计中使用固定阈值是十分不妥的。结合运行模式概念,提出一种用于前置滤波的随量测量变化趋势调整阈值的方法,具体描述如下。
首先设定一个初始阈值δ0进行前置滤波,然后运行状态估计程序,将k时刻的估计值Xk与量测值求差得到ΔXk,其与估计值之比为

(3)
随后对阈值δk进行更新:

(4)
式(14)中:m为取值范围为[4,10]的常数[13]。
根据式(4)计算的阈值δk,检测不良数据。ΔCk为量测值yk与yk-1差的绝对值,即
ΔCk=|yk-yk-1|
(5)
若ΔCk>δkyk-1,则认为量测量yk为不良数据,则舍弃该测量值,然后使用估计值代替量测值。
2.2 UKF动态状态估计方法
针对卡尔曼滤波非线性效果差的问题,Julier提出了无迹卡尔曼滤波[4],该滤波方法的关键在于无迹变换(unscented transform,UT)。
2.2.1 UT变换
2.2.1.1 选取采样方式
UT变换通过确定的采样方式决定Sigma点的个数、位置和权值。由于配电网状态量维度较高,在计算时会产生局部效应和高阶项误差[14-16],选用比例修正的对称采样方法。
(6)
λ=α2(n+κ)-n
(7)

均值与方差的权值为

(8)
2.2.1.2 生成采样点


(9)

(10)

2.2.1.3 非线性变换
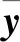
(11)

(12)
2.2.2 UKF预测
根据k-1时刻的状态量xk-1和协方差Px,构造Sigma点集{χi,k-1}[18]。
χi,k|k-1=f(χi,k-1)+qk-1
(13)

(14)

(15)
根据量测方程计算得到yi,k。
yi,k=h(χi,k-1)+rk-1
(1)The products are nice,but theprice is alittlebit high.
(16)
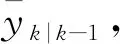

(17)

(18)

(19)
2.2.3 UKF更新
计算k时刻卡尔曼增益Kk、状态量估计值xk和协方差Px。

(20)

(21)

(22)
2.3 算法步骤
RUKF数据平差流程如图1所示,具体步骤可描述如下[19]。
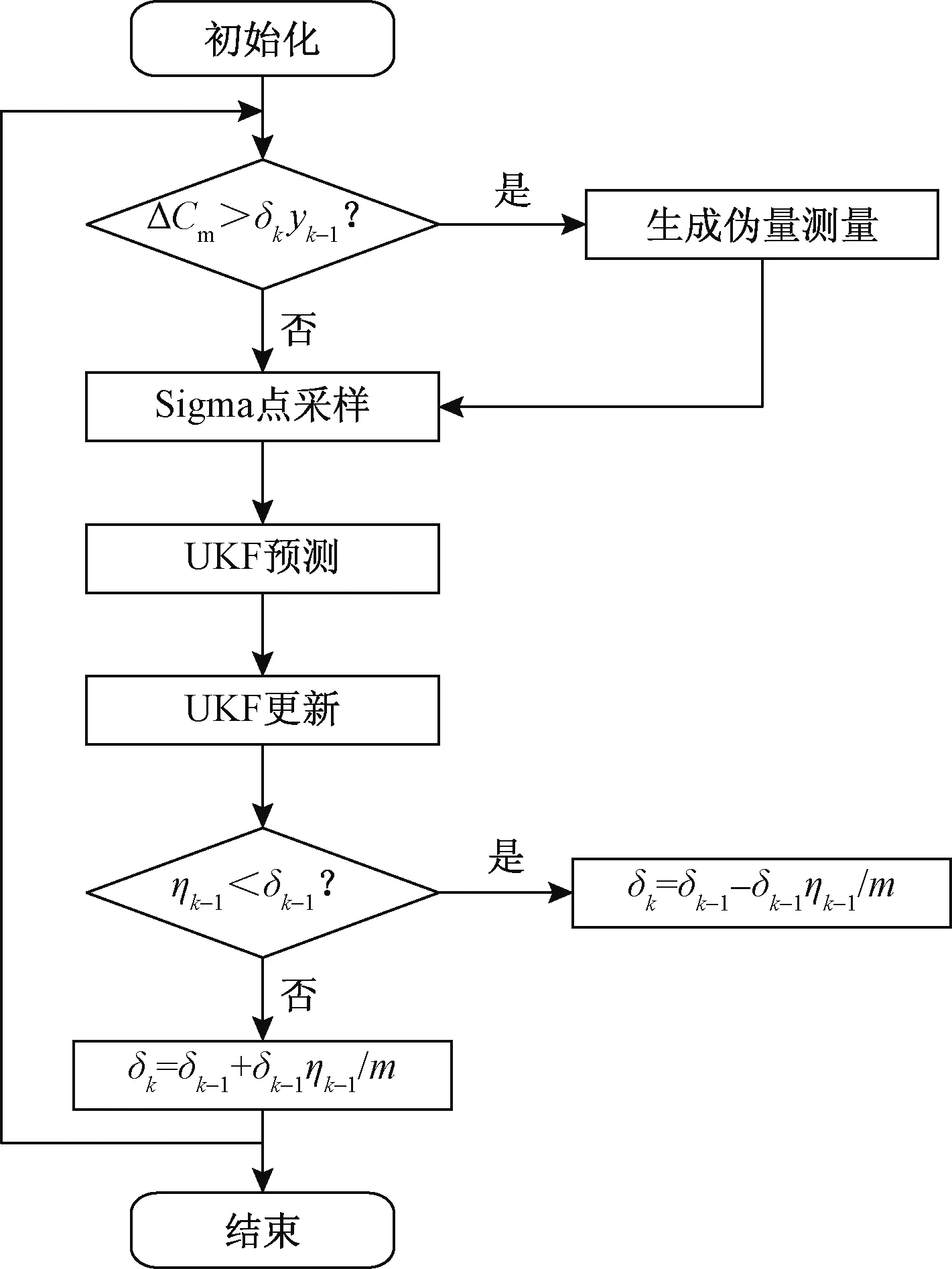
图1 RUKF数据平差流程Fig.1 Flow chart of RUKF data adjustment

步骤2按照式(13)~式(19)开始UKF预测步骤,得到k时刻y的预测值,协方差矩阵Sk和互协方差矩阵Ck。随后按照式(20)~式(22)计算k时刻卡尔曼增益Kk、状态量估计值xk和协方差Px。
步骤3根据所提基于运行模式的不良数据检测方法,判断数据变化趋势,按照式(3)、式(4)计算更新阈值,作为下一轮的不良数据判别标准。
步骤4从第二轮开始,在UKF前进行前置滤波,检测不良数据,并生成伪量测值代替不良数据。
3 算例分析
为了衡量平差效果,采用绝对误差(absolute error,AE)的平均值和最大值作为性能指标[1]。计算公式为
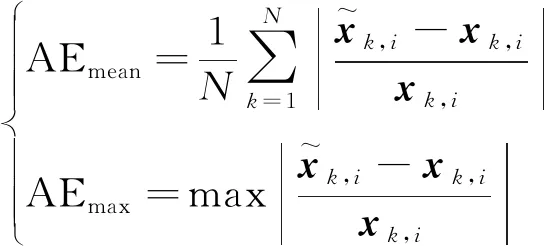
(23)
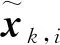
下面利用IEEE 33-bus与某107节点系统进行仿真实验。设定系统每10 min采样一次,一天共144个采样点。电压幅值量测误差的标准差为0.002,均值为0;电压相角量测误差的标准差为0.005,均值为0。Sigma点采样方式选用比例修正的对称采样方法,其中α=1,β=2,κ=0。系统状态方程使用二次指数平滑法,两参数αH取0.95,βH取0.05。为验证在存在不良数据的情况下RUKF的鲁棒性与稳定性,随机选取10个时间点的测量值,增大或减小随机数值,作为不良数据[20-21]。
3.1 IEEE 33-bus测试系统
首先在IEEE 33-bus测试系统上进行仿真实验,接线图如图2所示。在每个节点实际负荷的基础上叠加5%的波动,以仿真结果作为真值,在真值的基础上加入均值为0的高斯白噪声作为量测值。仿真结果如图3所示,绝对误差对比如表1所示。
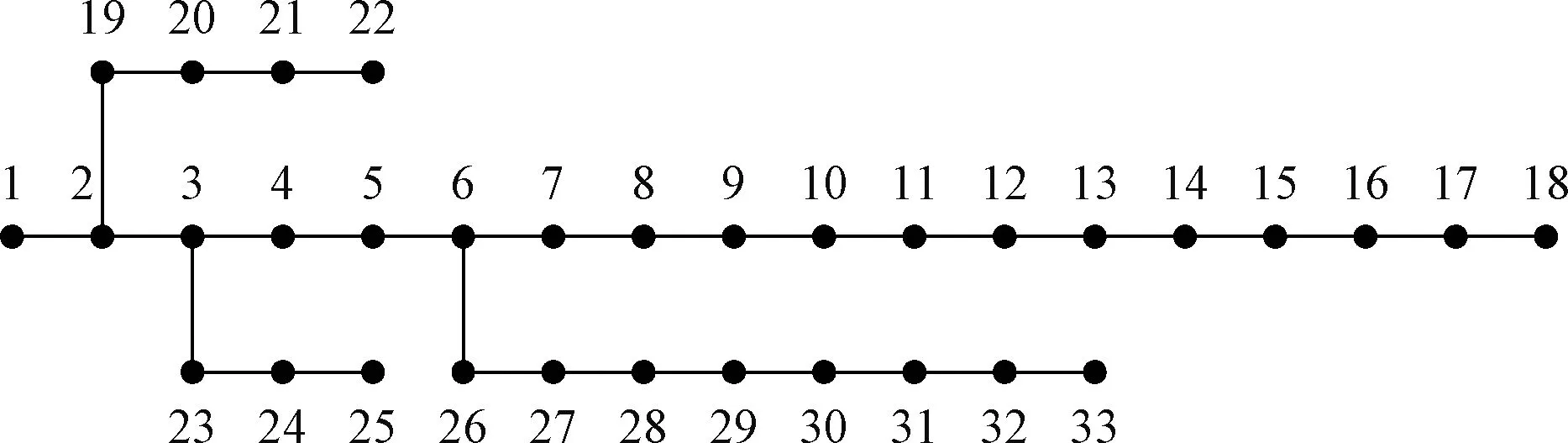
图2 IEEE 33-bus系统接线图Fig.2 IEEE 33-bus system wiring diagram
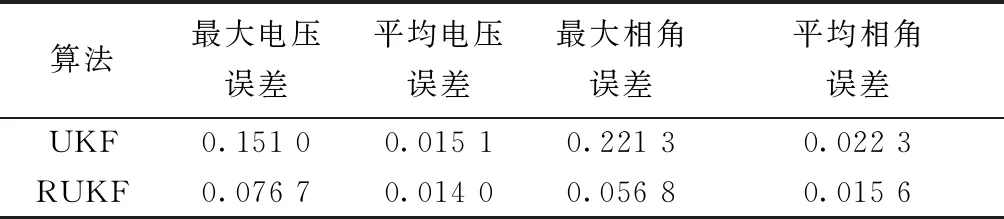
表1 IEEE33节点系统估计绝对误差对比Table 1 IEEE 33-bus system estimation absolute error comparison

图3 IEEE33节点系统估计结果和绝对误差Fig.3 IEEE 33-bus system estimates and absolute errors
从表1中的数据中来看,RUKF的电压最大绝对误差是UKF的35%,相角的最大绝对误差是UKF的22%,平均误差也都有所下降。从图3中也可以看出,在存在不良数据的情况下,UKF得出了与真值相差很大的平差结果,而RUKF并没有受到影响,平差结果更加贴近真值,绝对误差整体维持在一个较低的水平。
3.2 107节点系统
为验证RUKF算法在实际系统中的平差效果,使用某地市电网系统提供的日负荷功率及线路数据,选取一个变电站下的3条线路作为原型,系统模型如图4所示。
选取A20节点进行测量得到电压与相角的运行数据,并加入不良数据分别输入RUKF与UKF进行计算,仿真结果如图5所示,绝对误差对比如表2所示。
从表2中数据的绝对误差的最大值与平均值来看,RUKF平差效果整体优于UKF。RUKF的最大误差与平均误差都较UKF更低。不良数据虽不会引起滤波发散,但会导致估计精度下降。而且与IEEE 33-bus测试系统不同的是,本次实验中的负荷使用的是实际运行数据,电压与相角的波动较大,并不是维持在一个小范围内。在存在不良数据的情况下,UKF估计值的波动很大,并影响了后续的估计值,造成了残差污染,经过一段时间的稳定后绝对误差才回落至正常范围。而RUKF未受影响,在识别出不良数据后,使用伪量测值进行替代,保证了估计精度,估计值更贴近真值,平差效果较好。说明在实际应用中,当存在不良数据时,提出的RUKF与UKF相比,平差效果更好,且具有更高的稳定性与鲁棒性。可满足配电网数据平差需求。

图4 107节点系统模型Fig.4 107-bus system model

图5 107节点系统估计结果和绝对误差Fig.5 107-bus system estimates and absolute errors
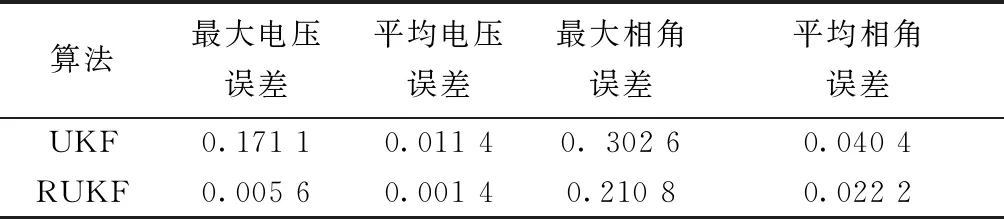
表2 107节点系统估计绝对误差对比Table 2 107-bus system estimation absolute error comparison
4 结论
提出了一种鲁棒无迹卡尔曼滤波数据平差方法,引入了运行模式的概念,给出阈值的计算方式与不良数据的检测标准,并在多个算例上进行了仿真验证。实验结果表明所提方法克服了传统平差算法中固定阈值会引发漏检或误检的缺点,有效地降低了不良数据对估计值的影响,提高了估计精度,比传统UKF具有更高的平差效果。
所提方法适用于处理配电网正常运行所产生的数据,根据数据变化趋势调整阈值大小,剔除其中的不良数据,但在配电网实际运行过程中,系统故障也会引起电压幅值与相角的跳变,其数据不具规律性,对于此情况RUKF可能会将前几个时刻的故障数据识别为不良数据,从而导致估计值延后,对故障反映较慢。
