承压水基坑变形稳定性因素影响分析

秦 羽, 李雄威, 刘正明, 肖金花

(1.常州大学环境与安全工程学院， 常州 213032； 2.常州工学院土木建筑工程学院， 常州 213032；3.江苏省地质矿产局第二地质大队， 常州 213300； 4.常州市轨道交通发展有限公司， 常州 213000)

轨道交通建设的快速发展使深基坑工程越来越受关注。基坑一旦发生事故，基坑围护结构将会产生较大的变形，将影响周边环境如邻近建筑物、道路、管线等的安全稳定，乃至形成严重的经济损失和人员伤亡[1]。地下承压水是造成基坑事故产生的关键原因之一，是基坑底部突涌的首要原因[2-3]。对基坑开挖现场监测的同时借助于数值计算的方法，能多方面更为精确地研究基坑工程整体变形[4]。Marsland[5]通过实验研究得出土体强度、基坑挖深、墙体入土深度等是影响临界水头关键要素的结论，同时可将其破坏模式分为整体顶升破坏、楔形体顶升破坏、表面砂沸破坏。宋建禹[6]对福州轨道交通2号线某承压水基坑抗突涌问题提出相关建议，结合数值分析与监测数据探讨基坑围护方案。由研究结果可知，对于不透水层较厚导致围护墙不易伸入承压水层的基坑，采用水下开挖的方式可有效预防基坑突涌事故、减小围护墙体的变形。丁春林等[7]以上海轨道交通M8号线承压水基坑工程为例，通过离心模型试验探讨该基坑不透水层存在与否、基坑挖深等对基坑的变形影响。由实验结果可知：无论不透水层存在与否，基坑挖深越大，对基坑变形影响越大；挖深较大时，不透水层缺失与否，造成的基坑变形差异较大。阳吉宝等[8]以苏州某广场基坑为研究背景，探讨承压水对基坑的变形影响，对基坑突涌问题进行验算并采取相关加固措施，对部分落深位置突涌稳定性问题的处理提出建议。夏春亮等[9]选取泰州市某水泵房基坑工程实例，采取数值分析的方式，探讨承压水基坑坑底加固对其稳定性的影响。可知，对比5种不同的加固措施，满堂加固更为有效地减小坑底土体的回弹隆起，其基坑抗突涌效果更显著。王晓楠等[10]就承压水基坑开挖围护结构内力与变形问题的研究成果进行了总结，说明了支护结构对周围土体的变形影响、支护结构内力计算方式、现场勘测的研究发展，并且讨论了现存的相关问题，为今后的研究做了铺垫。本文以常州地铁青枫公园站基坑工程为研究背景。通过建立基坑开挖数值计算模型，研究承压水作用下基坑变形及突涌稳定性状，对承压水降压幅度、不透水层厚度、围护墙入土深度等因素的抗突涌影响进行参数分析。

1 工程概况

本例基坑开挖过程中主要含水层为上层潜水和承压水。潜水层分布在填土层中，水位埋深在2 m左右，含水量小。承压水层为⑤1粉土层、⑤2砂土层以及⑧1粉黏土层，其中⑤1、⑤2层为1-1承压水层，⑧1层为1-2承压水层。采用地下连续墙施工后，⑤层承压水被截断，不会发生突涌，⑧1层承压水存在发生突涌的可能性，应予以重视。根据地质勘察报告、土体三轴试验、三轴加卸载试验、共振柱试验得到的土层参数见表1和表2。

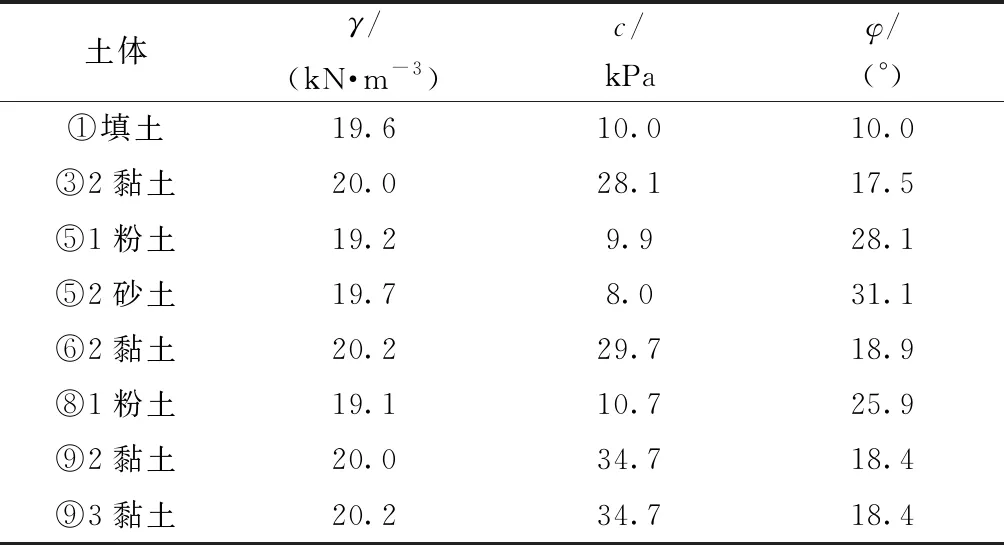
表1 土层基本参数Table 1 Basic parameters of soil mass

注：γ为重度；c为黏聚力；φ为内摩擦角。

表2 土体小应变模型参数Table 2 Soil small strain model parameters

2 基坑开挖的数值模拟与现场监测

本文采用的Plaxis大型岩土有限元软件是专门应用于岩土工程的数值模拟程序，内带多样土体本构模型。Plaxis软件工作流程主要包括：建模、网格划分、水力条件设置、工序输入、计算分析。该软件能很好地模拟岩土结构及施工工序，其计算结果相当准确，能考虑到土与结构间的作用。由于其强大准确的计算分析功能，在岩土方向研究领域应用较普遍。

2.1 数值计算模型

根据常州地铁2号线青枫公园站的实际开挖情况，采用Plaxis有限元软件模拟开挖过程中支护结构及其周围土体的变形。数值模拟计算中使用的土层参数是硬化土小应变(HSS)本构模型参数。依据工程地质调查报告和基坑围护结构设计图纸可知，基坑开挖宽度与深度分别为24、16.2 m，两边土层取到60 m的范围。基坑选用地下围护墙结合内支撑支护方案，地下围护墙深度达30.5 m、厚为0.8 m，沿墙体垂直方向设立3个支撑，第一个支撑采用混凝土支撑，第二个和第三个支撑采用钢支撑。在数值模拟中，地下连续墙由板单元模拟，内支撑由锚杆模拟，模型的边界条件使用固定位移边界及固定水头，土层与地连墙之间接触面的强度折损参数为0.75。如图1所示为数值模拟的该基坑开挖模型，空白处为开挖的基坑。围护及支撑材料参数如表3所示。

1为地下潜水的埋深；2为地下连续墙；3为第一道混凝土支撑；4为第二道钢支撑；5为第三道钢支撑图1 基坑开挖计算模型Fig.1 Foundation pit excavation model

表3 围护及支撑材料参数Table 3 Enclosure and support material parameters

注：EA为轴向刚度；EI为抗弯刚度；d为水平间距。

2.2 数值模拟结果

基坑开挖数值模拟过程与实际施工工况一致。数值计算结果收敛，达到预设的最终状态，基坑处于稳定状态未发生土体破坏现象。图2为数值模拟得到的围护结构及周边土体变形图，可知：

(1)基坑开挖时，墙体的水平变形值不断增大，随着墙体垂直方向呈现出先变大后减小的变化趋势，图2中墙体水平变形最大值为34.2 mm，位于地连墙深度的1/2左右(16.5 m)。

(2)基坑周围地面的最大竖向位移值为22.4 mm，在远离基坑边12 m附近，沉降值曲线表现为先变大后减小的“勺形”凹槽变形。

(3)从坑中央往基坑边土体隆起值逐渐减小，隆起值极值在基坑中间位置，其值为52.44 mm。

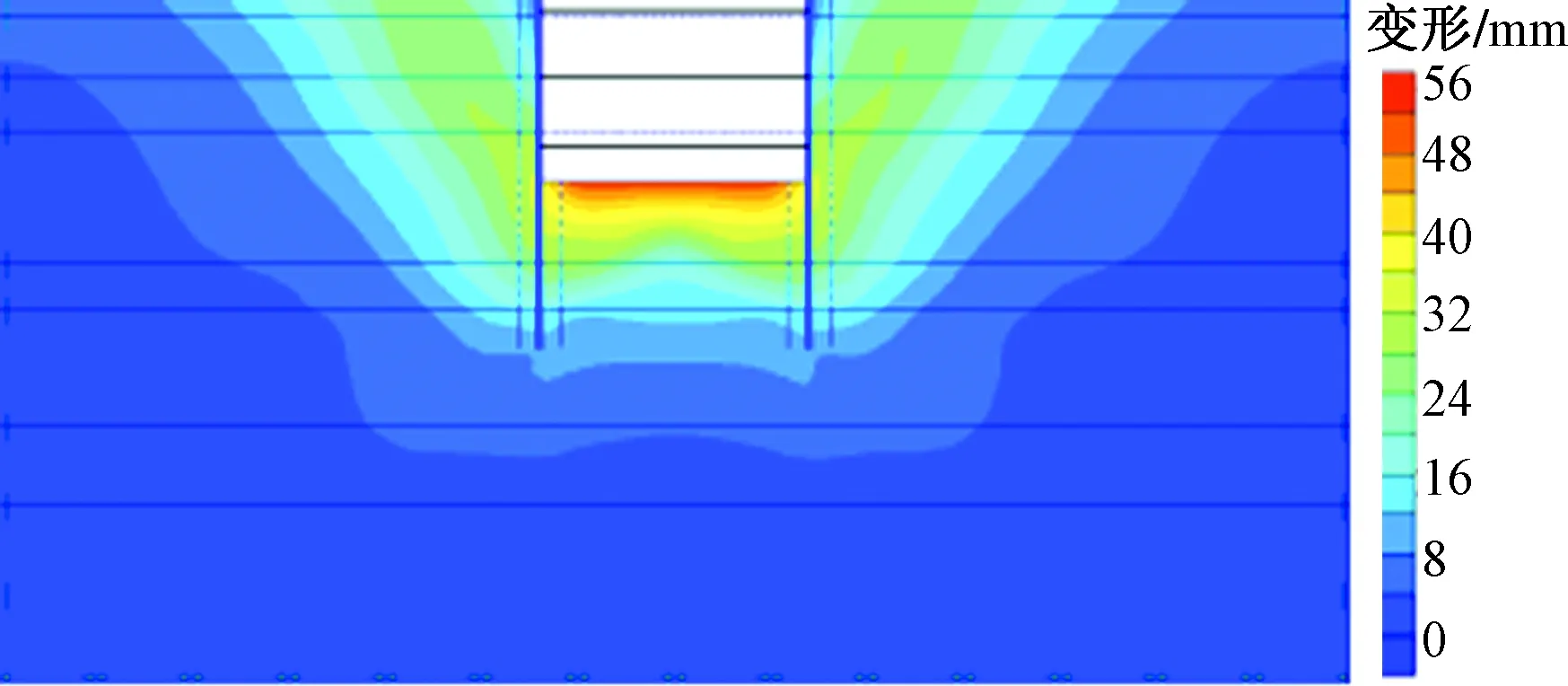
图2 数值模拟基坑开挖变形云图Fig.2 Numerical simulation of deformation nephogram of foundation pit excavation

2.3 数值模拟和现场监测的对比分析

施工现场地面沉降监测点设置按远离基坑方向的水平距离依次为2、5、5、10、10、15 m，围护墙水平变形监测点沿墙体竖直方向每隔0.5 m布置一个。墙体水平变形数值模拟结果，和最后一步开挖完成后墙体水平变形的计算值与实际监测结果比较分别如图3、图4所示。地表沉降数值计算曲线图、最终开挖步骤结束之后的地面沉降计算值和现场实测数据比较分别如图5、图6所示。

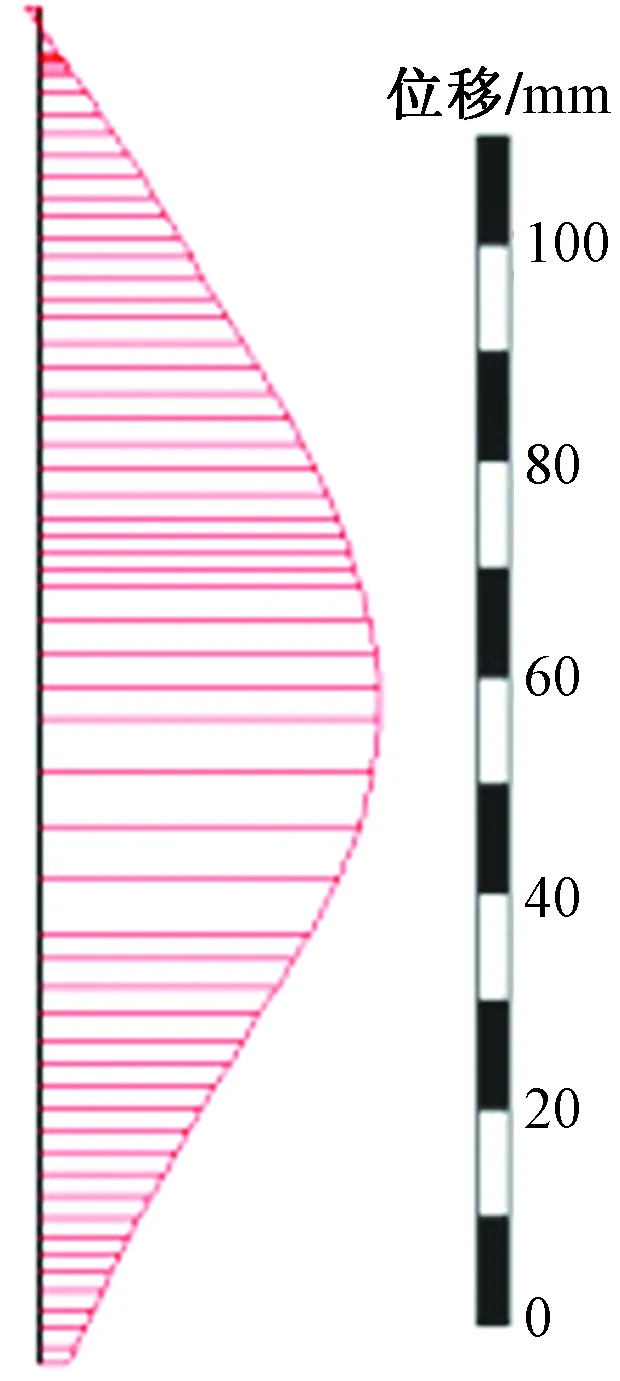
图3 地连墙水平位移计算值Fig.3 Calculated horizontal displacement of diaphragm wall

图4 地连墙水平位移计算值与现场监测值对比Fig.4 Comparison of calculated horizontal displacement of diaphragm wall with field monitoring value

图5 地表沉降计算值Fig.5 Calculated surface subsidence

图6 地面沉降计算值和现场监测值Fig.6 Ground settlement calculation value and on-site monitoring value

由图4可知：地连墙水平位移计算值和现场监测值的变化规律趋于一致，最大值分别为34.2、29.5 m，两者较接近，表明该深基坑采用的地连墙结合钢支撑支护体系设计是安全有效且利于基坑稳定，同时验证数值计算实际基坑开挖过程是合理的。由图6可知，地面沉降值的数值模拟值与监测数据的变化规律相吻合，两者都表现出先变大后变小的“凹槽形”分布形态。最大沉降值均出现在距基坑12 m左右的位置，分别为22.4、18.2 mm，沉降值最大的位置并不在基坑附近，而是位于基坑边一定距离处，主要原因是基坑周边围护结构与土体之间存在摩擦力等相互作用，减小了基坑周边土体的沉降。

3 基坑突涌模型的建立

3.1 基坑突涌的数值模拟

为了探讨⑧1承压水层对本项目基坑稳定性的影响，确定最终开挖深度为14、15、16 m等的基坑模型，分析基坑逐步开挖接近承压水层时不透水层土体的突涌稳定状态。实际模拟模型如图7所示。

1为地下潜水的埋深(2 m)；2为⑧1承压水层的水头高度(- 4 m)；3为地下连续墙；4为第一道混凝土支撑；5为第二道钢支撑；6为第三道钢支撑；7为最后一道基坑开挖线图7 基坑突涌的数值模型Fig.7 Numerical model of foundation pit inrush

在基坑开挖过程中，坑底土体的剪切应变往下部延伸，在不透水层底板即承压水层顶板处积累变大，土体隆起量较大。当开挖深度至17 m时，坑底土体隆起值为82.81 m，开挖至第四层土体时，数值计算不收敛，软件信息记载框显示“未达到预设的最终状态！土体破坏”。此时，隔水层底部与承压水层呈现脱离状态，坑底突涌应变状态如图8所示。

图8 基坑底部突涌应变机制Fig.8 Underflow strain mechanism at foundation pit bottom

从图8中可以看出，在第四步土层开挖过程中，基坑上方不透水层的土体重量不足以承受承压水的水压，并且在其与承压水之间产生裂缝，导致两层土之间发生脱离。由图8(a)可知，不透水层与承压水层交界处土体体积应变较大，在承压水压力的楔裂作用下基坑坑底顶升回弹，此时不透水层土体处于悬浮状态。由图8(b)可知土体剪切应变在地下连续墙内部的坑底较大，基坑不透水层土体隆起较大。可以看出，基坑的底部在楔形开裂和剪切的作用下产生顶升突涌破坏[10]。

3.2 承压水作用下的基坑稳定性

在实际工程防治中，通过管井降水降低承压水头的压力，提高基坑的稳定性，预防基坑突涌现象的发生。⑧1承压水层初始水头为-4 m，为了研究不同的承压水头下基坑开挖对周围环境的变形影响，本文建立了承压水头hw=-16、-12、-8、-4 m以及无承压水情况下的基坑开挖模型，探讨基坑开挖到坑底-17 m 时的基坑变形性状。如图9所示为各级承压水位下墙体水平变形数值计算结果。将每个级别水头压力下的围护墙体水平位移值与没有压力水头作用情况作对比，结果如图10所示，可知，没有承压水压力的墙体水平变形值较小，墙体的水平变形值与承压水头高度变化成正比关系，水头越高变形值越大。并且变形值最大的点深度在坑底附近，随着水头升高而降低，基坑稳定性随之下降。水头高度为-4 m时，墙体水平变形值比无承压水时增40.9%。

图9 各级水头高度下地连墙水平位移计算值Fig.9 Calculated values of horizontal displacement of diaphragm wall at different water head heights

图10 地连墙水平位移对比图Fig.10 Contrast diagram of wall horizontal displacement

4 抗突涌因素影响分析

前文总结了不同级别水头压力下的围护墙体水平位移值与没有压力水头作用情况的对比，以下将具体分析承压水降压幅度、不透水层厚度、围护墙入土深度等各参数对围护墙体最大水平位移的影响。为了便于结果分析，采用无量纲化的方法来表征基坑变形量，也就是说，根据围护墙最大水平变形值与开挖深度比(δhmax/H)的变化规律，分析了各种因素对基坑稳定性的影响。

4.1 承压水降压幅度的影响

承压水不同的降压幅度对应着不同的承压水头，前文建立了承压水头hw=-16、-12、-8、-4 m的基坑开挖模型，现用墙体变形无量纲化的方式分析承压水降压幅度对基坑稳定的影响，图11为第三步开挖结束(H=13 m)与开挖到坑底(H=17 m)的墙体无量纲化最大变形图。可以看出，围护墙体水平位移随着承压水头的升高呈现线性增大的趋势，且基坑开挖至坑底17 m 的水平位移与第三步开挖步相比明显比较大，可知承压水头越大，开挖深度越深，基坑越不稳定。降压前期较后期对基坑稳定性影响更显著，变化更明显。

图11 承压水降压幅度对δhmax的影响Fig.11 The influence of pressure drop range of confined water on δhmax

4.2 不透水层厚度的影响

研究不透水层厚度对基坑稳定性的影响，需要改变数值模型隔水层厚度值，设置承压水层顶板标高分别为-22、- 23 、…、- 27 m，对应的隔水层厚度分别为5、6、…、10 m。水头高度分别为-12、-8 m时的墙体无量纲化最大水平变形如图12所示。可知，墙体最大水平变形跟不透水层厚度是反比关系，隔水层厚度越薄，墙体变形越大，对基坑稳定性影响较大，反之，隔水层越厚基坑越稳定；承压水头越高，不透水层厚度对基坑稳定性影响越显著。工程中水头较高的基坑应保证足够厚的不透水层厚度，确保基坑稳定安全。

图12 不透水层厚度对δhmax的影响Fig.12 Influence of thickness of water-repellent layer on δhmax

4.3 围护墙入土深度的影响

工程中利用地连墙截断承压水与坑内土体的水力联系可以避免基坑事故的发生，本文研究围护墙不同入土深度对基坑变形稳定的影响。建立地连墙深度分别为30.5、32、33.5、35、5、38 m的基坑开挖模型，水头高度分别为-12、- 8 m时的墙体无量纲化最大水平变形如图13所示。可以看出，随着围护墙入土深度的增加墙体水平变形减小，当地连墙深度达到37.5 m截断承压水层时，墙体水平变形最小；曲线较平缓，说明围护墙入土深度对墙体变形影响不是很明显。工程中，承压水头较高，开挖深度较大的基坑可利用地连墙截断承压水层避免基坑突涌事故。

图13 围护墙入土深度δhmax对的影响Fig.13 The influence of the depth of the wall penetration on δhmax

5 结论

(1)基坑周围地表沉降、墙体水平变形数值计算结果与监测数据相吻合，说明数值模拟基坑开挖过程是合理的。承压水基坑稳定性随着水头高度升高、开挖深度增加而降低，本例基坑工程未进行降水的情况下即水头高度为-4 m时，开挖深度达到17 m基坑发生整体顶升突涌破坏。

(2)承压水条件下基坑开挖易发生突涌破坏，抗突涌影响因素包括：围护墙入土深度、不透水层厚度、承压水降压幅度等，基坑开挖过程中降低水头高度、增加不透水层厚度以及加深围护墙入土深度等措施可以提高基坑稳定性，预防基坑突涌破坏，减小围护墙水平变形，保护周围环境；承压水头较高的情况下不透水层厚度对基坑稳定性影响较显著，地连墙入土深度较其他因素对基坑稳定变形影响较小。