误差为空间自相关的空间自回归模型的主成分估计*

2020-12-15唐莹莹

广西民族大学学报(自然科学版) 2020年3期

关键词：共线性矩阵变量

唐莹莹

(广西师范大学数学与统计学院,广西桂林 541006)

0 引言

空间计量经济学是计量经济学的一个分支,以空间经济理论和地理空间数据为基础,以建立、检验和运用计量经济模型为核心,运用经济活动的空间自相关和空间不均匀性问题进行定量分析,研究空间经济活动或经济关系数量规律的一门经济学学科.

具有空间自回归的SAR模型是最常用的也是最为基础的模型,它通过空间加权矩阵将空间因素对经济现象的影响模式引入到模型中,且在被解释变量中存在空间相关性,这为模型的估计和检验带来了新的问题.

近年来,空间计量理论快速发展出现了误差为空间自相关的空间自回归模型,SARAR模型是一个存在混合的空间联合模型,同时考虑了被解释变量和误差项的空间相关问题:

这个模型因Clif和Ord(1973,1981)的两篇具有重要影响的文章而名,Anselin和Florax(1995)将其记为空间自相关误差自相关(spatial autoregressive model with autogressive ditubances,SARAR)模型.当ρ=0时模型变成空间误差模型(SEM),当λ=0时模型为空间自回归模型(SAR);当ρ=0且λ=0时,为线性回归模型.

在进行实际的空间计量模型拟合时,解释变量之间完全不相关的情况很少见,因为问题本身的复杂性和涉及的因素可能比较多,很难在众多解释变量中找出一组互不相关又对被解释变量有显著影响的变量,不可避免地会出现所选解释变量之间相关的情况.虽然多重共线性不影响系数的点估计,但会放大系数估计的方差,从而会导致降低的是参数估计的显著性,更容易得到不显著的结果;或者模型系数的符号可能有误,与实际不符合;或者参数估计值的置信区间也变宽,难于评估各个解释变量对被解释变量的影响.在SARAR模型中,由于误差为空间自相关而且因变量也为空间自回归,所以自变量之间存在的多重共线性问题还会使得自变量对因变量的解释产生干扰.

赵宇(2018)运用主成分估计去消除空间自回归中自变量的多重共线性;[1]曹芳(2012)运用Lasso方法处理多元线性回归的共线性问题;[2]郭双(2015)对SAR模型通过ALasso方法筛选出不显著的变量;[3]张元庆和陶志鹏(2016)对SAC模型变量选择进行了贝叶斯准则的研究;[4]Lee(2004)阐述了SAR模型的极大似然估计量所具体的性质.

本文将解释变量进行正交转换为若干个互不相关的主成分,建立起被解释变量对k个主成分作为新解释变量,结合极大似然方法估计出SARAR模型关系,再利用关系式β=Φ1α1将k个主成分的参数转换成原解释变量的新参数,去减少在有限样本中减弱多重共线性对参数估计的影响.

主成分特征提取方法主要是通过降维去除自变量压缩消除冗余.自变量们进行一个线性变换便得到线性无关的主成分,PCi=h1X1+h2X2+…+hnXn,其中hj是第j维度在第i个PC中的权重.首先找出总方差最大的PC,再找与第1个PC线性无关的而且能解释最多方差的第2个PC,直到取得所有的n个PC.原先的n个维度通过线性变换,变成了新的n个线性无关的按方差解释度排序的PC,最后根据累积解释程度选取所需的PC.

空间计量经济模型参数的常用估计方法极大似然估计法的基本原理是:假定误差项服从正态分布,继而可推导因变量的联合密度函数,再通过最大化对数似然函数得到模型的估计参数.Ord(1975)对空间滞后模型和空间误差模型的极大似然估计法进行了概述,而 Anselin(1988)则在 Ord(1975)、Bates和White(1985)研究基础上,进步推导了空间计量经济模型极大似然估计法和正则条件.

本文第一节简单介绍了SARAR模型和在多重共线性的危害下提出所研究的问题,第二节给出了所采用方法的参数估计推导,第三节和第四节同时通过大量的模拟实验去验证该方法具有有效性.

1 主成分对SARAR模型的参数估计

设Y为n×1阶因变量,X是一个n×p阶外生解释变量矩阵,ε～N(0,σ2In),

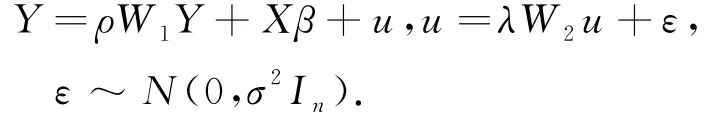
其中ρ和λ表示空间因素对其中研究对象的影响程度,β为对应p×1维自变量的参数向量.两种空间加权矩阵W1和W2是n×n阶的外生的空间权重矩阵,两者可以相同也可以不相同;分别表示空间因素对研究对象的影响,W1Y为空间滞后效应,W2u为空间误差效应.In为n阶单位矩阵.

将SARAR模型(2)做如下变形:

其中,中心化的X的相关系数矩阵为XTX,设其特征根为λ1≥λ2≥…≥λp,XTX的标准化正交特征向量为p×p维的矩阵ΦT=(ϕ1,ϕ2,…ϕp),ΦΦT=Ip且ΦTXTXΦ=qTq=Λ,其中Λ=diag(λ1,λ2,…,λp);令q=XΦ,α=ΦTβ;由(3)得到:

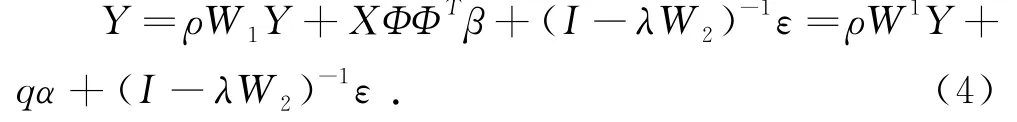
则可以将原模型可写成:

假设随机误差项ε～N(0,σ2In),参数集为θ=(αT1,ρ,λ,σ2);

模型(4)的对数似然函数为:

将(ρ,λ)和(ρ,λ)代入到lnL n(θ)得到最大化的中心化对数似然函数:

2 数值模拟研究

通过Monte carlo模拟在不同的参数和情况下对模拟和效果进行比对.

设定W1和W2为相同的“rook”形式空间权重矩阵;取ρ=0.8,λ=0.5,^σ2=1;对于初始值β分别取三组不同的值:

(1)β1=(3,2.5,0,0,0)';

(2)β2=(3,2.5,10,2.5,3)';

(3)β3=(3,0,10,0,3)';

设定样本数分别为225,400个,用于探究不同样本量下的结果;每次情况模拟次数为1000次.其中,采用Box和Muller(1958年)给出了由均匀分布的随机变量生成正态分布的随机变量的算法生成标准正态伪随机数,再用Mc Donald和Galerneau(1975)的自变量生成方法产生具有多重共线性的变量x ij=.再者r的取值为0.99和0.999以保证生成的自变量是存在不同的多重共线性并以研究其在不同共线程度对模型的影响程度.

表中的βML是在原数据构建SARAR模型的基础上直接应用极大似然估计方法估计出来的参数值,βPAC是对自变量进行主成分特征提取的基础上利用极大似然估计方法得到的参数值.

表1 r=0.99时所求参数的均方误差Tab.1 Mean square error of the required parameters when r=0.99

表2 r=0.999时所求参数的均方误差Tab.2 Mean square error of the required parameters when r=0.999

通过对比表1和表2中呈现的参数均方误差可以发现,当r=0.99时,EMSE(βML)与EMSE(βPAC)之间的没有很大的差距;但当r=0.999时,高度的多重共线性使得在直接使用ML方法估计出来的参数值与真实值有很大的误差,而在自变量进行主成分特征提取后再进行ML方法的参数均方误差要优于前者.

3 实例验证

本数据取自于Harrison和Rubinfeld(1978)收集的波士顿房价数据,并由Gilley和Pace(1996)加以完善.数据中包含506个波士顿普查区的中心数房价以及可以潜在决定房价的20个解释变量,选取业主自用住宅的价值平均数MEDV为被解释变量,TAX、LSTAT、PTRATIO、log(CRIM)、RM 为解释变量;W为506个区之间的“rook”形式空间权重矩阵,现构造如下的SARAR(1,1)模型:

首先对5个解释变量数据进行中心化处理,并计算相关系数.建立这5个解释变量的SARAR(1,1)方程,使用一般的极大似然估计的参数结果为βML.观察到log(CRIM)的系数值为0.0821355且其P值大于0.05,根据直观诊断法,log(CRIM)的系数可能有误,与实际不符.在该模型中,由于解释变量存在多重共线性会导致参数的解读和显著性并不理想.下面采用主成分估计对原解释变量进行转化.解释变量的相关系数矩阵如下: