无穷小数列的比式判别法与根式判别法*
2020-12-15何桂添李海玲唐国吉
何桂添,李海玲,唐国吉
(广西民族大学 数学与物理学院,广西 南宁530006)
0 引言
敛散性是数列的基本性质,收敛于0的数列称为无穷小数列(发散于∞或+∞,-∞的数列称为无穷大数列).无穷小数列在收敛数列中扮演重要的角色,它对于研究数项级数的敛散性起着基础性的作用.通行的数学分析教科书(文[1,3,5]等)都用专门的章节介绍数列的收敛性(包括极限的存在性与计算),主要的方法有定义法,柯西收敛准则,单调有界定理,两边夹定理等.我们知道,研究一般数列收敛性的方法都可以用来研究无穷小数列.然而,我们发现,对于无穷小数列的介绍和研究还不深入.另一方面,数学分析教科书(文[2,4,5]等)都介绍了正项级数收敛性的比式判别法与根式判别法.
受以上文献的启发,在本文中我们提出判别无穷小数列的比式判别法与根式判别法.顺带地,得到判别无穷大数列的相应判别法,给出例子说明主要结果.
在结束本节之前,我们先回顾几个基本的结果(如分别参见文[2]第29页练习题9和练习题8).

1 比式判别法

即当n>N时,有an+1 注1:q=1时,数列{an}可能是无穷小数列,可能是发散数列,也可能是收敛于任意指定正数的收敛数列.例如考虑3个数列:;(ii){n};(iii)任意指定的正数t,常数列{t}.容易验证这3个数列都满足是无穷小数列;{n}是发散数列;对任意给定的正数t,常数列{t}收敛于t.故当q=1时,无法鉴别数列{an}是否为无穷小量. 证明 :由定理1和引理2可推得结论. 若定理1和推论1中极限不存在时,可考虑上极限和下极限来判断. 我们先给出比式极限与根式极限的关系. 定理3 设数列{an}满足条件an>0,∀n∈ 注3:由定理3的前半部分知,凡是能由比式判别法鉴别的无穷小数列,也能由根式判别法来判断,再结合定理3的后半部分知,根式判别法适用范围较之比较判别法更广泛. 众所周知,当公比q满足|q|<1时,等比数列{qn}是无穷小数列.从定理1和定理2的证明可以看出:比式判别法和根式判别法都是借助于两边夹定理与一个无穷小的等比数列做比较来实现的.换句话说,只有当一个无穷小数列收敛于0的速度比某个无穷小的等比数列快时,才可以用比式判别法和根式判别法来判别.加深对无穷小数列的认识有利于对数项级数收敛性的研究.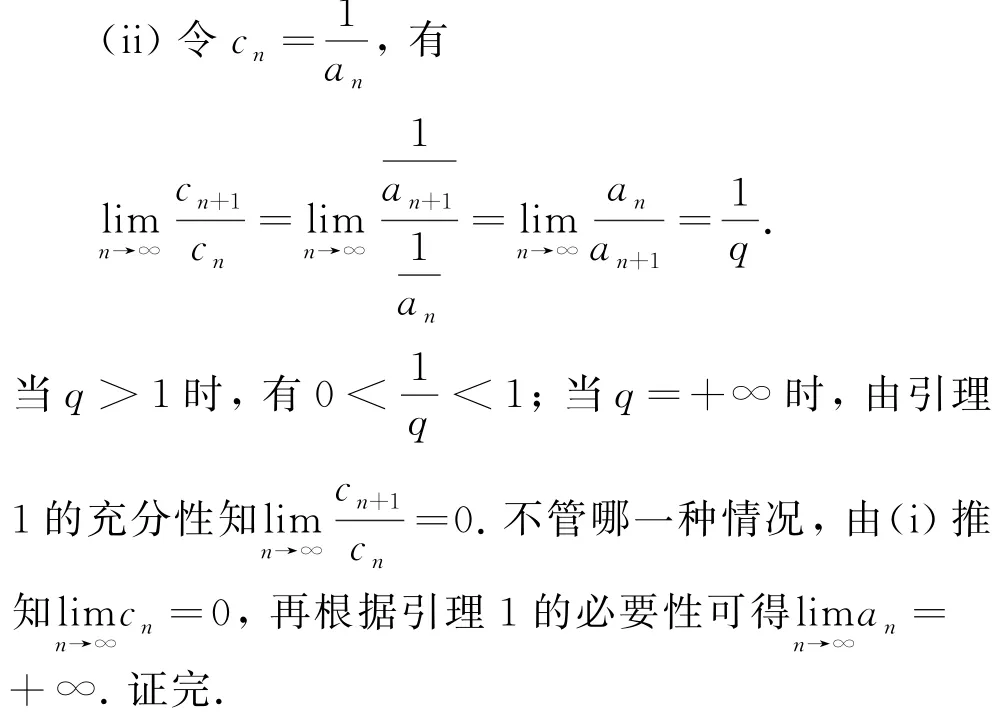


2 根式判别法



3 结论

