基于内聚力模型的沥青混凝土-无机结合料层间剪切试验数值模拟
2020-12-15张敏江
张敏江, 于 江*, 郭 超
(1.沈阳建筑大学交通工程学院, 沈阳 110168; 2.沈阳建筑大学土木工程学院, 沈阳 110168)
无机结合料稳定类基层在高等级公路中广泛应用[1]。无机结合料稳定类基层和沥青混凝土面层间材料的差异,会使基面层层间连接状况较差,由此导致路面推移和疲劳开裂等病害,严重影响沥青路面的路用性能和使用寿命[2]。
对于沥青路面连接层力学特性,中外学者进行了大量研究。张丽萍等[3]研究了应用4种不同基面层间的连接层时无机结合料稳定层的疲劳开裂寿命,并用摩擦系数描述4种不同连接层的连接能力。结果表明连接层的连接能力越强,沥青路面的疲劳寿命越大;Chun等[4]通过面层与基层间设置弹簧单元的数值模型,分析车辆荷载下路面的疲劳特性,结果表明:良好的层间连接可以改善路面的受力状态,延长路面的使用寿命;姜利等[5]分析了不同降温条件、连接层厚度及模量对温度应力的影响,并用实体单元描述路面面层与基层间的连接层。结果表明温度幅度越大,应力集中现象越明显,连接层刚度越大,温度应力越大。李彦伟等[6-7]基于分层失效理论分析了固定位置荷载对带有连接层的路面结构影响。周晓和等[8]考虑了连接层的初始损伤的影响。
以上学者关于路面层间行为的研究或只考虑了路面连接层的黏结力,未考虑层间的摩擦力,或只考虑了层间的摩擦力,未考虑连接层的黏结力。真实的路面结构在行车荷载作用时,荷载正下方的层间位置即受剪也受压,此时层间的抗滑移能力由摩擦力与层间材料的黏结力共同提供,故数值计算有必要充分考虑连接层的黏结力与层间摩擦力的作用。针对以上问题,提出一种考虑摩擦的内聚力模型描述层间行为,首先对沥青混凝土-无机结合料稳定类材料复合试件进行直接剪切试验,分析压-剪耦合受力状态下复合试件的剪切力与加载位移之间的关系,确定连接层的黏结力与摩擦系数。然后,根据试验结果拟定包含摩擦效果的Park、Paulino、Roesler内聚力模型(简称PPR内聚力模型)的层间连接本构参数。最后通过数值模拟结果与实验结果的对比分析,验证PPR内聚力模型描述路面结构层间行为的合理性与可行性,为今后关于沥青路面层间行为方面的研究提供参考。
1 直接剪切试验
研究的层间连接材料选用稀浆封层,并通过调整法向荷载的大小,测量不同法向荷载下复合试件的抗剪强度,获得剪切位移-剪切应力曲线,并根据摩尔-库伦理论拟合法向荷载-抗剪强度曲线,标定层间材料的黏结力与摩擦系数。
试验试件如图1所示。剪切试验示意图如图2所示。平衡方程如下:

图1 稀浆封层复合试件

图2 直接剪切试验加载模型
μIp+c=τmax
(1)
式(1)中:μ为摩擦系数;Ip为层间接触压应力,MPa;τmax为试件的抗剪强度,MPa;c为层间材料的黏合力。
设τ为层间剪切应力,当τ<τmax时,τ一直处于应力强化阶段;当τ>τmax时,层间材料的黏合力下降,τ随剪切位移的增大而降低,处于应力软化阶段。摩擦系数根据直接剪切试验所得。
试验首先设定竖向荷载为Iσ,然后施加水平位移荷载。当水平位移荷载形成的水平剪应力达到试件最大抗剪强度时,水平加载力为Ir,根据式(2)、式(3)计算剪切面上的接触压应力Ip和抗剪强度τmax[9-10]:
(2)
式(2)中:Sv为垂向油缸活塞面积,m2;G为滚珠轴承、传力铁板及上层沥青块的总重,MN;Si为剪切面面积,m2。
(3)
式(3)中:Sh为水平油缸活塞面积,m2。改变垂直荷载大小,得到不同正应力下对应的抗剪强度,利用最小二乘法计算得到下封层材料的摩擦系数μ。
根据直接剪切试验及式(1)、式(2)计算得到的法向荷载-剪切强度关系曲线如图3所示。

图3 法向荷载-剪切强度关系曲线
根据图3可知,用最小二乘法将法向荷载与剪切强度拟合成线性关系,根据摩尔-库仑定律测得层间材料的黏结力为0.075 1 MPa,摩擦系数为0.504。
2 直剪试验的数值模拟
2.1 PPR内聚力模型
为了更加全面地体现路面结构层间的黏结力与摩擦对层间滑移行为的影响,采用PPR内聚力模型。在2009年Park, Paulino, Roesler等[11]提出PPR内聚力模型,该模型每个参数都有明确的物理意义,而且黏结力及切线刚度矩阵由连续势能函数统一控制,分别对势能函数求法向、切向位移的一阶微分可得到法向与切向内聚力Tn与Tt,对势能函数求二阶微分可得到层间材料的雅可比矩阵。由于势能函数对位移的二阶可导性,可知内聚力-位移曲线是一个连续光滑的曲线,故计算模型数值迭代的可收敛性得到了提高[12-13]。
PPR内聚力模型的势能函数如下:

(4)
式(4)中:Δn与Δt分别为法向与切向张开位移;φn与φt分别为法向与切向的断裂能;α与β分别为控制达到剪切强度后法向与切向内聚力的软化形式的参数;Γn与Γt为法向与切向的断裂能常数;m、n为无量纲常数。势能函数被控制在一个作用域之中,作用域的边界为(0,δn)、(-δt,δt),δn与δt分别为法向与切向的最终张开位移,δn与δt由式(5)给出。
(5)
式(5)中:σmax与τmax分别为层间材料法向与切向的强度,也是内聚力所能达到的最大值;λn与λt分别控制内聚力-位移曲线的初始刚度,数值上等于内聚力达到的最大值时的位移与势能函数作用域边界的比值,控制方程为
Tn=(λnδn,0)=σmax,Tt=(0,λtδt)=τmax
(6)
Tn与Tt随张开位移的变化关系为
(7)
Γn与Γt为法向与切向断裂能的函数,当法向与切向断裂能不相等时,断裂能常数为
(8)
当法向与切向断裂能相等时,断裂能常数为
(9)
式(9)中:m、n由α、β、λn、λt控制,m、n的计算方法为
(10)
由以上内容可知,PPR内聚力模型共需要用户输入8个参数,它们分别为断裂能φn、φt,强度σmax、τmax,初始刚度控制参数λn、λt,软化形式控制参数α,β。根据上述位移-牵引力关系,绘制PPR内聚力模型中内聚力与位移的关系,如图4所示 (φn=φt=1 MPa·mm,σmax=τmax=1 MPa,λn=λt=0.4,α=β=4)。

图4 PPR模型位移-内聚力关系
由图4可知,PPR内聚力模型的法向内聚力既受法向位移的影响,又受切向位移的影响,其切向内聚力同样受法向与切向位移的共同影响,内聚力随位移的改变而连续柔顺地改变。
2.2 摩擦行为的描述
Tvergaard[14]在1990年提出考虑摩擦的内聚力模型,该模型假设层间内聚力降为0后摩擦力起作用,这会导致内聚力与摩擦力的转换不光滑,造成计算收敛困难。为了解决上述问题, 2015年Spring等[13]提出一种在内聚力达到峰值时出现层间摩擦的PPR模型,虽然该模型充分考虑了摩擦系数与内聚力对抗剪强度的影响,但是当摩擦力过大时,会出现剪应力峰值滞后的现象,这是因为该模型中内聚力的峰值与摩擦力的峰值不处于相同大小的剪切位移,导致了该模型不能充分体现材料内聚力与层间摩擦力共同提供的抗剪强度。在路面结构中,通常根据摩尔-库仑强度理论(τ=c+σtanφ)确定路面层间的抗剪强度,所以应使层间材料内聚力的峰值与摩擦力的峰值出现在相同的剪切位移。
鉴于此,提出了一种新的计算摩擦的PPR内聚力模型,在该模型中,摩擦力与内聚力的耦合关系为
(11)

当界面两侧的单元被挤压而相互侵入时,界面内会产生抵抗力,抵抗力的大小取决于单元侵入的深度和界面受压状态时的法向刚度,受压时法向刚度恒等于受拉位移趋近于0时的法向刚度。模型假设当界面受压且层间出现剪切滑移时会产生摩擦力,之后随着剪切位移的增大柔顺光滑地增大,具体增大方式为
Tf=μκ(Δt)|Tn|,Tn<0且Δt>0
(12)
式(12)中:μ为层间摩擦系数;κ为一个随剪切位移增大而由0单调且连续增大至1的参数,κ的表达式为
(13)
式(13)中:s为控制摩擦力增长方式的转化形态参数,s对κ的影响如图5(a)所示,因此该模型可以确保内聚力峰值与摩擦力峰值出现在相同的剪切位移,并且内聚力与摩擦力之间可以柔顺转化。Tt(0,Δt)为法向位移为0时切向内聚力,表达式为

(14)
式(14)中:考虑摩擦效果的PPR内聚力模型需用户输入与2.1节中意义相同的8个参数,分别为Γn、Γt、σmax、τmax、λn、λt、α、β,除此之外还应输入摩擦力增长形态参数s和层间摩擦系数μ。绘制的内聚力与摩擦力耦合关系曲线示例如图5(b)所示。

图5 不考虑摩擦的切向内聚力与摩擦力的耦合方法
将上述理论引入ABAQUS展开有限元分析,由于ABAQUS隐式算法需要用户给出材料的雅克比矩阵D,其分量形式如式(15)所示。对势能函数求位移的二阶微分即可获得材料各方向的切线刚度,内聚力与摩擦力耦合的材料刚度计算方法[15]为
(15)
式(15)中:


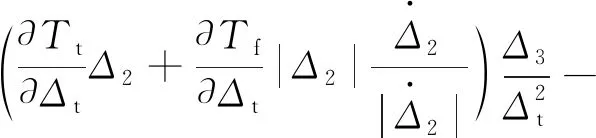

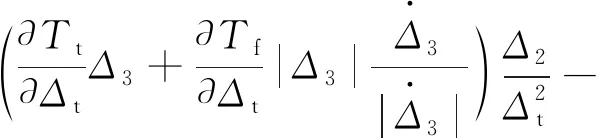




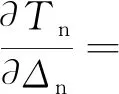
(16)

(17)

(18)
(19)
提出的摩擦力部分的刚度为
(20)
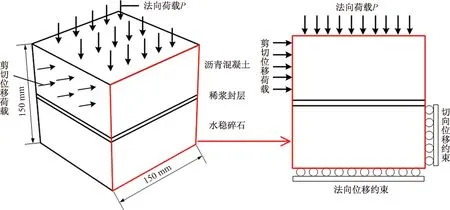
图6 数值模型的尺寸、边界条件和荷载工况
3 数值计算与验证分析
在数值计算中,模型的尺寸与直剪试验试件的尺寸相同,其整体为一个150 mm×150 mm×150 mm的正方体,分为上下两层,分别是沥青混凝土层与无机结合料层,其厚度均为75 mm,两结构层均选用8节点实体单元(C3D8),位于两层中间的是连接材料层,在数值模型中由一层零厚度的单元表征,采用UEL(用户自定义单元子程序)将考虑摩擦的PPR内聚力本构模型嵌入到零厚度单元。在试件模型的顶部施加不同大小的法向荷载,在沥青混凝土层的侧向施加剪切位移荷载,在模型的底部施加法向位移约束,在与剪切位移荷载对侧的无机结合料层的侧向施加切向位移约束。数值模型的具体尺寸、边界条件和荷载工况如图6所示。数值模型的计算分为两步,第一步施加边界条件与法向荷载,第二步施加剪切位移荷载。
由于主要研究沥青混凝土与无机结合料之间的层间行为,故假设沥青混凝土与无机结合料均为理想弹性体,沥青混凝土的弹性模量与泊松比分别设为1 200 MPa、0.3,水泥稳定碎石的弹性模量与泊松比分别设为1 800 MPa、0.25。参考考虑摩擦的PPR内聚力模型,并根据直接剪切实验结果与界面间I、II型裂缝断裂能的物理意义,计算不同层间材料的力学参数[16],具体参数信息如表1所示。

表1 稀浆封层力学参数
其中层间材料的强度与剪切试验过程中的剪切应力峰值相等,断裂能取为无法向荷载的剪切试验测得的剪切位移-剪切应力关系曲线中剪切应力与剪切位移围成的图形的面积。λn与λt取为实验剪切过程中达到剪切应力峰值时的剪切位移与层间材料受剪失效时的剪切位移的比值。α、β与s根据剪切位移-剪切应力关系曲线的形状估测,μ为层间摩擦系数。基于考虑摩擦效果的PPR内聚力模型,综合考虑了法向荷载、断裂能、强度和摩擦系数等因素的影响,数值模型的计算结果如图7所示。

图7 数值模型的剪切位移-剪切应力曲线
基于考虑摩擦效果的PPR内聚力模型可以对试件剪切滑移的全过程进行模拟,在法向荷载分别为0、0.1、0.2、0.3、0.4 MPa时,复合试件的抗剪强度分别为0.074、0.125、0.174、0.224、0.274 MPa。可见随着压应力的增大,试件模型的抗剪强度也会线性增大。观察图7可见,在剪切位移刚开始时剪切应力会接近线性的增大,此时内聚力与摩擦力都处于增大阶段,在临近剪切强度时增大趋势逐渐放缓,达到最大值之后,剪切位移的增加会导致剪切应力下降,此时摩擦力保持恒定不变,内聚力逐渐减小。当法向荷载为0时,剪切应力最终会下降至0,因为没有法向荷载就不会产生摩擦力,当法向荷载不为0时,剪切应力最后会有残余部分,该残余部分完全由摩擦力提供。
提取数值模型中法向荷载与剪切强度,并对其线性插值,可以得到法向荷载-剪切强度关系曲线,并将其与实验结果对比,如图8所示。
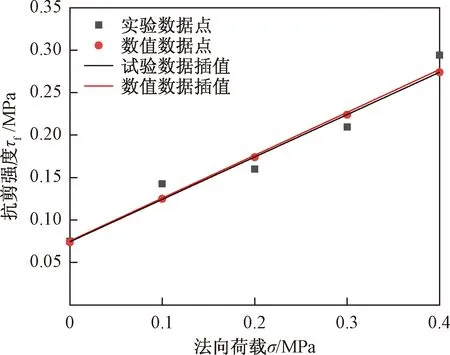
图8 法向荷载-剪切强度关系曲线
由图8可知,对试验及数值计算获得的荷载-剪切强度数据点进行线性插值,插值结果显示两曲线重合度较高,证明考虑摩擦的PPR内聚力模型对不同法向荷载工况下复合试件剪切强度预测具有较高的准确性。
对比有与没有法向荷载两种工况下(P=0.1 MPa,P=0)试验及数值模型获得的剪切位移-剪切应力曲线,如图9所示。

图9 试验与数值结果的剪切位移-剪切应力关系曲线
由图9可知,数值模型计算得到的剪切位移-剪切应力关系曲线与试验的结果基本一致,证明该种考虑摩擦效果的PPR内聚力模型能够较为准确地描述受与不受法向压力工况下施加剪切位移荷载时复合试件的受力变形特点。在法向荷载为0.1 MPa的工况中实验所得的最大剪切应力稍大于数值计算所得的最大剪切应力,其原因主要是数值模型的层间材料的断裂能与抗剪强度是根据法向荷载为0工况时剪切位移-剪切应力关系曲线计算所得,而试件制作过程不能保证试件与试件的层间黏合情况完全一致,黏合情况的细微不同会导致实验结果与数值结果的较小差异。在试验中,当层间材料完全失效时,沥青混凝土与无机结合料表面会产生一定程度的破损及石料剥落,这会导致剪切位移-剪切应力关系曲线最后的纯摩擦阶段出现跳跃与不平稳的情况。
4 结论
(1)对复合试件进行直接剪切试验,结果表明法向荷载越大,复合试件的抗剪强度越大。用最小二乘法对实验所得数据线性插值,可以得出稀浆封层的黏结强度为0.075 1,层间的摩擦系数为0.504,表明此种方法可以为测量其他沥青路面层间材料的抗剪强度与摩擦系数提供依据。
(2)对受法向压力荷载的复合试件施加剪切位移荷载得到的剪切位移-剪切应力关系曲线可以分为3个阶段,分别为:①剪切应力强化阶段,此阶段摩擦力与内聚力均随着剪切位移的增大而增大;②剪切应力软化阶段,此阶段摩擦力保持不变,内聚力下降;③残余剪切应力阶段,此阶段的剪切应力主要来自层间的摩擦力。
(3)提出的考虑层间摩擦效果的PPR模型中,摩擦力及其与内聚力之间可以随剪切位移的增大而柔顺变化。此外,该模型确保黏结力最大值与摩擦力最大值出现在同一剪切位移处,所以该模型可以充分体现层间材料的黏结力与摩擦力对复合试件抗剪强度的影响。
(4)数值模型计算得到的各种法向荷载工况下复合试件的抗剪强度与实验测得的强度较为相近。对比是否考虑法向荷载作用下,数值模型及试验所得的剪切位移-剪切应力关系曲线,可知实验曲线与数值模型曲线基本吻合。证明该种考虑摩擦的PPR内聚力模型能够较为准确地预测受压状态下复合试件的抗剪强度,也能较为准确地描述受与不受法向压力工况下施加剪切位移荷载时复合试件的受力变形特点。在涉及层间行为的路面结构计算中此模型具有一定的合理性,为类似复合结构的剪切行为问题的研究提供依据。
