云南大理复杂地形上风场的模拟研究
2020-12-15周晓鸥于潇萌孔维奇张其林
周晓鸥, 曹 乐, 于潇萌, 孔维奇, 张其林
(南京信息工程大学大气物理学院, 南京 210044)
大风是云南地区的灾害性天气之一,给人民生命财产带来重大损失。由于云南地区地处低纬度高原,地形地貌复杂多样,更有超过80%的面积为山地,所以云南微气象、微地形条件下风害的形成机理、变化规律与台风、龙卷风等不同,具有明显的地域特征,即受地形影响较大。复杂的云南地形致使局部环流、“狭管效应”明显。因此,云南地区时常因风害造成输电线路的运行故障,跳闸频发,给人民生产生活带来极大不便。因此研究云南地区特殊复杂地形上大风的天气规律,对预报大风天气具有重大意义。
关于复杂地形上的大风天气,学者们的相关研究主要可分为数据统计分析、风洞实验研究以及数值模拟3类。
数据统计分析是通过收集大量的风场数据,并对其进行分析和概括总结。杨芳园等[1]对云南省的一次飑线大风天气进行了中尺度特征分析,第一次探究了地面大风天气与地面流场之间的关系,从而可提前1 h预报飑线。杨智等[2]采用涡动相关法分析了观测资料,探讨了大理近地层中湖陆风、峡谷风特征以及形成原因和影响因素,得到大理不稳定层结白天比夜间多,湍流白天多于夜间并随着风速的增大而减小的结论。徐安伦等[3]通过分析全球定位系统(global positioning system,GPS)探空加密观测资料,得到云南洱海湖滨区大气边界层厚度、位温、比湿、风速、风向等的垂直结构。其中风向在高层因受大尺度环流控制,以西风为主;中层气流则主要被地形影响,局地环流明显;而低层白天盛行东风和东南风,夜间多为西风和西南风。杨澄等[4-5]利用大理基本气象站1971—2010年地面观测的风资料并结合NCEP[6](National Centers for Environmental Prediction)高空风资料,分析了大理市大风日数的年变化、年代际变化、季变化、月变化、日变化以及大风风向和风速的特征。此外,还选取大理地区近年来5个冬季大风个例进行分析,讨论了导致青藏高原东南侧大风产生的环流背景和动力、热力因子。此外,学者们还对不同下垫面特性的大风天气时空分布特征进行了详细分析[7-10]。
风洞试验研究是按照各实物比例缩小,在地面人工环境中固定摆放研究物的模型,使用人造气流来模拟各种复杂地形上的风场。谯泽诊[11]利用风洞试验方法,对两种新式挡沙墙的挡风效果进行模拟实验研究,为大风区域防风防沙的工程措施提供评价支撑。赵爽等[12]和田连博等[13]分别以不同的大跨越输电塔体系为背景,通过分析气弹模型风洞试验,研究了导线与输电塔之间的关系。
数值模拟是利用计算机求解流体流动的各种守恒控制偏微分方程组的技术,从而模拟仿真实际的流体流动情况的一种方法。李致宇[14]在考虑大风和覆冰这两个因素对输电杆塔的影响下,提出了一种杆塔功能函数模型并进行了检验,对电力系统的安全运行具有重要意义。陈业国等[15]运用中尺度数值气象研究与预报(weather research and forecasting,WRF)模式[16]对一次华南强飑线过程进行了模拟研究,得出此次飑线过程的触发和维持机制。王澄海等[17]通过新一代WRF模式对新疆“2·28”大风过程进行了模拟分析,得出其触发机制不仅有地形和天气环流系统,还有大气的斜压性产生的垂直速度导致的高空动量的垂直输送,以及大风发生前地面的非绝热加热引起的感热和潜热通量的增加。同年,汤浩等[18]也对此次大风天气过程使用WRF模式进行模拟,表明新疆的特殊复杂地形和极大地气压梯度是造成此次大风的重要原因。罗啸宇等[19]运用 ANSYS/Fluent18.0对强台风“天鸽”中受损线路周边的风场进行了数值模拟,分析了输电线路附近复杂地形对风场的影响。Jubayer等[20]通过数值模拟与风洞试验相结合的方法,对复杂地形上的风速进行了估算。
关于近地层大风天气已有大量观测及模式的研究,但目前已有的研究多是针对平坦地形条件下的风场及其变化规律,对具有特殊微地形条件下的风场变化规律特别是局部大风形成机理却认识不足。因此,针对云南大理这一具有特殊地形的地区,对局地地形上的风场运用三维大涡模式OpenFOAM(open field operation and manipulation)[21]进行小尺度高分辨率数值模拟,从而获取该区域内风速风向的时空分布,分析研究近地层大风的形成和演变机理,以减少当地因风灾造成的各种电力故障及其产生的人民生命财产损失。
1 数据与方法
选取云南大理南的45~47号电线杆塔区域(云南大理南部)作为研究区域,中心观测点为 46号杆塔处(100.24°N,24.83°E)。首先将该研究区域的下垫面地形数据导入MATLAB、SOLIDWORKS、ANSYS ICEMCFD 等软件进行计算域的生成以及网格的划分;接着选用合适的次网格模型,从而得到较为精确的大气边界层内的湍流混合强度的空间分布;再将第二步所得到的湍流混合强度分布耦合到具有第一步所生成的边界形状的复杂计算域中的三维大涡模式OpenFOAM中,在添加适合复杂下垫面的壁面模型后进行数值计算。论文的数值计算得到南京信息工程大学高性能计算中心的计算支持和帮助。
1.1 复杂地形计算域及其网格的生成
网格质量决定了数值模拟的准确性,因此需要生成高质量网格来提高数值模拟的准确性。首先需得到经过自编MATLAB程序处理的计算区域的地形数据(地形数据来源于srtm数据[22],水平尺度约为3.6 km×3.6 km,选取区域的中心经纬度为100.24°N,24.83°E),将之作为散点群集导入三维机械设计系统SOLIDWORKS生成计算域下垫面[图1(a)],然后将生成的下垫面导入网格生成软件ANSYS ICEMCFD,在此下垫面基础上添加侧面和顶面。因大气边界层高度约为1 km,为充分考虑其湍流流动影响区域,将垂直方向上的高度设为 2 km,从而生成完整的计算域[图1(b)]。最后对该计算域进行网格划分,生成可应用在本研究的流场解算器OpenFOAM中的结构化网格。在水平方向上,计算域边界处的网格分辨率为45 m,中心加密处水平分辨率为30 m,而垂直分辨率为40 m。

图1 计算域下垫面及整体计算域及网格
1.2 三维大涡模拟中的次网格模型的选取
目前应用于湍流的数值模拟方法主要分为 3种:直接数值模拟(DNS)、雷诺平均方法(RANS)和大涡模拟(LES)。直接数值模拟(DNS)可以获得湍流场的精确信息,但现有的计算资源无法满足模拟需求。雷诺平均方法(RANS)可以计算高雷诺数的复杂流动,但该方法输出的是平均运动结果,不能反映流场的细节信息。而大涡模拟(LES)方法可以直接计算大尺度涡的运动,并且通过建立次网格模型来体现小尺度涡的运动对大尺度涡的运动的影响,因此该方法既可以得到较雷诺平均方法更多的动态信息,又比直接数值模拟计算量小,因此得到了越来越广泛的应用。研究中采用的即大涡模拟的方法,对大气边界层内的湍流混合强度进行计算。
在大涡模拟中,把湍流运动通过滤波方法分解成大尺度运动和小尺度运动两部分,大尺度运动可通过数值求解微分方程直接计算,而小尺度运动对大尺度运动的影响在运动方程中则表现为类似雷诺应力一样的应力项,此应力称为次网格雷诺应力,需要用次网格模型来模拟。目前,在大涡模拟中经常广泛采用的次网格模型有标准的Smagorinsky模型[23]、动态涡黏性模型、动态混合模型[24-26]等。其中Smagorinsky模型是第一个被广泛应用于大涡模拟中的次网格模型。在该次模型中,次网格应力的表达式为
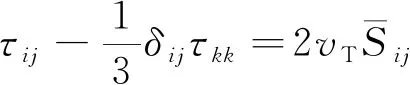
(1)
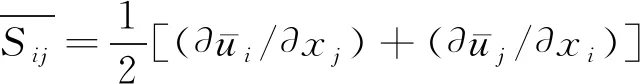
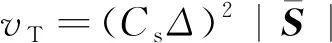
(2)
研究中采用的次网格模型相较于参数化方法,具有物理意义明确、精度高、健壮性好等特点,并在之前的关于大气边界层的大涡模拟研究中[27]已被证明了可以很好地计算边界层内的有效湍流黏性,因此可以满足研究边界层内湍流混合强度的计算精度要求。
1.3 三维大涡模拟的建立
使用开源软件OpenFOAM来求解三维Navier-Stokes方程组[28],从而来捕捉空气的流动以及各气象要素的时空分布。在运用三维模式OpenFOAM求解流场方程的过程中,使用1.1节中生成的具有复杂地形条件的计算域以及网格数据,对于湍流的处理则采用1.2节所述的次网格模型来计算流场中的有效湍流黏性。计算还需添加了可准确代表研究区域气象要素的初始场和边界场等信息。为研究不同风向条件下复杂地形对风场变化的影响,采取理想状态下的风向作为风速的初始入口边界场(东南西北4个风向)。因云南省年平均风速为2~3级(取平均值3 m/s),且大风天气的平均风速较少超过17 m/s,瞬时风速较少超过24.0 m/s[5],选取入口风速为3~30 m/s,每间隔3 m/s计算一个算例。根据《风力等级》(GB/T 28591—2012),每一级间隔约为3 m/s,4个风向共40个算例。由于目前该算例采用理想状态下的风速风向作为风速的边界场,且该计算在一段时间后达到稳定,因此目前输出7 200 s的计算时间。此外,在计算域的两侧和顶部施加对称边界条件,这意味着法向速度为零以及这些边界上的其他变量都为零梯度。在计算域的出口处,施加零静压。对于地面,还使用了适用于复杂地形的M-O(Monin-Obukhov)壁面模型[29]。
模式中处理近壁面区域通常有两种方法:一种是壁面函数法,即使用一种称之为壁面函数(wall function)的半经验方法来计算壁面与充分发展湍流区域之间的黏性影响区域。另一种方法则是修改湍流模型使其能够求解近壁的黏性影响区域,称为壁面模型法(wall model)。本文模拟就是使用了壁面模型法。
目前最常使用的壁面模型是M-O壁面模型,该模型基于Monin-Obukhov相似率,假设壁面处的应力张量τs形式为
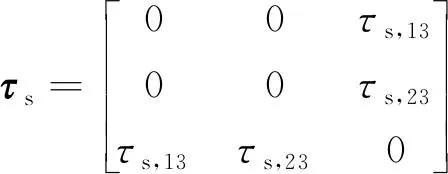
(3)
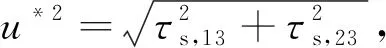
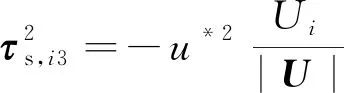
(4)
式(4)中:|U|是下垫面上部第一个节点中心点的速度值,而Ui是其在x和y方向上的速度分量。
2 计算结果及讨论
2.1 模式准确性验证
首先对计算模型的准确性进行验证。模拟一个平坦下垫面情况下大气边界层中风场以及温度场变化的标准算例,并与文献[27]的结果进行比对。该算例的计算设置可参见文献[27]。图2展示了在平坦下垫面情况下,运用OpenFOAM所计算的标准算例中平均风速的垂直分布。该算例中的平均风速和风向在计算9 h后达到稳定状态。从图2可见,风速随高度增加,并且在150 m左右达到超过9 m / s的峰值,随后在高空处降低至初始设置的地转风速(8 m/s)。此外,模拟中地表风的风向达到36°[图2(b)],这些风速与风向的结果都与文献[27]中的模拟结果一致,从而验证了OpenFOAM模式计算平坦下垫面时边界层内风场的准确性。此外,计算中还得到地表的摩擦速度约为0.22 m/s,这也与Poulos等[30]在晴朗天气,近地面静风即稳定边界层条件下进行的CASES-99(cooperative atmosphere-surface exchange study)外场观测中所获得的摩擦速度的合理范围(0.22~0.59 m/s)一致。
此外,模式还模拟了复杂下垫面情况下高层建筑标准模型的风荷载算例,即利用CAARC(commonwealth advisory aeronautical research council)模型[31-32]来验证复杂下垫面时OpenFOAM模拟计算的准确性。CAARC模型是验证数值模拟准确性的标准模型之一,其具体设置可见文献[33],并在2/3建筑物高度的水平面上布置20个标准压力的测点位置,用于测量风压系数。目前已有一整套关于CAARC标准算例的详细的实验测量结果,以验证风洞及数值模拟的准确性。图3体现了CAARC模型标准压力测点处的风压系数文献值[33]与OpenFOAM模拟值的对比情况。结果表明OpenFOAM数值模拟结果与CAARC模型实验结果的误差均在5%之内,由此可以得出,OpenFOAM可以很好地模拟复杂下垫面情况下实际大气的风场的变化情况。
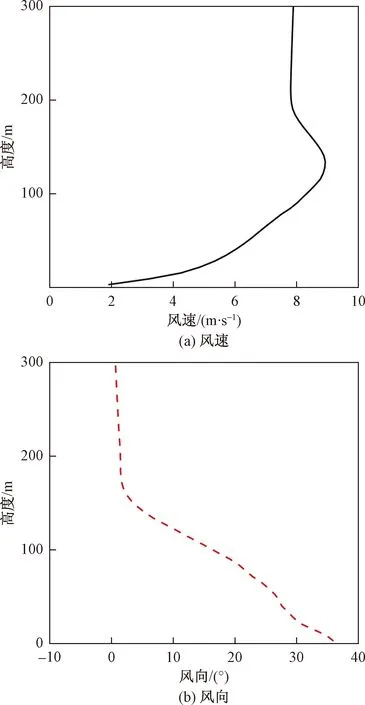
图2 计算9 h后的平均风廓线风速、风向的垂直分布

图3 CAARC模型的风压系数的文献值与模拟值对比[33]
综上所述,OpenFOAM可以很好地捕捉平坦下垫面及复杂下垫面情况下大气风场的变化及分布,因此可以用来进行本文中关于复杂地形条件下风场时空分布的研究。
2.2 模拟结果分析
在研究中进行了固定风向风速(东南西北4个不同风向)共40个算例的模拟,并选取了项目中 46号杆塔处作为中心观测点(x=1 800 m,y=1 800 m),高度为杆塔高度(z=2 336.9 m,相对高度h=35.9 m)。数值模拟计算的空间计算域尺寸为3.6 km×3.6 km×2 km(垂直方向距离下垫面最低点2 km,距离最高点约1.3 km),网格数为100×100×50且中心处加密,中心区域(1.8 km×1.8 km)的空间水平分辨率为30 m,垂直分辨率为40 m。计算时间步为每5 s输出一次计算结果,共输出7 200 s的结果。
以下对不同条件下的计算结果进行展示和分析。
2.2.1 入口为南风3 m/s
图4所示为研究区域的初始入口风向为南风、风速为固定3 m/s情况下,计算7 200 s后的结果。由图4(a)可见,由于在该区域内北部的地形较为平坦,因此计算域北部风处于较为平直的状态。而从图4(b)又可以看到,区域的东南部海拔最高;即地形起伏比较大的地方风速的增大幅度较大。结合图4(a)、图4(b)可以看到,风吹过山脉后,在山峰迎风坡处,由于地形的强迫抬升,使得风速增大,最大值约为4.4 m/s。而同时由于山脉的阻碍作用,在山坡背面风速急剧减小,风速大小降为约1.5 m/s,同时风向也发生了相应的变化。此外,从中还可以发现风吹过山峰后衰减的趋势是相同的,但衰减不同,这可能是由于不同坡度高度的影响所造成的。由侧视图[图4(c)]可以看到,在计算域东北角风向发生了改变,这是由于东北角地形有凸起,地形较周围变化比较剧烈,该处上空处的气流有所增大,并且产生下沉气流。
再截取该计算结果中心点的x方向和y方向的剖面图(图5)。在这些剖面图中,暗色区域代表气块向下运动,亮色区域代表气块向上爬升。从图中x方向的剖面图[图5(a)]中可以看出,在地势变化较为剧烈的区域的近地层内,有大量涡旋湍动混合发生。在此剖面上气流爬升的速度最大可达到 1.0 m/s 左右,约为入口风速的1/3,而下沉气流风速可达到0.4 m/s左右。而从y方向的剖面图[图5(b)]可以看出,在风向垂直于该剖面时,在山峰的两侧,风基本上处于向外流动的状态,即是在斜坡表面的两侧,由于地形的变化,风向会转为下谷风,而且该下谷风往往会出现极强阵风的状态。从中可以看出上升气流最大,约为0.6 m/s,下沉气流风速达到0.7 m/s。
而从不同高度的z方向的剖面图(图6)中可以看出风速流动的趋势。在2 300 m高度处[图6(a)],由于东南部地形存在山峰,只能看见山峰背风坡为小风速,在0~1 m/s。而在高度为 2 400 m[图6(b)]和2 500 m[图6(c)]处,可以看到由于地形的爬升,风速在入口处逐渐增大,而当遇到地形的陡然上升时,由于山坡的阻挡作用,该高度处的风速在山峰的背风坡迅速下降到0~1 m/s。

图4 南风3 m/s时计算结果的俯视图、全景图和侧视图

图5 计算域中心点处x方向和y方向的剖面图
图7所示是取中心探测点(x=1 800 m,y=1 800 m,地面高度35.9 m即46号杆塔高度)处的风速变化情况,可以看出,在南风情况下,x方向上的风速Ux在一段短暂的计算震荡后达到稳定,其值在0.5 m/s左右,而y方向上的风速Uy在稳定后也保持在2.6 m/s的状态,而垂直方向上的风速Uz因为该点位于背风坡为下沉气流,约为-0.15 m/s。

图6 不同高度处的风场剖面图
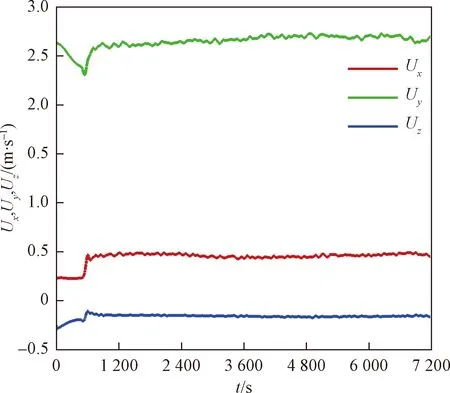
图7 南风3 m/s时探测点风速随时间变化
2.2.2 入口为南风6~30 m/s
当风向为南风时,分别计算入口风速为6~30 m/s 情况下的结果。图8中显示了入口风速为 6~15 m/s时各速度分量随时间的变化,经一段时间后x、y方向分量均达到稳定。表1所示是南风不同入口风速条件下中心探测点风速的x、y、z方向分量的模拟结果。可以看出,该中心探测点处的速度基本随入口风速的增加而增加。相对于入口风速来说,探测点风速在y方向(即南风方向)上的分量有约10%的衰减。而在垂直方向上均为下沉气流。各风速分量情况均与3 m/s入口风速情况一致。图9 所示则是对各分量的拟合结果,图9表明,探测点风速各方向分量的数值变化基本与入口风速的变化一致,并呈线性关系。在x方向上的风速增量变化约为入口的风速增量的15%,在y方向上的风速增量则约为入口风速增量的91%,而在z方向上的风速增量为入口风速增量的6%且呈负相关关系,即计算域南部入口风速的增大会使该探测点处的下沉气流速度增加。

表1 南风条件下各不同风速时中心探测点处风速统计
2.2.3 其他风向固定风速3 m/s
在模拟了南风不同入口风速的基础上,对其他风向入口风速为3 m/s的情况进行了模拟分析。
由图10可得,在北风情况下,各方向风速在计算开始时波动都较大,探测点处x方向上的风速在计算时间内由0左右增大到1.4 m/s左右稳定,而y方向上的风速逐渐减小,并由初始入口风速的南风3 m/s减小为0.9 m/s。垂直方向上的风速由正值转为负值即由上升气流变为下沉气流,最后稳定在-0.3 m/s。
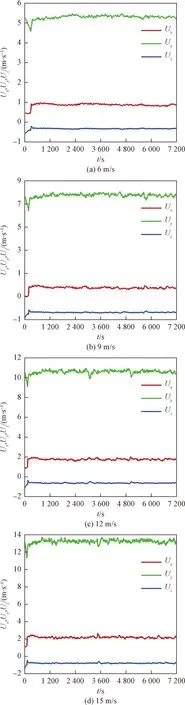
图8 南风不同入口风速时探测点风速随时间变化

图9 南风不同入口风速条件下探测点风速趋势图
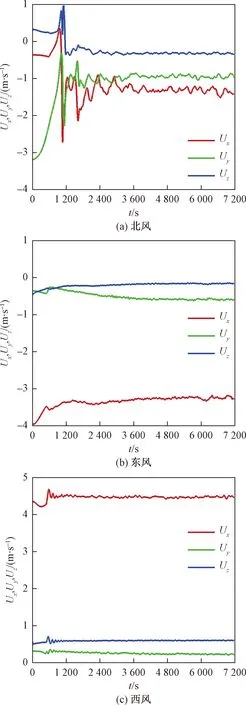
图10 不同风向条件下初始入口风速为3 m/s探测点风速随时间的变化
东风条件下该探测点上x方向上的风速增大,至-3.3 m/s左右保持稳定。y方向上的风速在计算时间内稳定在0.6 m/s。东风情况下该点垂直方向上的风速稳定在-0.2 m/s左右。由此可见在东风情况下,探测点的风速大小受地形变化并不明显。
西风情况下的x方向的风速则比入口风速增大了约50%,这也是4种风向中增大最明显的一个情况。并且在垂直方向上,当吹西风时空气的上升速度最大。因此,选取西风条件下的不同入口风速进行进一步模拟和研究。
2.2.4 入口为西风3~30 m/s
在分析各个方向初始入口风速3 m/s的情况后,发现西风条件下的x方向的风速比入口风速增大了约50%,由此,又对西风6~30 m/s进行了计算,来研究西风对观测点风速变化的影响。表2所示为固定入口风向为西风,风速3~30 m/s的计算结果,图11显示了入口风速与观测点处风速的x、y、z方向上分量的拟合关系。可见在不同的西风入口风速条件下,观测点x方向上的风速均为初始入口风速的1.5倍,且为线性关系,相关系数更是达到了0.99。而风速在y方向上的分量约为入口风速的7%,z方向则全部为上升气流,其值达到入口风速的20%。
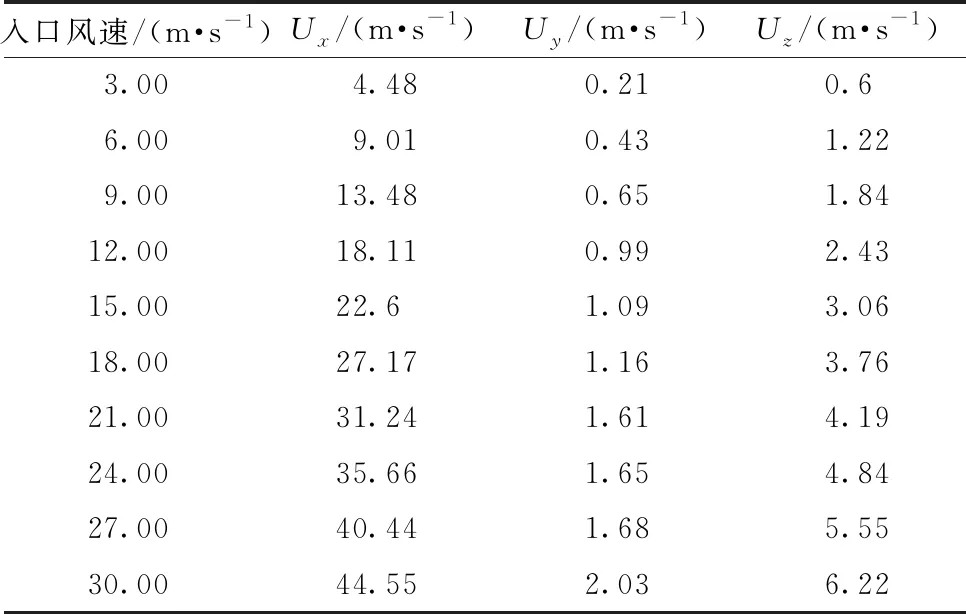
表2 西风条件下各不同风速时中心探测点处风速统计
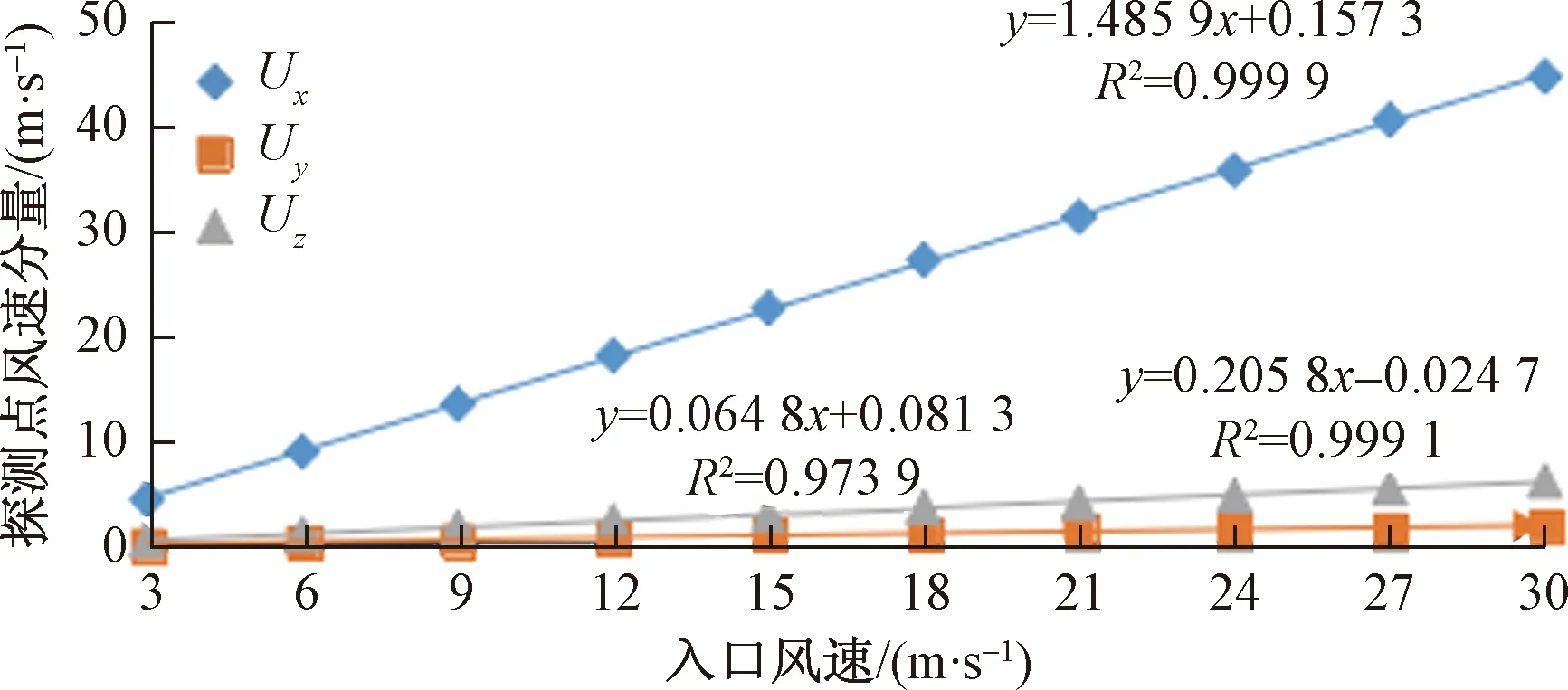
图11 西风不同入口风速条件下7 200 s后探测点风速趋势
进一步探究初始入口风速为西风时,探测点风速增大的原因。由图12所示的研究区域地形图可知,研究区域东南部和中北部分别有高海拔山峰存在,东南部山峰更是高达2 450 m,相对地面高度约为700 m。当风从西边匀速吹来时,即是从广阔的低海拔区域吹向两座山峰中的峡谷区域,因此产生了漏斗效应,致使风在吹过观测点时风速增加。此外,观测点风速增加的另一个原因则是由于观测点地处研究区域东南部山峰的迎风坡,风速在爬坡过程中也会产生增加。

图12 模拟区域二维地形图
2.2.5 大风预报应用
为了加强数值模拟结果在实际大风预报中的应用,统计分析了2016—2019年云南大理地面风场的实测数据,并与数值模拟的研究结果进行比对,以提高研究中所得到的结论在实际风场预报应用中的价值。
图13所示是利用美国国家气候数据中心(U.S.National Climatic Data Center, NCDC)[34]上获取的2016—2019年云南大理地面风场观测数据所绘制的大风(风速大于17 m/s[5])风向的频率玫瑰图。该数据每年更新。从图13中可以看到,在云南大理处,当风向为西风时,2016—2019年每年的大风频率都在20%以上,且远高于其他风向,而这也与研究中模拟所得到的结论一致。由此,通过该实测数据以及研究中的数值模拟结论可得到,未来在大理的大风预报中,可重点关注西风条件下风速的变化,并做好相应防风措施,从而在最大程度上减少大风灾害所带来的影响。
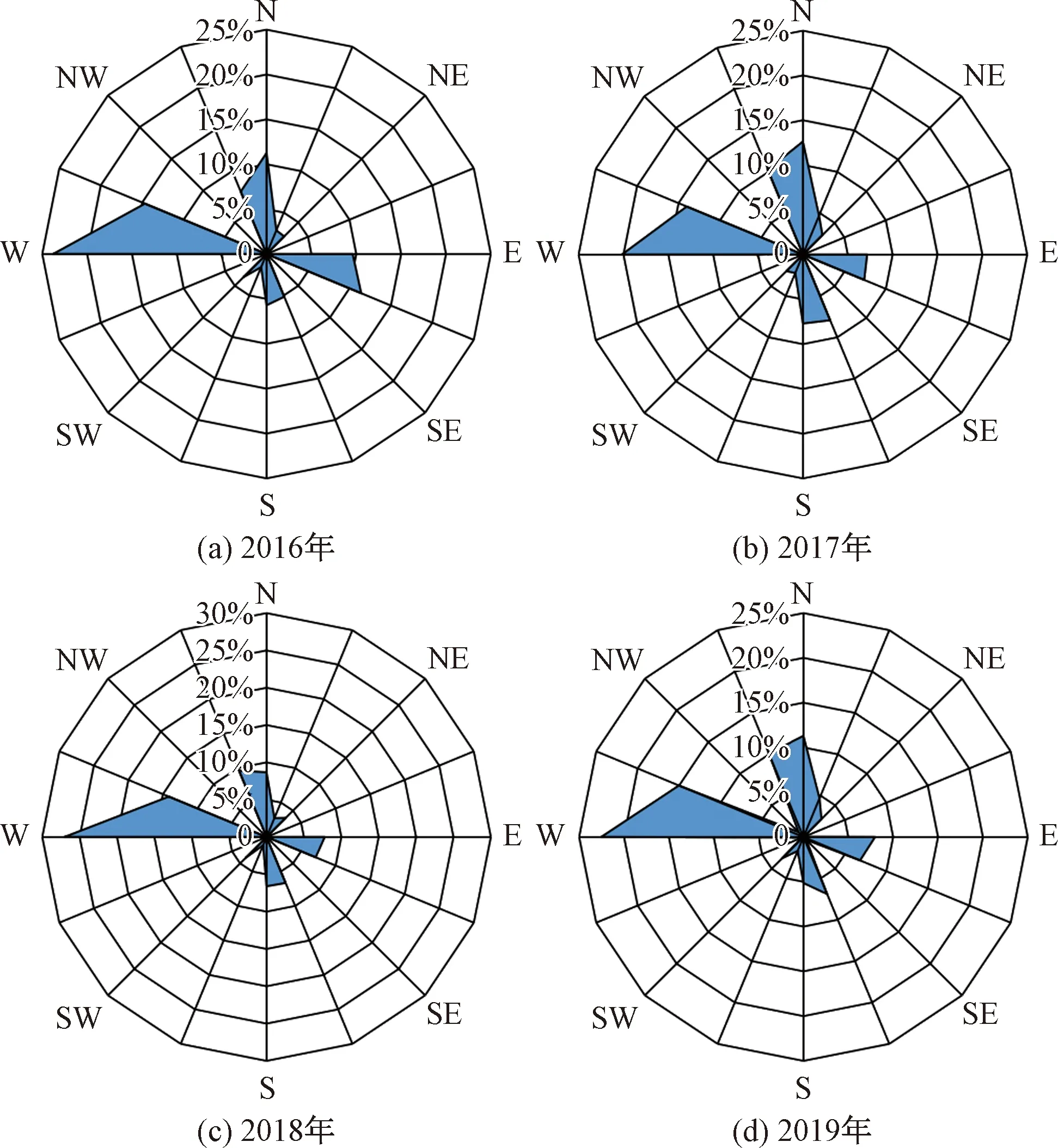
图13 2016—2019年云南大理大风日数各风向频率玫瑰图
3 结论
(1)根据计算结果,云南大理白族自治州南部(100.24°N,24.83°E)微环境地形下山峰迎风坡处,由于地形的强迫抬升会使局部风速增大,而当同时由于山脉的阻碍作用,在山坡背面坡风速则会急剧减小,同时风向也会发生变化,产生尺度较小的涡旋以及不规则的回流。
(2)由不同风向固定风速的计算,发现该区域中心点在吹西风时由于漏斗效应水平风速有明显增大情况,x方向上分量约为入口风速的1.5倍,而入口风速为其他风向情况下水平风速则没有太大的变化。而在垂直方向上,在吹西风的情况下,该探测点处会产生明显的上升气流,而其他风向情况下均为下沉气流且都接近于零。
