区间直觉模糊群决策方法及其在高校人才引进中的应用
2020-12-14马正瑞张媛媛
马正瑞,李 明,张媛媛
(1.中国矿业大学银川学院 人文学院, 宁夏 银川 750021; 2.北方民族大学 商学院, 宁夏 银川 750021)
人才是社会进步和发展的重要资源,是强国的坚强后盾。在社会的整个发展过程中存在着许多竞争,但核心竞争归根结底还是人才竞争,而高等院校是培养高级人才的主要摇篮。随着社会经济的飞速发展,我国各个高等院校开始意识到高层次人才的引进对提高教学质量、提升教师队伍素质及提高高校综合竞争力的重要性。
高等院校人才引进本质是一系列复杂的决策过程,该过程涉及到高校的师资能力、科研实力和战略发展,需要校方管理者和学科专家共同参与。对于复杂的高校人才引进决策问题,多属性群决策以其特有的优势——集结各个领域专家的智慧来获得更科学的决策结果而越来越引起研究人员的重视[1]。针对多属性群决策问题,文献[2]根据构建的八个属性指标,基于广义有序加权混合对数平均算子提出了高校引进人才的多属性决策方法,以此确定高校人才的最优选拔;许玲[3]提出了基于H-平均的广义直觉信息集成算子,研究了高校向国内外招聘人才的最优决策模型;Yu等[4]在区间值直觉模糊信息背景下,构建了高校引进人才的多属性群决策模型,并对应聘人才进行了最优排序。
上述研究结果表明,面对高等院校引进人才的决策问题,多属性群决策方法已经得到了很好的应用。然而,文献[2]中决策者用实数描述对候选人才的评价,这会造成决策信息的不完整或信息损失,不能完整地表述决策者的评价意见;尽管文献[3]利用直觉模糊信息来描述对候选人才的评价,但在现实生活中,由于决策信息的不充分、不确定,直觉模糊信息的隶属度和非隶属度用精确值来描述有失信息的完整性;文献[4]决策者通过区间直觉模糊数对候选人才进行了评价,其隶属度和非隶属度都是以区间数形式给出,使区间直觉模糊数具有了双重不确定性,从而降低了数据的处理效率,增加了群决策的难度;该文献中的区间直觉模糊优先平均算子是基于区间直觉模糊集的代数运算法则提出的,这虽然能克服用二元运算进行集结过程最终结果的精度不足,但与一般模糊集的极限情况却不一致。另外,在信息集结过程中,只考虑了隶属度和非隶属度区间左右两个端点的信息,而忽略了区间上其它点的信息,对决策结果有一定的影响。因此,有必要介绍新的群决策方法用于解决高校人才引进的决策问题,以此来提高群决策的准确性和科学性。
在多属性群决策问题中,集结各决策者的评价信息是解决此类决策问题的关键所在[5]。为了提高区间型直觉模糊数的处理效率,降低群决策难度,保证决策信息的完整性,并在信息集结过程中,既能充分考虑区间上每个点的信息,又能在克服用二元运算得到最终结果精度不足的基础上,与一般模糊集运算的极限情况保持相一致。本文在文献[4]的研究背景的基础上,提出了连续区间直觉模糊Einstein加权几何平均(C-IIFEWGA)算子, 连续区间直觉模糊Einstein有序加权几何平均(C-IIFEOWGA)和连续区间直觉模糊Einstein混合几何平均(C-IIFEHGA)算子,并且讨论了这些算子的性质。最后, 基于C-IIFEHGA算子提出了一种解决高校引进人才的多属性群决策方法。通过对比分析,该方法主要优点是将Einstein运算和C-OWA算子结合,不仅考虑了区间直觉模糊集运算的极限情形,而且全面考虑了隶属度和非隶属度区间上所有的信息点,降低了数据处理的复杂性,提高群决策的合理性和科学性。
1 预备知识
为了便于本文的研究,本小节简单介绍了直觉模糊集、区间直觉模糊集的相关概念和运算法则,以及直觉模糊数的Einstein运算法则和C-OWA信息集结算子。
1.1 直觉模糊集和区间直觉模糊集
定义1[6]设X是一个非空集合,A={〈x,μA(x),vA(x)〉:x∈X}为X上的一个直觉模糊集,其中,函数μA:X→[0,1],vA:X→[0,1]且满足0≤μA(x)+vA(x)≤1,μA(x)表示元素x属于直觉模糊集A的隶属度,vA(x)表示元素x属于直觉模糊集A的非隶属度。数对(μA(x),vA(x))称为一个直觉模糊数,对于每一个直觉模糊数可简单地定义为α=(μα,vα),且满足μα∈[0,1],vα∈[0,1],0≤μα+vα≤1。此外:
S(α)=μα-vα
(1)
称为直觉模糊数α的得分函数[7],而:
H(α)=μα+vα
(2)
称为直觉模糊数α的精确函数[8]。
为了能比较任意两个直觉模糊数α=(μα,vα)和β=(μβ,vβ)的大小,Xu和Yager[9]根据直觉模糊数的得分函数和精确函数提出了如下的比较方法,我们以定理的形式给出。
定理1[9]设α和β是两个直觉模糊数,
1) 如果S(α) 2) 如果S(α)=S(β),则有 i) 如果H(α)=H(β),则有α=β。 ii) 如果H(α) 然而,在现实生活中,由于客观事物的复杂性和模糊性,μα和vα的值往往无法用实数表示,而用区间数表示比较适合,因此,Atanassov和Gargov[10]对直觉模糊集进行了拓展,得到区间直觉模糊集,其定义见下。 [bL,bU]),且满足[aL,aU]⊆[0,1],[bL,bU]⊆[0,1],aU+bU≤1。 为了便于定义,在本文中,用M表示所有直觉模糊数所组成的集合,Ω表示所有区间直觉模糊数所组成的集合。 设α=(μα,vα)和β=(μβ,vβ)为任意两个直觉模糊数,k>0为任意实数, 则直觉模糊数的Einstein乘积运算,Einstein求和运算、Einstein数乘运算以及Einstein幂运算[11-12]可定义如下: (3) Yager于2004年提出连续区间有序加权平均(C-OWA)算子[13],该算子借助于态度参数将区间数表示成实数形式,且态度参数直接反映了决策者的风险态度,其定义如下。 (4) 则称F是连续区间的OWA算子,简称为C-OWA算子,Q(y)为基本的BUM函数。 为了简化式(4),C-OWA算子满足如下定理。 FQ([xL,xU])=γxU+(1-γ)xL (5) 基于直觉模糊数的Einstein运算和C-OWA算子,本小节将提出加权几何平均算子用于集结区间直觉模糊偏好信息。 (6) 根据直觉模糊数的Einstein运算法则,C-IIFEWGA算子可以转换为如下的n维函数的形式。 (7) 证明:首先,利用数学归纳法证明式(7)成立。设 i=1,2,…,k+1,当n=2时,利用直觉模糊数Einstein运算法则和式(4)计算得: (8) 结论成立。 假设n=k时,结论也成立,即: (9) 当n=k+1时,则: (10) 结论成立。因此,根据以上证明,对于任意的n,式(7)都成立。 其次,证明集结结果仍为一个直觉模糊数。 由于 则根据式(4),可得: (11) 从而: (12) (13) 因此: (14) (15) 且: (16) 综上可得: (17) 仍为一个直觉模糊数。 证毕。 C-IIFEWGA算子满足幂等性、有界性和单调性,这些性质具体描述见下。 (18) (19) 证毕。 (20) 证明:设T为C-IIFEWGA算子,且 i=1,2,…,n,首先证明 由于: (21) (22) (23) 则: (24) 且: (25) 利用式(1)计算得: (26) 即: (27) 同理可证: (28) 证毕。 成立, 则: (29) 证明:设T为C-IIFEWGA算子, i=1,2,…,n且f(t)=(2-t)/t,t∈(0,1]。 因为f(t)=(2-t)/t是一个关于t的单调递减函数,且FQ(ai)≤FQ(ci),则: (30) 设g(t)=(1-t)/(1+t),t∈[0,1]。因为g(t)是一个关于t的单调递减函数,且FQ(bi)≥FQ(di),则: (31) 于是: (32) 进一步得: (33) 于是就有: (34) 最后整理得: (35) 根据式(1)计算得: (36) 因此: (37) 证毕。 (38) 称为连续区间直觉模糊Einstein有序加权几何平均算子,简称为C-IIFEOWGA算子。其中W=(w1,w2,…,wn)T是相关的权重向量,且满足 同理,根据直觉模糊数的Einstein运算法则,C-IIFEOWGA算子可以转换为如下的n维函数的形式。 (39) 式中:W=(w1,w2,…,wn)T是相关的权重向量,且满足 C-IIFEOWGA算子满足幂等性、有界性、单调性和置换不变性,其中幂等性、有界性和单调性与C-IIFEWGA算子的性质类似,在此不再赘述, 而置换不变性可描述如下。 (40) 证明:设T为C-IIFEOWGA算子,则: (41) 和: (42) (43) 成立。 证毕。 由定义4可知,C-IIFEWGA算子主要研究的焦点是强调集结参数本身的重要性,而定义5指出C-IIFEOWG算子主要研究的焦点是强调了集结参数所处位置的重要性。也就是说,C-IIFEWGA算子和C-IIFEOWGA算子都仅仅只反映了其中的一个方面,具有一定的片面性。因此,基于C-IIFEWGA算子和C-IIFEOWGA算子,提出连续区间直觉模糊Einstein混合几何平均(C-IIFEHGA)算子,其定义为如下。 (44) 为相关的权重向量,且满足 类似于定理3,根据直觉模糊数的Einstein运算法则,C-IIFEHGA算子可以转换为如下的n维函数形式。 (45) 为相关的权重向量,且满足 特别地,当ω=(1/n,1/n,…,1/n)T时,则C-IIFEHGA算子退化为C-IIFEWGA算子;当W=(1/n,1/n,…,1/n)T时,则C-IIFEHGA算子退化为C-IIFEOWGA算子。 C-IIFEHGA算子也具有幂等性、有界性、单调性和置换不变性,这与C-IIFEOWGA算子类似,其证明过程可参阅性质1~4。 i=1,2,…,m,j=1,2,…,n,k=1,2,…,l。 下面基于C-IIFEHGA算子提出一种解决上述群决策问题的方法,具体步骤为如下。 (46) (47) 在本小节里,利用本文第3部分所提的方法来解决高校引进人才的群决策问题[4]。某高校打算从海外引进杰出人才,组织了一个由3人组成的专家组,分别为学校校长d1,管理学院院长d2和人事处处长d3,他们将从c1-思想道德、c2-科研能力、c3-教学技能和c4-教育背景4个方面对5位候选者xi,i=1,2,3,4,5提供的信息资料进行严格的审核,并根据候选人才提供的信息资料给出相应的评价值,具体评价信息值见表1~3。 表1 决策者d1提供的决策矩阵 表2 决策者d2提供的决策矩阵 表3 决策者d3提供的决策矩阵 为了便于计算,我们假设BUM函数为Q(y)=y2,属性权重向量为W=(0.3,0.2,0.4,0.1)T,专家权重向量为V=(0.35,0.35,0.3)T。基于以上信息,利用所提的决策方法对5位候选者进行排序,具体决策过程见下列步骤。 (48) 计算结果见表4。 表4 综合决策矩阵Tab.4 Collective decision (49) 得到方案xi的群体综合评价值: (50) (51) x2≻x5≻x1≻x4≻x3 (52) 因此,最优的候选人才是x2,在此人力资源群决策问题中,最优人选是第二个候选者,这与文献[4]的最终决策结果一致,说明本文提的方法是有效的、合理的。但是,两种方法得到的五个候选人才最终排序却不一致。在文献[4]中,五位候选人才的最终排序为: x2≻x4≻x5≻x1≻x3 (53) 为了进一步说明排序上的差异性,以及所提方法的优越性,现根据已知的客观数据,对本文所提的多属性群决策方法与文献[4]所提的决策方法进行对比分析。 利用文献[4]所给的得分函数公式: S=(2+aL+aU-bL-bU)/4 (54) 分别计算表1~3中候选人才x1,x4和x5评价值的总得分值,结果见表5。 表5 候选人得分对比Tab.5 Comparison of candidates’ scores 由表5可得,在属性权重和决策者权重一致的情况下,利用式(54)计算候选人才x5客观评价信息的总得分值为7.60,为三个候选人才中最大的;其次是候选人才x1的,总得分值为7.575,最后是候选人才x4的,总得分值为7.25。根据定理1,可得: x5≻x1≻x4 (55) 这与本文所提决策方法得到的最终决策结果是完全一致的。事实上,一方面,根据信息集结算子满足的幂等性可知,利用信息集结算子对偏好信息进行多次集结后并不能改变备选方案本质上的优先顺序[15]。而本文提出的方法在评价信息的集结过程中,C-IIFEHGA算子既满足了幂等性,又充分考虑了模糊集运算的极限形式,尽可能地将候选人才的客观评价信息的损失降到最低;另一方面,C-IIFEHGA算子既考虑了每个评价信息所处位置的重要性,又考虑了每个评价信息自身的重要性,且在信息集结过程中,信息集结算子采用的是有序加权平均,而非简单的加权平均,可去除一些主观因素,有效防止带有主观因素的决策者给出错误的评价[15]。因此,本文提出的决策方法得到的决策结果更客观,更合理。 另外,为了分析不同态度参数对信息集结结果影响。现分别选取不同的态度参数γ的值,即0,0.1,0.2,…,0.8,0.9,1,这些态度参数值都是由决策者所提供,利用本文所提的方法,可得各个候选人才综合评价值的得分函数S与态度参数γ的关系,见图1。 图1 S与γ的关系图Fig.1 Relationship between S and γ 此外,图1还显示如下结论。 1)当0≤γ≤0.7时,五位候选人才的排序结果为x2≻x5≻x1≻x4≻x3,其中最优候选人为x2。 2)当0.7<γ≤1时,五位候选人才的排序结果为x5≻x2≻x1≻x4≻x3,其中最优候选人为x5。 由此可知,随着态度参数γ的取值不同,候选人才的排序也随着变化,从而导致产生不同的决策结果。因此,在高校人才引进的群决策问题中,决策者可以根据实际需求和自身的决策心理态度,选择参数γ的值来进行科学有效的决策。 在这个全新的时代,人才对于高等院校的长远发展具有不可估量的作用,各个高校非常重视人才引进工作。为了能科学、合理地解决高校引进人才的决策问题,本文提出了几个连续区间直觉模糊Einstein加权几何集结算子,包括C-IIFEWGA算子、C-IIFEOWGA算子和C-IIFEHGA算子。在相关权重取特殊值时,C-IIFEHGA算子可分别退化为C-IIFEWGA算子和C-IIFEOWGA算子,并研究了它们的一些相关性质。此外,基于C-IIFEHGA算子,提出了一种解决高校引进人才群决策问题的方法,对候选人才进行了最优排序。该方法能够将区间直觉模糊数通过态度参数转化为直觉模糊数,充分利用了隶属度和非隶属度区间上所有的信息点,降低了参变量的不确定性和数据处理的复杂性,考虑了集结参数位置的重要性和集结参数自身的重要性,并在克服用二元运算集结所得最终结果精度不足的基础上,与一般模糊集运算的极限情况保持相一致,从而提高了群决策的准确性。此外,通过分析态度参数γ在信息集结过程中所发挥的作用,决策者可以根据自己的喜好和实际的需要来选取态度参数值进行群决策,以此保证决策结果的合理性和科学性。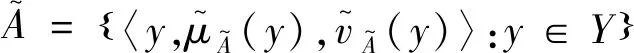
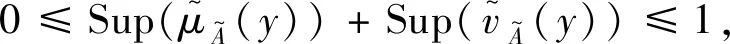
1.2 直觉模糊数的Einstein运算
1.3 C-OWA算子
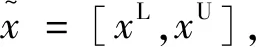


2 连续区间直觉模糊Einstein加权几何集结算子






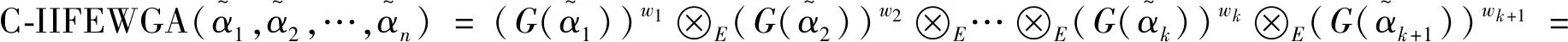




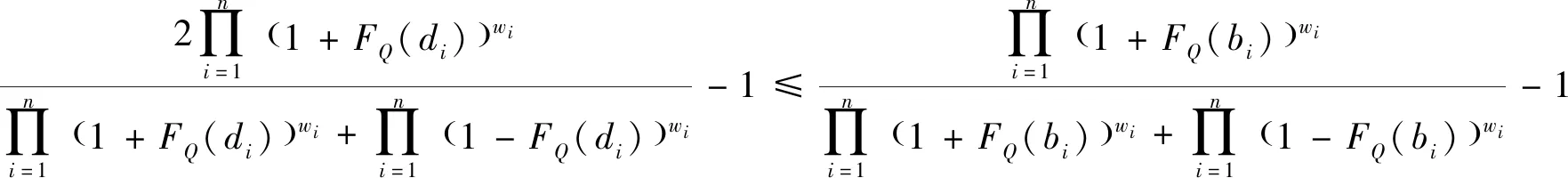
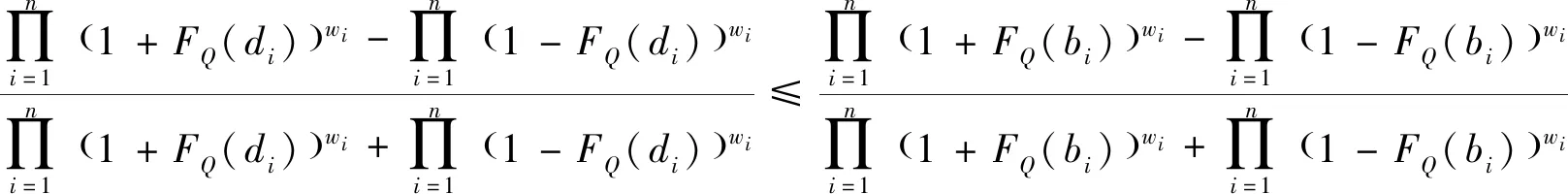





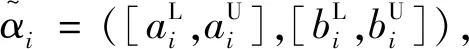
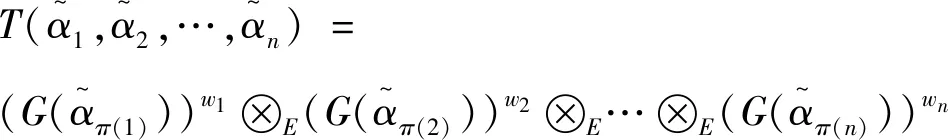
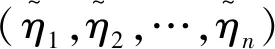




3 基于C-IIFEHGA算子的群决策方法

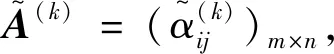


4 算例分析



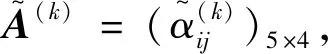
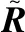


5 结 论
