快速评价海水入侵区地层渗透性实验研究
2020-12-13戴云峰林锦郭巧娜孙晓敏陈永强刘九夫
戴云峰林 锦郭巧娜孙晓敏陈永强刘九夫
(1. 南京水利科学研究院 水文水资源与水利工程科学国家重点实验室,江苏 南京 210029;2. 南京水利科学研究院 地下水研究中心,江苏 南京 210029;3. 河海大学 地球科学与工程学院,江苏 南京 211100)
1 研究背景
国外学者对振荡试验开展了非常丰富且深入的研究。Hvorslev[1]首次通过观测水位恢复过程现场确定土体的渗透系数,并且推导了不同含水层和测试井结构条件下渗透系数计算公式。Cooper等[2]和Papadopulos等[3]推导了振荡试验确定承压含水层渗透系数的半解析解,绘制了一系列过阻尼振荡试验测试井中水位恢复标准曲线(以下统称“Cooper模型”)。Kamp[4]分析了考虑惯性效应的振荡试验测试井中水位恢复过程,Kipp[5]基于Cooper模型和Kamp模型推导了从过阻尼振荡到欠阻尼振荡试验情形下确定含水层渗透系数的半解析解。Bouwer和Rice[6]基于稳定态井流Thiem公式提出了确定非承压含水层渗透系数的振荡试验模型,并且推导了试验影响半径与测试井、含水层几何尺寸关系的经验公式(以下统称“Bouwer&Rice模型”)。Hyder等[7-8]提出了可分析承压含水层和非承压含水层非完整井中振荡试验半解析解模型(以下统称“KGS模型”)。Butler等[9-12]基于阻尼弹性解理论推导了高渗透性含水层非完整井振荡试验半解析解(以下统称“Butler模型”)。Malama等[13]改进了非承压含水层中考虑观测井振荡过程的跨孔振荡试验半解析解模型,并验证了该模型在分析多井和多层含水层气压式振荡试验中的可行性。
国内学者对振荡试验的研究起步较晚。在相当长一段时间内振荡试验在国内并没有获得广泛的应用,主要原因是:没有针对振荡试验的应用规范;没有专门实施振荡试验水位差激发和水头响应采集的仪器。周志芳等[14-15]研究了裂隙介质中的振荡试验,参与编制了国内首本振荡试验企业标准《钻孔振荡式渗透试验规程》(Q/CHECC 005-2009)以及能源行业标准《水电工程钻孔振荡式渗透试验规程》(NB/T 35117-2018),开发了高精度振荡试验测试系统。戴云峰等[16-18]基于Kipp模型推导了考虑含水层倾角影响的振荡试验半解析解,并确定了倾角影响的临界角度;基于Cooper模型和Kipp模型推导了考虑含水层径向定水头边界影响的振荡试验半解析解。Liu等[19]提出了裂隙区域中新的双重介质振荡试验模型,结果表明裂隙倾角越大振荡越剧烈,当裂隙倾角大于30°时必须要考虑倾角对振荡试验的影响。Wang等[20]提出了适用于承压含水层存在越流补给的振荡试验模型,模型将承压含水层中的水平流作为非达西水平流而弱透水层中为达西流和垂直流。Liang等[21]在非饱和-饱和含水层系统中分析了井壁效应和振荡响应对欠阻尼振荡试验的影响。
为给海水入侵区水文地质模型、水流及溶质运移数值模拟模型等提供高精度渗透系数,提高现场确定海水入侵区含水层渗透系数的效率,减少水文地质试验对存在污染含水层的扰动。本文首先在利用山东龙口海水入侵区含水介质构建的砂槽物理模型中进行注水式振荡试验,在人工潜水含水层和承压含水层中同步监测试验主井和相邻观测井中水位响应,通过室内实验确定多层仿真含水层系统渗透系数;结合室内实验的经验和渗透系数值,进一步在龙口海水入侵区地下水分层监测井中实施提水式和注水式振荡试验,快速评价不同埋深地层渗透性。
2 砂槽物理模型实验
振荡试验,相对于抽水试验和压水试验是一种非常规水文地质试验手段,通过短时间在测试井中激发水头变化(升高或降低),记录测试主井和观测井中水位恢复到初始状态的响应过程,基于半解析解模型分析水位(水头)响应过程以计算目标地层的水文地质参数。
长期以来,国内外学者关于振荡试验的研究成果主要集中在振荡试验理论模型的推导,主要考虑因素有目标含水层类型(承压含水层、非承压含水层)、测试主井类型(完整井、非完整井)、是否利用观测井进行实验、是否考虑测试井—含水层系统的惯性效应(欠阻尼振荡、临界阻尼振荡、过阻尼振荡),统计结果见表1。苏锐等[22]对振荡试验主要理论模型的适用条件和优缺点进行了总结。

表1 振荡试验半解析解模型适用条件

图1 海水入侵砂槽物理模型
2.1 海水入侵含水层室内仿真模型构建结合山东龙口海水入侵区滨海含水层系统的非均质性,Guo等[23]在河海大学地球科学与工程实验中心建造了大型滨海含水层海水入侵砂槽物理模型。砂槽物理模型示意图和实物图见图1(a)(b),其长度为6.6 m、高1.5 m、宽0.6 m。砂槽内利用高透水过滤板隔离成3部分,过滤板分别距两侧30 cm,两侧水槽注水模拟海水和内陆边界。砂槽中间填充人工含水层,上部为细砂(厚度0.4 m)、中部为黏土(厚度0.25 m)、下部为含砾粗砂(厚度0.5 m),模型使用的细砂、黏土和粗砂均从山东省龙口市海水入侵区采集,采样剖面见图1(c)。砂槽模型多层含水层系统中布设有两组潜水井和承压井,潜水井底位于细砂和黏土的接触面;承压井底位于粗砂底部,外径均为80 mm,内径约75 mm,外布设在距右侧内陆边界2.0 m和1.0 m位置。
2.2 实施室内振荡试验大型滨海含水层砂槽模型中潜水井和承压井均为完整井。为确定介质为含砾粗砂承压含水层水文地质参数,在3#测试井中共进行3组注水式振荡试验,注水量分别为1.0 L、2.0 L和3.0 L,1#井作为观测井同步记录含水层水头响应。为确定介质为细砂潜水含水层水文地质参数,在4#测试井中共进行3组注水式振荡试验,注水量分别为0.5 L、1.0 L和1.5 L,2#井作为观测井同步记录含水层水头响应。室内实验过程中测试井内压力传感器采集频率为1(即1秒钟采集1个数据)。砂槽模型中6组实验测试井中水位相对初始水位变化过程和观测井中相对初始水位变化过程见图2(图中w为测试井中水位变化值,w′为观测井中水位变化值),室内实验过程中受两侧定水头水位控制装置性能影响,砂槽含水层中水位整体存在波动干扰。

图2 注水式振荡试验过程中测试井和观测井中水位变化
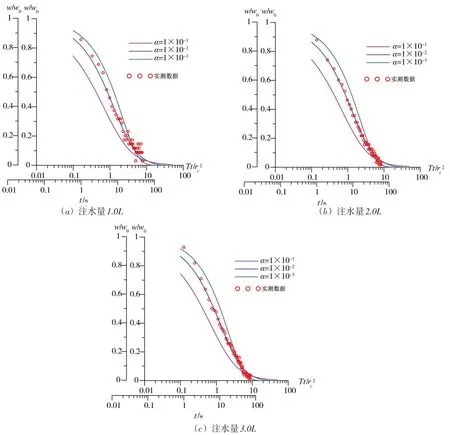
图3 3#测试井中无量纲水位变化配线结果
当在承压含水层中进行振荡试验时,观测井中水位对测试主井中水位变化响应非常迅速;测试主井不同注水量条件下水位初始上升高度约12.6 cm、23.3 cm和29.4 cm,此时观测井中水位上升幅值分别约为2.2 cm、4.3 cm和5.0 cm。当在潜水含水层中进行振荡试验时,测试主井不同注水量条件下水位初始上升高度约7.9 cm、15.8 cm和24.7 cm,未监测到观测井中水位对测试主井中水位变化有明显响应,主要原因是潜水测试井中注水体积较小、观测井中水位受到的干扰较大。
综上所述,中国的独特文化翻译不能绕道而行,要保留下它的精髓。中国文化虽有异于西方文化,但只要多了解对方的文化背景,也就能够使交流变得自如。
2.3 仿真含水层渗透特性分析当3#作为测试井1#作为观测井时,基于Dai和Zhou推导的模型[17],测试井和观测井中无量纲实测水位变化与标准曲线匹配结果见图3和图4(图中α为无量纲贮水系数,w0为测试井或观测井中水位变化初始值(最大值),t为时间,T为含水层导水系数,rc为测试井套管半径),含砾粗砂承压含水层渗透系数计算结果见表2(表中贮水系数为测试井花管半径;渗透系数K=T/M,T为含水层导水系数,M为目标含水层厚度)。

图4 1#观测井中无量纲水位变化配线结果

表2 振荡试验确定砂槽物理模型中承压含水层水文地质参数

图5 4#测试井中水位变化拟合结果

表3 振荡试验确定砂槽物理模型中潜水含水层渗透系数
当4#作为测试井时,测试井中无量纲水位变化与标准曲线匹配结果见图5,基于Bouwer&Rice模型[6],细砂潜水含水层渗透系数计算结果见表3。潜水含水层渗透系数明显小于承压含水层渗透系数,符合对应含水层介质的渗透特性,由于同期观测井中并未明显监测到水位变化,故仅通过测试主井实验数据计算潜水含水层渗透系数。
室内实验结果显示,砂槽模型中含砾粗砂(山东龙口海水入侵区采集)构成的人工承压含水层渗透系数为40.5 m/d(最小注水量分析结果),细砂构成的人工潜水含水层渗透系数为18.88 m/d(最小注水量分析结果)。无论在承压含水层中或潜水含水层中实施振荡试验,随着注入含水层测试井中水量增加,实验计算的含水层渗透系数值逐渐减小,主要原因是砂槽物理模型宽度只有0.6 m(监测井距离两侧隔水边界仅0.3 m),随着注水量的增加实验过程中振荡传播的半径到达砂槽物理模型侧向边界时,隔水边界的存在导致计算结果误差增加。
大型海水入侵砂槽物理模型主要功能是用于模拟潮汐和海平面上升对海水入侵的影响机理,实施海水入侵砂槽模拟实验之前需要对潜水含水层和承压含水层渗透系数进行测定,抽水试验受模型尺度限制实施比较困难,本文通过实施注水式振荡试验快速确定了仿真潜水含水层和承压含水层渗透系数。现场实验所在龙口市西海岸地下水分层监测剖面的地质勘察结果显示,含水层介质主要为中砂、粗砂和砾砂,室内实验结果为现场实验提供了重要的判断依据,表明龙口市西海岸含水层属于高渗透性含水层,若地下水分层监测井连通良好,实施振荡试验的耗时将较短。
3 龙口海水入侵区现场实验
为了给科学管理沿海地区地下水资源,防治海水入侵等工作提供基础数据,本文选择山东省龙口市作为渤海沿海典型海水入侵区,针对滨海多层含水层系统进行了一系列振荡试验现场实验研究。戴云峰等[24]在广州海(咸)水入侵区无地下水分层监测井地区利用Geoprobe系统在不同埋深地层中实施气压式振荡试验,获取了弱透水层和承压含水层渗透系数。本文利用龙口市西海岸建设的地下水分层监测井,实施振荡试验确定不同埋深含水层渗透系数。
3.1 现场实施振荡试验山东省龙口市的海水入侵始发于1976年,1980年代以来,由于对地下水的不合理开采,如农业灌溉、生活生产用水和煤矿疏干排水等高强度开采,导致滨海含水层地下水出现了采补失衡,地下水水位持续下降,地下水水位负值区逐年增加,进而导致海水入侵面积逐年扩大。龙口市于1990年代开始采取防治措施,海水入侵速度迅速减缓,入侵面积得到有效控制。近年来受连续干旱影响,地表水的缺乏导致地下水开发利用的需求进一步增加,海水入侵防治的压力也逐渐加大。
本文利用龙口市西海岸新建的地下水分层监测井位置见图6,地层剖面见图7。监测剖面由距海岸线不同位置4组地下水分层监测点组成,每组均分3层对地下水水位和水质进行监测,龙口中学位置受场地限制使用一孔多层(DS4),其他3组使用异孔多层监测技术。异孔多层井壁管管材采用180 mm×8.6 mm PVC-U管,一孔多层井壁管管材采用110 mm×5.3 mm PVC-U管。20组振荡试验关键参数见表4。

图6 龙口海水入侵区振荡试验点位分布
相比于抽水试验,振荡试验实施过程耗时非常短,不需要大型抽水设备或钻机设备配合实施,也不需要持续24~48 h抽水以等待测试井中水位稳定。首先在地下水监测井中实施提水式振荡试验,提水式振荡试验恢复后,在保证提水桶清洁的前提下将原水再次注入地下水监测井中,最大程度地减少对监测井周围地下水水位和水质的扰动;无法进行提水式振荡试验的监测井中使用注入少量纯净水的方法实施注水式振荡试验。表4显示除了DS4-2因滤水管(花管)堵塞水位变化没有恢复到初始位置,其他地下水监测井中水位恢复的时长均在5 min之内。

图7 现场实验地层剖面
3.2 不同埋深地层渗透性评价振荡试验理论模型根据井-含水层结构等因素进行选择,现场实验的12眼地下水监测井设计为承压含水层非完整井,测试主井中水位恢复曲线类型变化从欠阻尼振荡到过阻尼振荡。利用不同振荡试验模型绘制的配线图见图8—11(图中wd为Butler模型测试井中无量纲水头变化,td为Butler模型无量纲时间,CD为Butler模型无量纲阻尼参数;τ为KGS模型无量纲时间,H为KGS模型测试井中水位,H0为KGS模型测试井中水位初始振荡高度),含水层渗透系数计算结果见表5(表5第一列试验编号后缀“T”表示在监测井实施提水式振荡试验,试验编号后缀“Z”表示在监测井实施注水式振荡试验)。提水式和注水式振荡试验的实测无量纲水位恢复曲线主要与Butler模型和KGS模型标准曲线匹配较好,部分浅层井中实测曲线与Bouwer&Rice模型和Cooper模型标准曲线匹配较好。注水式振荡试验获取的渗透系数值与提水式振荡试验获得的渗透系数值接近,部分点位振荡试验确定的渗透系数值小于抽水试验确定的渗透系数值。室内砂槽物理模型中确定的含砾粗砂含水层渗透系数与现场实验确定的含水层渗透系数值接近。
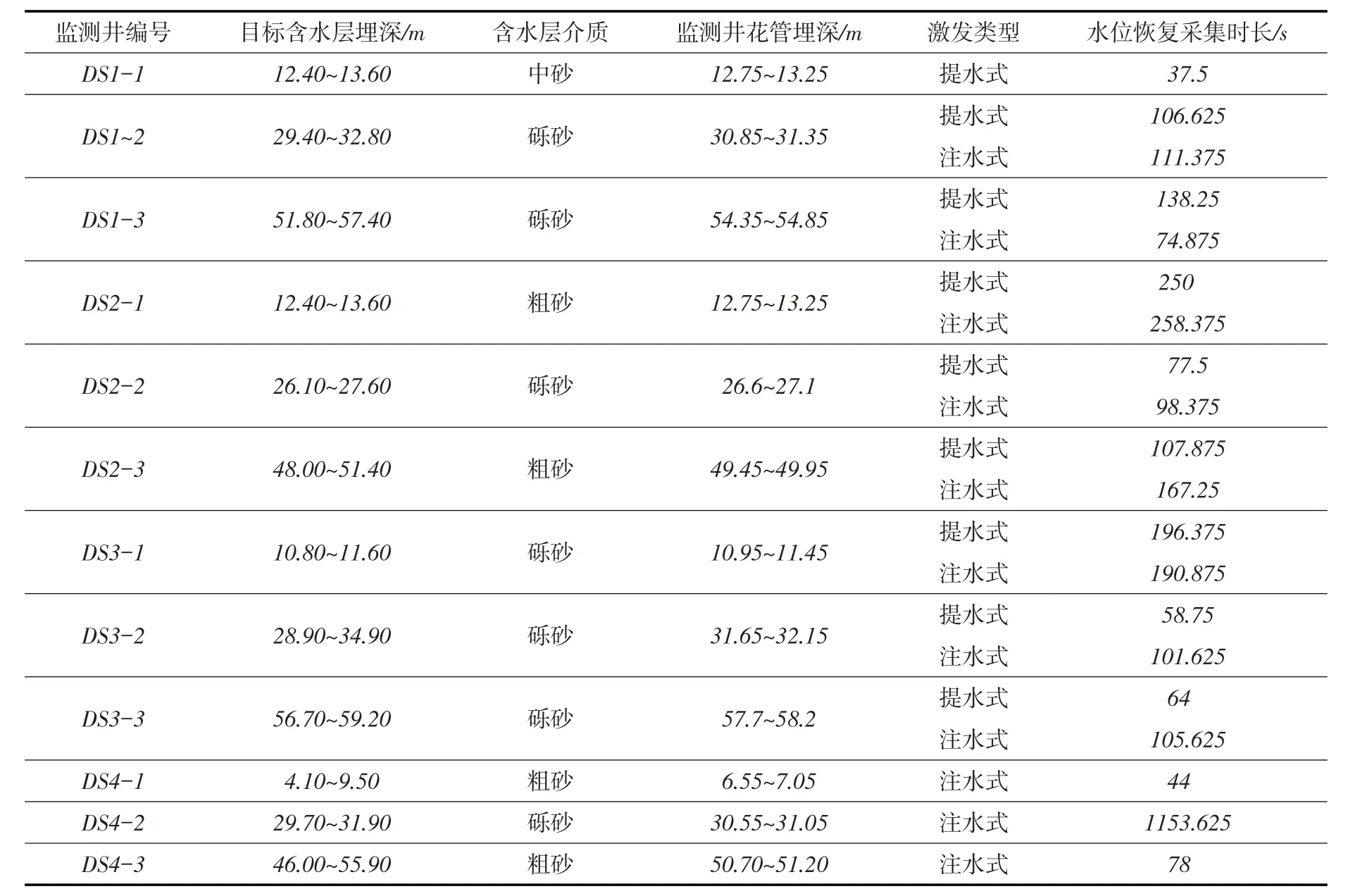
表4 振荡试验现场实验关键参数统计
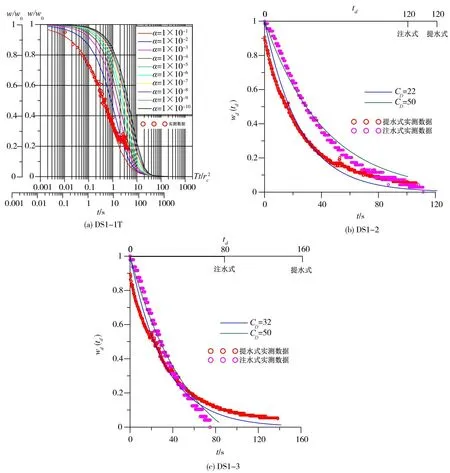
图8 DS1位置3眼监测井中振荡试验无量纲水位恢复曲线配线结果
地质勘察资料显示,龙口市西海岸海水入侵区属滨海平原区,出露地层为新生代第四系,岩性主要为砂、黏性土及少量砾石,监测剖面地质钻探结果显示(见图7),第四系覆盖层厚度范围在61.0~64.0 m。通过现场实施不同层位振荡试验,快速获取了该监测剖面不同埋深含水层渗透系数。
浅部含水层顶板埋深变化范围在4.1~12.4 m、底板埋深变化范围在9.5~13.6 m,利用振荡试验确定含水层渗透系数范围在13.54~127.22 m/d(同一实验井中提水式和注水式振荡试验结果取两者平均值)。浅层地下水监测井中振荡试验实测曲线出现未满足承压非完整井试验特性的主要原因有两方面:(1)地下水监测井按照浅层含水层埋深和过滤器设计埋深相对位置属于承压含水层非完整井,但监测井过滤器与含水层上顶板和下顶板过于接近(DS1-1组现场实验实测曲线与Cooper模型的标准曲线拟合较好);(2)地下水水位埋深接近含水层上顶板,测试井提水后水位瞬时下降,试验影响半径范围内含水层因释水而失去承压特性,相反注水式振荡试验不会造成含水层释水(DS2-1和DS3-1组监测井中提水式振荡试验满足Bouwer&Rice模型)。

图9 DS2位置3眼监测井中振荡试验无量纲水位恢复曲线配线结果
中部含水层顶板埋深变化范围在26.1~29.7 m、底板埋深变化范围在27.6~34.9 m,该地层是龙口市西海岸海水入侵的主要层位,利用振荡试验确定含水层渗透系数范围在35.21~85.81 m/d(同一实验井中提水式和注水式振荡试验结果取两者平均值)。其中DS4-2地下水监测井中水位很长时间都没有恢复到初始状态,渗透系数计算值仅为0.16 m/d,明显不符合地层勘察揭示的含水层介质为砾砂的渗透特征,推测是前期水质采样过程中洗井造成分层止水的黏土下移堵塞了监测井滤水管(花管)。
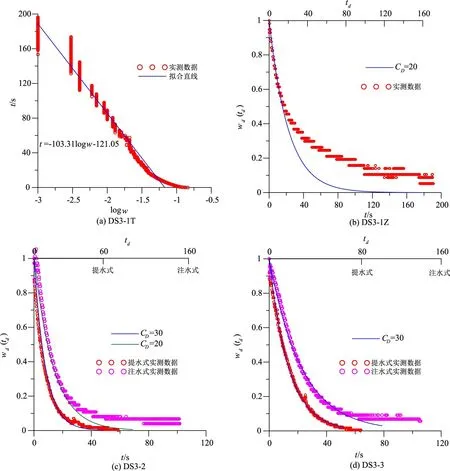
图10 DS3位置3眼监测井中振荡试验无量纲水位恢复曲线配线结果

表5 目标地层渗透系数计算结果
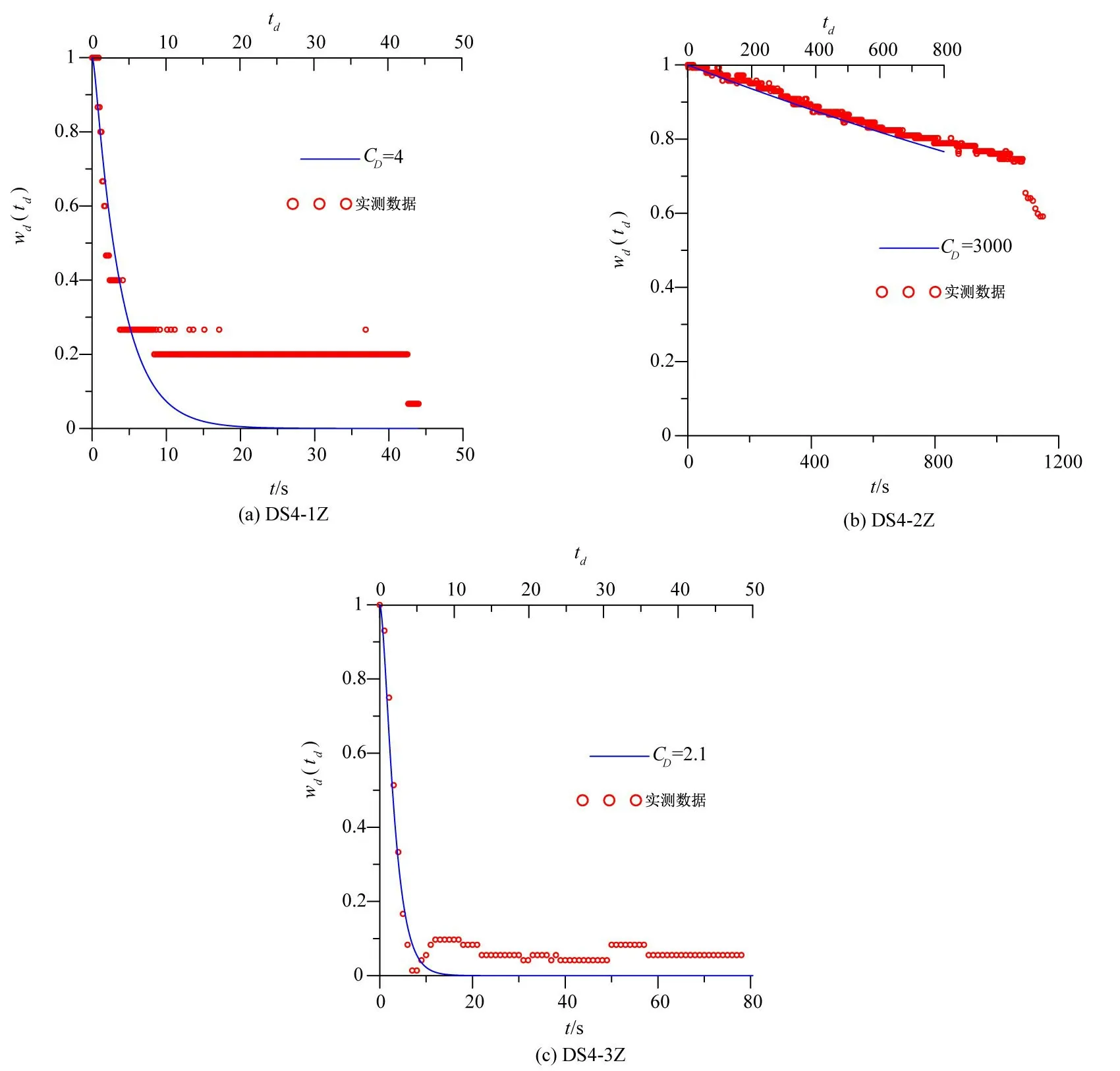
图11 DS4位置3眼监测井中振荡试验无量纲水位恢复曲线配线结果
深部含水层顶板埋深变化范围在46.0~56.7 m、底板埋深变化范围在51.4~59.2 m,利用振荡试验确定含水层渗透系数范围在28.77~125.29 m/d(同一实验井中提水式和注水式振荡试验结果取两者平均值)。其中DS4-3地下水监测井中水位恢复曲线出现了明显欠阻尼振荡,计算的渗透系数值为125.29 m/d,接近粗砂渗透系数参考值的上限。
4 结论
(1)相比于提水式振荡试验,在小孔径地下水监测井中注水式振荡试验更易于实施;提水式振荡试验与注水式振荡试验在确定海水入侵区地层渗透系数时,实验激发方式并没有对试验结果造成明显的影响。需要综合考虑目标含水层类型、测试主井类型、观测井距离、测试井—含水层系统的惯性效应等因素选择合适的振荡试验半解析解模型,生成确定渗透系数参数需要的标准曲线。
(2)室内实验尺度在无法进行抽水试验等条件下利用振荡试验可以快速高效地确定仿真含水层渗透系数,海水入侵砂槽物理模型中实施注水式振荡试验确定了龙口海水入侵区含水层介质(细砂和粗砂)饱和渗透系数,为在滨海含水层现场利用振荡试验确定不同层位含水层渗透性参数提供了重要经验;室内实验受到砂槽模型尺度的影响非常明显,虽然考虑了有限距离定水头边界影响,但尚不能克服有限距离隔水边界的影响。
(3)利用振荡试验在非常短的时间内(单井水位恢复时长大部分在5 min之内)确定了龙口海水入侵区重要监测断面上不同埋深含水层渗透系数,尤其在抽水试验无法顺利实施的地下水监测井中实施了注水式振荡试验,计算的结果与抽水试验的结果接近,因现场实验影响半径的差异部分点位低于抽水试验确定的渗透系数。现场实验结果表明,龙口市西海岸第四系覆盖层中海水入侵主要层位的渗透系数范围在35.21~85.81 m/d,滨海含水层地下水高强度开采条件下高渗透性含水层更易遭受海水入侵。
