基于高阶矩的泄漏电流信号特性分析方法

张宏炯，陈建树*，朱 月，孙永文

（1.国网北京通州供电公司，北京101100；2.北京开元浩海科技发展有限公司，北京100161）

0 引言

低压电网中用电环境复杂，容易发生电击伤亡事故［1］，用户广泛应用剩余电流保护装置，防止人身触电和因泄漏电流造成电气火灾。鉴于在线运行的剩余电流保护装置，大都以供电回路中泄漏电流有效整定值为动作依据，常常出现剩余电流保护装置失效拒动和误动等问题［2］，进而导致剩余电流保护装置的正确投运率较低。低压电网触电故障时泄漏电流特性分析是发现剩余电流保护装置问题和改善工作条件的重要途径，明确供电回路中泄漏电流信号的数字特征，受到了诸多学者的关注。目前，信号通常采用的多种数字特征分析方法［3-6］中，高阶统计量方法可抑制噪声的干扰，计算快速且易于实现，在电力系统检测中成功应用。于九祥［7］从暂态电气信号中提取基频电压和电流，将均值、方差、衰减时间常数等作为表征噪声信号的重要参数。谢尚平等［8］利用高阶统计量对探地雷达数据进行处理，对背景噪声和多次反射波有较好效果。薄远等［9］对几种常见短波通信信号的高阶矩和高阶累积量进行了计算分析。曾孝平等［10］提出了基于三阶累积量的自适应滤波算法，结合对数螺线的变步长机制，实现自适应DME干扰消除。余桐奎等［11］建立基于高阶统计量的舰船瞬态噪声测量分析方法，能够得到瞬态噪声的总能量和特征频谱，解决了舰船典型瞬态工况下水下辐射噪声的测量与分析。关海鸥等［12］应用概率与数学统计量方法，分析了农村低压电网触电电流定量的数字特征。上述文献中采用的高阶统计量方法，为研究低压电网触电故障时泄漏电流特性，明确其时域和频域特征量的变化规律，为提高低压电网供电能力、保障居民用电安全、避免发生电气灾害等奠定技术基础。

1 高阶矩的基本原理

高阶统计量自动抑制任何平稳噪声，既可自动抑制高斯噪声的影响，也能够抑制非高斯有色噪声的干扰。本研究分析触电故障时泄漏电流特性时，高阶矩统计量的定义如下。

设信号p（x）在原点的k阶导数等于X的k阶矩mk，矩生成函数可以唯一地、完全地确定一个概率分布。随机变量X的k阶矩，定义为：

公式（1）～（5）中：E{}∙表示数学期望；p（x）是随机变量x的概率密度。

2 计算泄漏电流高阶矩特征

将文献［12］获取的触电故障时泄漏电流为研究对象，抽取样本数据中触电故障的前5个工频周波和后10个工频周波，共计15个采样周期3 000个点数据。首先依据文献［13］通过快速傅里叶变换计算泄漏电流的直流分量、2～9次谐波分量；定义输入序列点N=200，滑窗步长为1的矩形窗，利用公式（2）计算泄漏电流和触电电流各成分分量的三阶矩，其特征向量曲线变化如图1所示。

图1 泄漏电流与触电电流各成分分量三阶矩特征曲线

图1 是泄漏电流与触电电流各成分分量三阶矩特征曲线，横坐标为采样点，纵坐标为三阶矩的幅值。从图中可得出，泄漏电流与触电电流各成分分量三阶矩特征向量曲线中，泄漏电流的3、5、7次谐波分量的三阶矩的变化幅度较大，在触电故障发生时具有明显的突变点，能准确地反映触电故障发生的时刻；在触电故障发生后10个工频周期内，泄漏电流与触电电流各成分分量的变化趋势较缓，因此在触电故障发生时泄漏电流与触电电流各成分分量的三阶矩特征向量曲线的变化趋势相对一致。

同理利用公式（3）计算泄漏电流和触电电流各成分分量的四阶矩，其特征向量曲线变化，如图2所示。

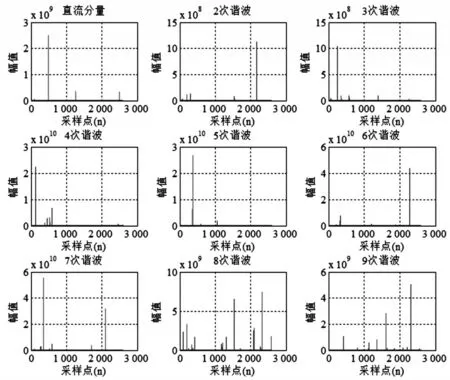
图2 泄漏电流与触电电流各成分分量四阶矩特征曲线

图2 是泄漏电流和触电电流各成分分量四阶矩特征曲线，横坐标为采样点数，纵坐标为特征量幅值。从图中可得出，泄漏电流与触电生物电流各成分分量四阶矩特征曲线变化趋势较为平坦，曲线整体变化趋势普遍趋于零，其值域范围变化较大；两种电流各成分分量的四阶矩特征向量曲线大都存在突变点，泄漏电流的直流分量、5、7、8、9次谐波分量存在突变点，但突变点不能反映触电故障的发生时刻，偶数次谐波分量的四阶矩特征向量曲线存在相对较大的相关性。

同理利用公式（4）计算泄漏电流和触电电流各成分分量的五阶矩，其特征向量曲线变化，如图3所示。

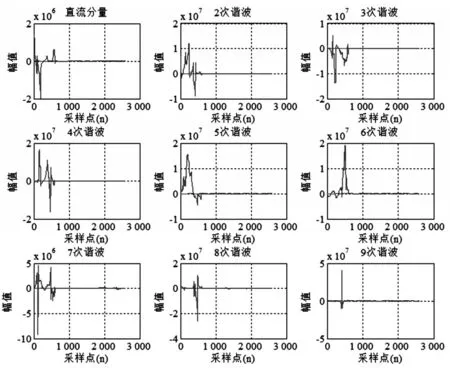
图3 泄漏电流与触电电流各成分分量五阶矩特征曲线

图3 是泄漏电流和触电电流各成分分量五阶矩特征曲线，横坐标为采样点，纵坐标为特征量幅值。从图中可得出，泄漏电流与触电电流各成分分量五阶矩特征曲线的变化趋势较为一致，其值域范围变化幅度较大，在触电故障发生时刻，有较为明显的突变点；触电故障后10个工频周期内，泄漏电流与触电电流各成分分量的五阶特征曲线变化趋势较为平稳，无明显变化。

同理利用公式（5）计算泄漏电流和触电电流各成分分量的六阶矩，其特征向量曲线变化，如图4所示。

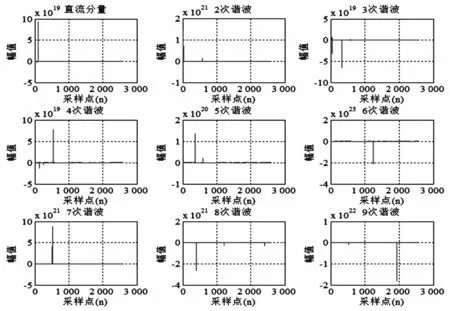
图4 泄漏电流与触电生物电流各成分分量六阶矩特征曲线

图4是泄漏电流与触电生物电流各成分分量六阶矩特征曲线，横坐标为采样点数，纵坐标为特征量幅值。从图中可得出，泄漏电流与触电电流各成分分量的六阶矩特征向量曲线变化趋势较为平稳，普遍趋于零点附近；两种电流各成分分量六阶矩特征向量值域波动幅度较大；泄漏电流与触电电流各成分分量的六阶矩特征向量曲线存在较为显著的突变点，但其突变点不能反映触电故障发生时的暂态变化。

3 结果与分析

为进一步明确其时频域特征量的变化规律，通过计算发生触电故障时电气信号的高阶矩特征，统计分析泄漏电流和触电电流的直流分量，以及2～9次谐波分量的高阶矩特征曲线的极大值点，如表1所示。

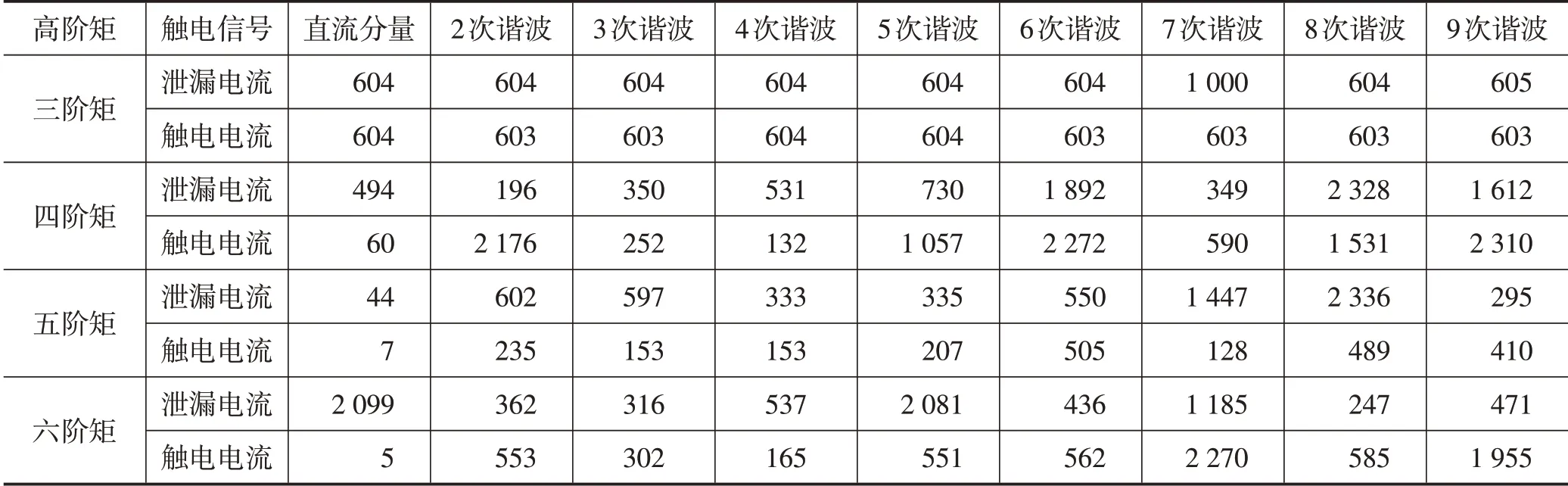
表1 泄漏电流与触电电流各分量高阶矩特征的极大值统计

表1是泄漏电流与触电电流的直流分量、2～9次谐波分量的高阶矩特征曲线的极大值点。三阶矩特征向量的极大值点中，偶数次谐波分量的极大值点相对统一，奇数次谐波分量的极大值点重合度较低。四阶矩特征向量的极大值点中，泄漏电流与触电电流的偶数次谐波分量的四阶矩特征向量曲线的极大值点较为统一，表明偶数次谐波分量存在较强的相关性，奇数次谐波分量的相关度较小。五阶矩特征向量的极大值点中，偶数次谐波分量的极大值点较为统一，其中4次谐波分量、5次谐波分量、6次谐波分量重合度较高。同样六阶矩特征向量曲线的极大值点中，偶数次谐波分量的极大值点一致性好，泄漏电流与触电电流各成分分量的六阶矩特征向量的极大值点重合率普遍较低，不能反映触电故障发生时刻极值点变化情况。所以三阶矩中泄漏电流与触电电流特征曲线存在较为显著的突变极大值点，且极大值点的重合率较高，因此当触电故障发生时，高阶矩中的三阶矩能较好地反映泄漏电流与触电电流的特征值变化情况。

针对泄漏电流与触电电流各分量的高阶矩，采用相关性分析计算特征曲线的相关系数平均值，以便更好地说明其相关性，因此可得泄漏电流与触电电流各分量高阶矩特征的平均相关系数，如表2所示。

表2 泄漏电流与触电电流各分量高阶矩特征的平均相关系数

表2是泄漏电流与触电电流的直流分量、2～9次谐波分量的高阶矩特征曲线的相关系数平均值。两种信号各分量的三阶矩特征向量曲线呈现显著相关性，并且偶数次谐波分量的相关性系数高于奇数次谐波分量。泄漏电流与触电电流各分量的四阶矩特征向量曲线呈现较低相关性。五阶矩特征向量曲线的相关系数平均值中，偶数次谐波分量的相关性较高，奇数次谐波分量的相关性较小。六阶矩特征向量曲线的相关性平均值较小，其中2次谐波分量的相关系数最大仅为0.005 9，但其相关系数平均值较小，不能作为利用剩余电流的特征向量预判触电生物电流特征向量的指标。

4 结语

本研究利用高阶矩中的三、四、五、六阶矩，计算泄漏电流与触电电流的直流分量、2～9次谐波分量的统计量特征，相关分析结果如下。

（1）高阶矩中的三阶矩能较好地反映供电回路电气信号的特征值变化情况。在触电故障发生时刻，泄漏电流与触电电流特征向量曲线存在较为显著的突变极大值点，且极大值点的重合率较高，其相关性系数普遍大于0.85。

（2）从四阶矩和六阶矩的分析结果可以得出，四阶矩及六阶矩特征向量曲线存在多个突变点，极大值点通常分布在触电故障发生后10个工频周期内，且剩余电流与触电生物电流四阶矩和六阶矩的特征向量曲线的相关系数较小呈现较低相关性，相关系数普遍不超过0.000 3。

（3）泄漏电流与触电电流各成分分量三、四、五、六阶矩的特征向量中，偶数次谐波分量的高阶矩特征的相关性普遍高于奇数次谐波分量。高阶矩特征随着阶数的增高其对应的值域变化幅度也对应增大，两种电气信号各分量的相关系数平均值最高的是三阶矩，其次是五阶矩；四阶矩和六阶矩的特征向量相关性较低，呈现的相关度较弱。

所以通过高阶矩中的三阶矩和五阶矩特征曲线，能较好地反映出触电故障时刻，以及触电信号特征向量的幅值变化情况。触电故障发生后的10个工频周期内，泄漏电流与触电电流的三阶矩的特征向量幅值无显著突变点，二者特征向量曲线变化趋势较为统一，特征向量曲线的相关系数较高，呈显著相关性，进而为利用高阶矩统计量改进剩余电流保护装置性能提供技术参考。