外磁场下的双层类石墨烯系统的元激发能谱
2020-12-11赵宇星成泰民
赵宇星, 成泰民,2
(1.沈阳化工大学 材料科学与工程学院, 辽宁 沈阳 110142;2.沈阳化工大学 理学院, 辽宁 沈阳 110142)
二维石墨烯发现之前,Mermin和Wagner从统计力学推导发现了“任何具有连续对称性的二维热力学系统,在有限温度下,其连续对称性不可能发生自发破缺”,此为Mermin-Wagner定理.自然界不存在天然的石墨烯,但是室温下人工可以制备石墨烯,且其结构稳定.这成为二维单原子层材料的研究热点,主要是由于此种材料具有独特的结构与性能,在纳米电子器件、能源与生物等领域都有广泛的应用前景.材料中引入各向异性、晶格空位缺陷[1-2]、吸附另种元素[3-4]、边缘化[5-9]和掺杂[10-12]可以破缺二维材料的连续对称性.文献[1-2]报道,当2个单空位缺陷位于相同的六角子晶格,则产生铁磁性耦合;反之,当2个单空位缺陷位于不同的六角子晶格,则产生反铁磁性耦合.因此,类石墨烯材料在有限温度下的奇异的物理性质引起科学家们的关注[3,10-13].掺杂可以调节石墨烯的费米能级,同时可以在一定程度上打开石墨烯的带隙.如果能打破这两层的反向对称,就可以得到非零带隙.近年来,经过不断探索,人们发现通过静电效应掺杂或异质化学掺杂方法可以有效地打开双层石墨烯带隙,但是外磁场下双层类石墨烯体系研究鲜有报道.为此,我们对双层类石墨烯体系在外磁场下的元激发谱和能隙变化规律进行研究.
1 磁性双层类石墨烯系统
磁性双层类石墨烯系统如图1所示,体系由A、B、C、D四种子晶格构成.A和B构成上层,C和D构成下层,每种子晶格都含N个原子.上层中最近邻两种原子A和B的层内耦合是铁磁性交换耦合,JAB=J1(>0);下层中最近邻两种原子C和D的层内耦合是铁磁性交换耦合,JCD=J2(>0).A和C之间层间反铁磁性耦合为JAC=J3(<0);B和D之间层间反铁磁性耦合为JBD=J4(<0).上层层内、下层层内和层间各向异性分别用D1、D2和D⊥表示,并令A、B、C、D四种子晶格中原子自旋分别为S1、S2、S3和S4.外磁场以h=gμBH表示.
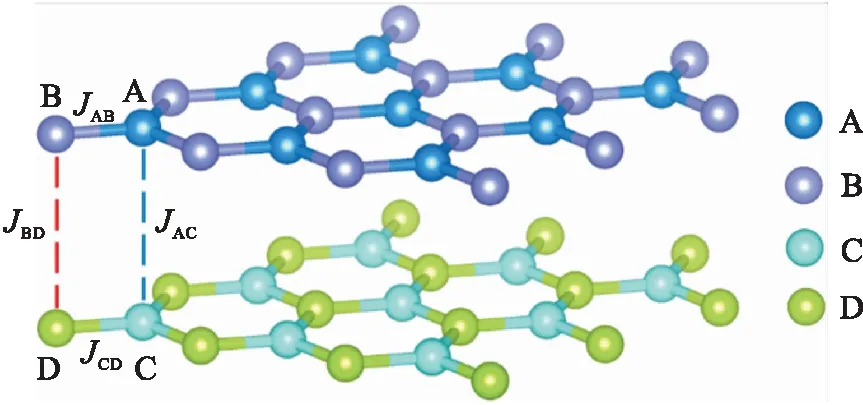
图1 磁性双层类石墨烯系统的磁性交换作用示意图
2 磁性双层类石墨烯的模型体系元激发谱
按图1及各向参数,建立体系Hamiltonian如下:
(1)
对式(1)利用自旋升降算符表示如下:
(2)
对式(2)的自旋算符进行线性霍斯坦因-普利马可夫(H-P)变换如下:

(3)
把式(3)代入到式(2),并只留至2次幂算符的线性项可得
(4)
其中:
E0=-6N(J1+D1)S1S2-
6N(J2+D2)S3S4+2N(J3+D⊥)S1S3+
2N(J4+D⊥)S2S4-
hN(S1+S2-S3-S4).
(5)
对式(4)中的自旋偏离产生与湮灭算符进行点阵傅里叶变换
(6)
(7)
对式(7)整理可得
(8)
其中:
(9)
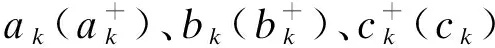
(10)
其中:
(11a)
(11b)
βk=eikzc,β-k=e-ikzc.
(11c)
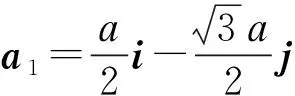
(12a)
(12b)
(12c)
类石墨烯结构的第一布里渊区示意图如图2所示.

图2 类石墨烯结构的第一布里渊区
(13)
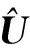
(14)
式(13)可以表示为
(15)
对体系哈密度量建立IEO方程:
(16)
其中τAσ、τBσ、τCσ和τDσ是复数.
由式(13)—(16)可得
(17)
其中:
(18)
(19)
从而由式(17)—(19)可得
(20)
求解式(20)得久期方程[14],可得双层类石墨烯系统的元激发能量.
四次方程的判别式为
(21)
当Δ≥0时,四次方程实根如下:
(22)
其中:
(23)
因为k1k2k3=-β1,所以当β1>0取:
(24a)
当β1<0取:
(24b)
(25)
(26)
(27)
(28)
其中:
(29)
3 数据分析及讨论
根据式(22)—(29)研究外磁场下的双层类石墨烯系统的元激发能谱的变化规律.
有外磁场时、无外磁场时双层类石墨烯系统的元激发能谱在第一布里渊区的色散分别如图3、图4所示.
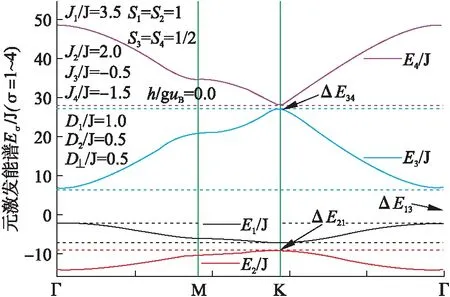
图3 无外磁场时双层类石墨烯系统的元激发能谱在第一布里渊区的色散
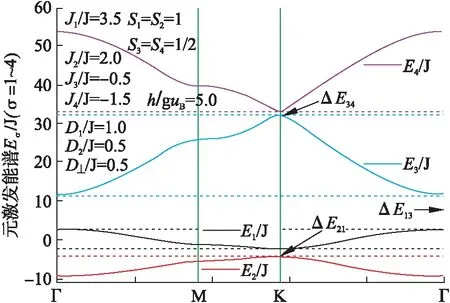
图4 有外磁场时双层类石墨烯系统的元激发能谱在第一布里渊区的色散
由图3和图4可知,双层类石墨烯系统的元激发能谱出现了3个带隙ΔE21、ΔE13和ΔE34.比较图3和图4可知,外磁场只起到蒋双层类石墨烯系统的元激发能谱向高低能级平移的作用.带隙ΔE21和ΔE34出现在K对称点上,而带隙ΔE13出现在Γ对称点上.因此,利用如下公式表示上述3个带隙.
(30)
可以利用式(30)具体研究各项物理量对体系带隙的影响.综上,由各向同性体系磁振子谱无带隙相比较可知,在双层类石墨烯系统因其连续对称性破缺,引起了体系带隙.
4 结 论
对双层类石墨烯系统元激发能谱的研究得到了如下结果:
(1)双层类石墨烯系统的元激发能谱出现了3个带隙ΔE21、ΔE13和ΔE34.
(2)外磁场只起到将双层类石墨烯系统的元激发能谱向高低能级平移的作用.
(3)带隙ΔE21和ΔE34出现在K对称点上,而带隙ΔE13出现在Γ对称点上,并导出其表达式.
(4)在双层类石墨烯系统因其连续对称性破缺,引起了体系带隙.
(5)IEO方法求解双层类石墨烯系统的元激发能谱,相对于推迟格林函数方法的封闭运动方程链或者幺正变换,求解方便、思路清晰简捷,IEO算子满足封闭加法群.
