善用多元表征 优化数学教学
2020-12-10成爱梅
成爱梅
摘 要:多元表征是数学学习的重要方法之一,根据多元表征的方式和学生认知水平的发展规律之间的联系,设计合理的数学活动,积累抽象的活动经验是基于数学核心素养教学设计的要求。文章从“丰富多元表征,尊重个体差异”“层次化多元表征,依从认知顺序”“互动多元表征,互补认知过程”“系统化多元表征,完善认知结构”四个方面,具体阐述怎样使用多元表征优化小学数学教学。
关键词:多元表征;认知;个体差异
多元表征指对同一对象使用文字、图像、语言或具体物等多种形式阐明事物的基本特征。数学教学中常用来刻画对象的多元属性,通过表征的相互联系、渗透和转换帮助学生深刻理解数学对象的内涵,构建新的认知结构 [1]。学生的认知结构存在着个体差异,对同一知识的学习在心理活动过程中呈现的方式不一样,表征方式也不尽相同。一般数学问题都具有抽象性和复杂性,单一的表征仅能关注到问题的一面,无法准确地理解问题的本质。多元表征则能深入问题的内部结构,优化教学效果,提高学生的数学核心素养。
一、丰富多元表征,尊重个体差异
学生对问题的表征能力直接影响着解决问题的能力,我们不得不承认在“以人为本”的现代化教学理念下,每个学生受遗传、学习和生活经验的影响,都会形成自己独特的个性特征。这种个体差异使学生遇到同一问题时,表现出不一样的心理活动过程,在小学数学的学习中表现尤为显著。
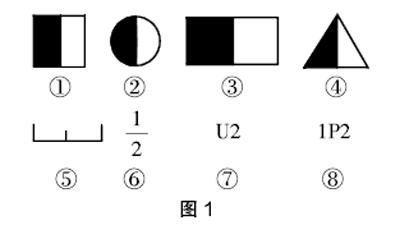
例1:“分数的初步认识”,用自己的理解表述 。
① ② ③ ④
U2 1P2
⑤ ⑥ ⑦ ⑧
学生根据自己的认知结构,呈现出自己理解的 。从表征结果(图1)可见:每个学生因原有的知识结构和生活经验不一样,表征 的方式也不一样。想最小化 的学习障碍,最大化 的学习成效,教师可将学生表征的内容用小组合作学习的方式,鼓励学生将自己理解的 和小组成员理解的 互相联系并转换,用更丰富的多元表征方式来表达对 的理解,从而更深刻地认识,而不是简单地把知识灌输给学生。学生的表征过程也是构建知识的过程,教师鼓励学生从自己的表征与同学的表征中寻找共同的内部关系,就是强化概念的过程。这样不仅帮助学生深度理解了 这个抽象的概念,还尊重了学生的个体差异,合理运用多元表征的形式互换,促使不同水平的学生在原有知识的基础上都获得发展。
二、层次化多元表征,依从认知顺序
个体从出生到成熟,其认知结构与环境互相作用、不断重构,不可逆地经历“动作感知——前运算——具体运算——形式运算”的过程。小学阶段的学生主要处于第三阶段(具体运算)和第四阶段(形式運算)两个阶段。具体运算阶段的学生思维具有较大的易变性,能进行简单的逻辑分类解决守恒问题;形式运算阶段的学生思维逐渐接近于成人,能实现“假设演绎推理——进行正确评价——形式推理——解决逻辑问题”的过程 [2]。运用多元表征开展教学常出现失败的原因主要集中在教师没有把握学生认知发展的规律,以偏概全地引导学生机械表征,缺乏各种表征间的联系,致使学生的认知顺序出现了混乱或颠倒。因此,教师可根据学生的认知规律,遵循其心理活动特征,开展层次化多元表征的教学模式实现意义教学,优化数学课堂。
例2:“相差数量关系”,运用多元表征“6比4多多少”。
从多元表征的层次出发,教师可安排如下活动:
(1)体验表征:组织学生通过摆放橡皮和铅笔的方法,比较数字4和6的数量关系。引导学生边摆放、边思考:如果第一行摆放4只橡皮,第二行应该先摆放几只铅笔,然后再摆放几只铅笔?它们之间有怎样的关系?
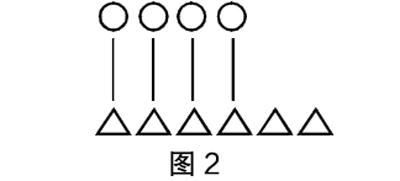
(2)图像表征:组织学生在草稿纸上画 和 ,第一行画4个 ,第二行对应画6个 (见图2),通过对比分析表征6和4的数量关系。
(3)语言与符号表征:鼓励学生用式子表征6和4的数量关系。
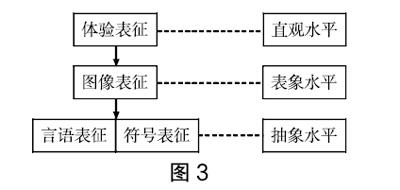
操作完成后,让学生根据自己摆放的过程去思考:在第一轮摆放橡皮和铅笔的时候,先摆放橡皮还是铅笔?为什么要这么摆放?我得出了怎样的结论?学生因动手操作亲历摆放过程,所以对这部分内容的直观印象会比较深刻。第二轮,学生用绘图的方式表示了6和4的数量关系,在此鼓励学生用语言将自己的绘图表征出来,体现学生的图像表征能力。第三轮,在前两轮的基础上,思维得到了相应的拓展,让学生用式子(符号)将6和4的数量关系表现出来,此时学生的感知会上升到抽象水平。归纳学生的认知发展和表征的层次对应如下图(见图3):
因此,层次化多元表征时应遵循学生认知水平的阶段性,根据表征内容设计由低级到高级、部分到整体的操作过程,有序构建知识框架,实现学生思维从直观水平到表象水平,再到抽象水平的成长。
三、互动多元表征,互补认知过程
个体的经验受综合因素的影响对事物的理解各不相同,存在着一定的局限性。利用多元表征的互补性,引导学生通过积极的互动完善认知过程是建构主义者所倡导的一种教学方式。学生在活动中将自己的表征与同伴的表征加以对比,取其精华去其糟粕,不断修正、完善自己的认知。因此,教师应多创造合作交流的平台,让学生在取长补短、互相学习中共同提高。
例3:“组合图形的面积”,请求出以下图形(见图4)的面积。
学生根据自己的认知经验,得出如下不同的解决方法(见图5):
图5的解题思路可归纳为分割法、割补法和添补法三种,不管使用哪种方法,最终都达到了求出图形面积的目的。教师可引导学生观察同伴的表征方式与自己的方式进行对比,思考哪种方法更加简单直接,学会借鉴别人的表征方式,通过互动完善自己对问题的认知。互动多元表征能弥补个体的不足,促使學生开拓思维,从多角度认识问题并分析问题。
四、系统化多元表征,完善认知结构
现代化的课堂教学不只追求学生对理论知识的掌握程度,更关注学生的认知过程。完整的认知过程是伴随在心理活动中的心理特征,指人由表及里、由现象到本质地认识客观事物。面对数学问题,学生可凭借自己的经验产生不同的心理活动,做出相应的判断,这是个体根据自己的经验对问题不同层面、不同角度做出的反应。不论原有的认知水平如何,最终达到的学习目标都是一致的。学生的多元表征能力和学生的认知成正比关系。因此,教师要引导学生理论联系实际系统化多元表征问题,完善认知结构。
例4:“分数的初步认识”,构建 的完整认知。
教师可从体验表征、图像表征、言语表征和符号表征四个方面引导学生认识 。首先,让学生通过折纸、剪纸、倒水或涂色等实际操作来体验表征 ;其次,鼓励学生用绘制不同的图形来表示 ,形成图像表征;再次,鼓励学生用语言表征,如“把一块蛋糕平均分成两份,那其中的一份蛋糕就是这个蛋糕的 ”;最后,使用一些特定的符号来表示 ,如图1中的U2、IP2等。以上四种方法互相联系、相互补充的目的都在于表征 这个分数,不断完善学生对 的认知。
这四种表征方式关系图(见图6),明确地展示出了数学信息与四种表征方式之间错综复杂却有章可循的关系。多元表征是使用各种方式表达同一个数学信息的过程,也是学生面对数学信息时思维和心理活动过程。它不仅能丰富信息的本质和外延,还是各种表征形式的互相完善与补充。
总而言之,在当下这个专业分工细化、信息生产爆炸的时代,通过层次化、系统化的多元表征为学生构建新的认知系统,为培养数学思维和提高解题能力提供了有效的途径。
参考文献:
[1] 刘加霞. 利用学习的多元表征方式促进学生对算理的“真理解”[J]. 小学教学(数学版),2010(03).
[2] 吕程,周莹,唐剑岚. 多元表征:探寻数学智慧课堂的一把密钥[J]. 教育与教学研究,2012(06).
