最值难入手 转化显威力

◇ 安徽 蔡 赫 汪庭斌

最值问题一直是高考的热点内容,几乎每年必考,且常考常新.这类问题最能考查考生的综合素质,体现出高考的区分度.解决这类问题往往需要学生具备多方面的数学核心素养,包括数学逻辑推理、数学运算、数学建模等,故这类问题常作为压轴题型出现.而且此类问题,考生并不能通过大量的训练(也就是题海战术)获得解决思路,需要一定的数学思想作为引导.本文旨在为学生解决最值问题提供一些通用可行的方法,为高三二轮专题复习中函数压轴小题的解决提供一些解题方向.为达到这个目的,笔者特选取了一道典型的高考真题,从三个角度(函数、几何、不等式)进行解题.在不同的解题角度里,又以不同的方法切入,充分考虑到不同学生的基础与水平.另外,为体现高考选拔的要求,以及初等数学与高等数学的衔接,本文使用了函数的凹凸性作为其中一种解法,并对凹凸性的定义给出了解释.

试题(2018年全国卷Ⅰ理)已知函数f(x)＝2sinx＋sin 2x,则f(x)的最小值是________.

分析本题是一道最值问题,但不同于以往的单元或多元最值问题,而是以三角函数为载体,在问题解决上既可以从函数角度入手,也可以从三角函数性质入手,还可以从图象入手,体现了高考试题入口宽的特点.

相关知识对于函数问题,尤其是涉及三角函数,要养成分析其性质的习惯(奇偶性、周期性、单调性等),从周期性入手,利用诱导公式得f(x＋2π)＝2sin(x＋2π)＋sin 2(x＋2π)＝2sinx＋sin 2x,即f(x＋2π)＝f(x),故f(x)的周期为2π;从奇偶性入手,有f(－x)＝－f(x)(x∈R),为奇函数,故根据奇函数性质可以得到fmax(x)＋fmin(x)＝0,再结合三角函数的正负号,综合以上性质,我们只需要考虑[0,内的函数性质.

1 函数角度

转化为同角,化归为一元函数,利用导数来求解.

思路1利用二倍角公式,化归为同角问题.

解法1由题可得f′(x)＝2cosx＋2cos 2x(0≤利用二倍角公式和因式分解,可得f′(x)＝2(cosx＋1)(2cosx－1).在内,cosx＋1＞0恒成立,故f′(x)的符号只和2cosx－1的符号有关,结合图象很快得到在内f′(x)＞0,在内f′(x)＜0,故时,f(x)取得最大值由奇偶性可知f(x)最小值为.

思路2利用半角公式,化归为同角问题.

解法2由题可得f(x)＝2sinx(1＋cosx),又,则f(x)可变形为再利用平方代换和万能公式代换即可化为一个角的函数关系这里的次数过高,为防止计算和求导出错,采用换元法后再求导,其实也是一种转化和化归的思想.令故可得这样就化归为很典型的求导求最值问题,学生就可以自行解决了.求得导数为时,所以时,y取最大值则f(x)取最大值由以上分析知最小值为.

思路3利用弦切互换,化归为同角问题.

解法3分子分母同时除以,得

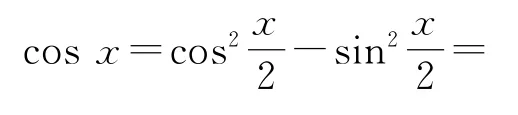
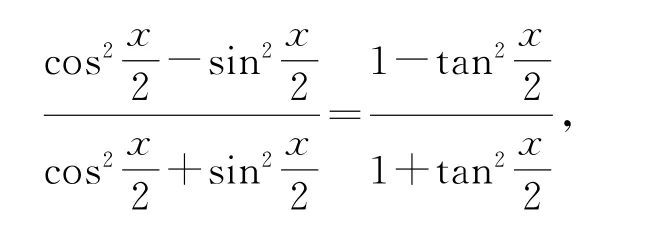
原函数f(x)＝2sinx(1＋cosx)即可化归为

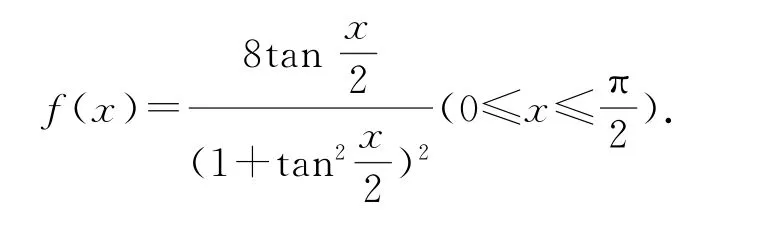
下面再利用换元法即可化归为常见的一元函数求最值问题,利用导数即可解决.令,则0≤,则

思路4利用平方代换,化归为同角问题.

解法4f(x)＝2sinx(1＋cosx),则

再令t＝cosx,t∈[0,1],则可转化成函数y＝4(1－t2)(1＋t)2(0≤t≤1),下面即是常规的利用导数求最值问题,求导得

以上这几种方法均是从函数角度入手,利用代数变形等手段,将问题转化为常规的一元函数问题,可以说是解决最值问题的通法,教师应该多辅以此方面的训练,以便学生理解掌握此类通法.

2 几何角度

化归为图形,几何法求解.

思路5引入变量,化归为线性(非线性)规划问题.

解法5在此令m＝sinx,n＝1＋cosx,则有如下关系:m2＋(n－1)2＝1,其中0≤m≤1,1≤n≤2,设z＝2mn,这样问题就化归为如下问题:已知求z＝2mn的最值问题.可进一步换元,即已知求z＝2xy的最值,这是学生常做的一种非线性规划问题.由图1可知,当双曲线圆x2＋(y－1)2＝1在第一象限相切时z取最大值,联立得消去y得x4－2zx＋z2＝0,此方程在0≤x≤1内只有一个解,令g(x)＝x4－2zx＋z2,求导得g′(x)＝4x3－2z,令导数为0可得解得z＝因此f(x)的最大值为最小值为.

图1

思路6利用单位圆,化归为面积问题.

解法6利用三角函数的定义,在单位圆上取一些特殊的点,将的表达式转换为面积问题.如图2,以原点为圆心作一个单位圆,在此圆上取三个点A(－1,0),B(cosx,sinx),C(cosx,－sinx),则有BC＝2sinx,A到BC的距离为1＋cosx,因此有

故f(x)＝2S△ABC,这样就将问题转化为求△ABC面积的最值问题,而圆的内接三角形中,正三角形面积最大,这个圆的半径为1,其内接正三角形边长用正弦定理即可求出,设其边长为a,由正弦定理可知则故其面积为则f(x)最大值为所求最小值为.

图2

以上方法是寻找代数表达式背后的几何背景,这需要合理的联想和一定的技巧,再加上一些经验的积累.以本题来说,从f(x)的表达式中的乘积关系联想到几何中的面积表示,再从三角函数联想到单位圆,最后通过一些合理的构造得到一个△ABC,并且其面积刚好和f(x)有关,最终将问题解决.

3 不等式角度

转化为等式,化归为定值,不等式法求解.

思路7利用半角公式,化归为不等式问题(借助均值不等式).

解法7根据前面方法2的分析,可知f2(x)＝对这个式子进行拆分凑出可以使用均值不等式的形式

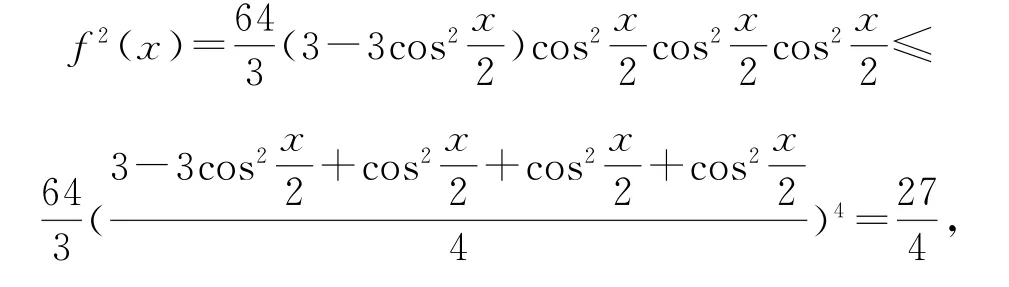
思路8利用数字1,化归为不等式问题(借助柯西不等式和基本不等式).

解法8由题意可知

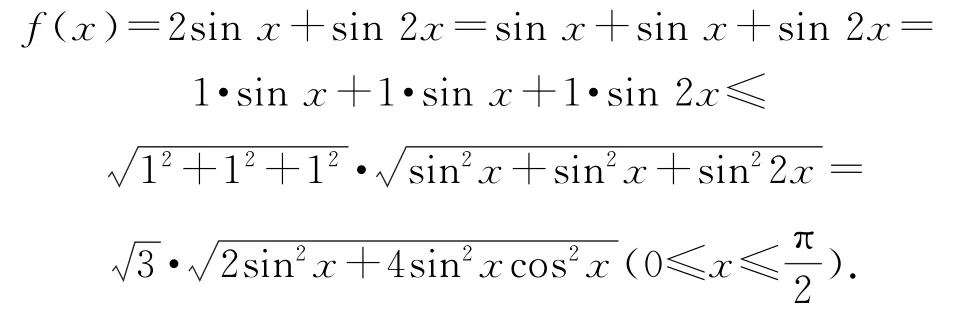
再利用基本不等式得

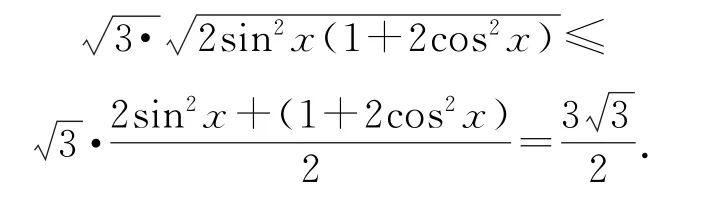
思路9利用函数的凹凸性,化归为不等式问题(借助琴生不等式).

解法9这里先给出函数凹凸性的导数判断法:对于实数集上的函数y＝f(x),若它的二阶导数存在,且在区间[a,b]上f″(x)＞0,就称这个函数在区间[a,b]上为凸函数,反之为凹函数.

琴生不等式定义:若f(x)在区间[a,b]上为凸函数,则对任意的x1,x2,x3,…,x n∈(a,b),有不等式当且仅当x1＝x2＝…＝x n时等号成立.反之若f(x)在区间[a,b]上为凹函数,则对任意的x1,x2,x3,…,x n∈ (a,b),有不等式,当且仅当x1＝x2＝…＝x n时等号成立.

利用凸函数定义易判断在[0,π]上,y＝sinx为凸函数,我们先对题目的函数解析式f(x)＝2sinx＋sin 2x进行转化变形(这里我们利用诱导公式)可得f(x)＝sinx＋sinx＋sin(π－2x),再利用琴生不等式可以得到如下的不等式:

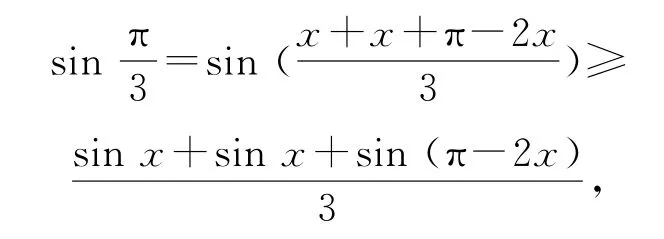
当x＝π－2x时,即时取等号,故可求出f(x)的最大值为,故所求最小值为.

以上的几种方法均是从不等式角度入手来解决最值问题,通过合理的变形、配凑将表达式转化为可以使用一些常见不等式的形式,由于其构造的技巧性较强、局限性也较大,需要长期的经验和技巧积累、扎实的数学基本功和对数学式子的敏锐直觉.

本文所述的三种视角(函数、几何、不等式)是高中阶段解决最值以及范围问题的三大方向,一般情况下,如果题目只涉及一元变量,我们常用的就是函数思想,将问题化归为一元函数问题,其中可能会利用一些代数变形等手段进行转换;如果涉及的是二元甚至更多元的情况,我们优先考虑能否将多元转化为一元,再化归为函数问题;如果上述两种方法行不通或者求解过程太过复杂,再考虑利用几何和不等式手段来解决问题.不论是哪种手段都需要转化和化归思想作为引导,可谓是最值问题难入手、转化化归显威力、函数变形是通法,几何、不等式来辅助.