函数创新性问题赏析
2020-12-09浙江王茂聪
◇ 浙江 王茂聪
函数是数学大厦的基石,也是高中数学的核心内容.高考对函数的要求一向很高,除了要求考生掌握基本问题的解法外,往往还渗透一些创新性问题,这类问题既考查了考生融会贯通的综合能力,同时也检验了考生勇于探究的学习品质.这类问题新颖独特,本文列举几例,与大家共赏.
1 三次函数拐点的应用
三次函数是最常见的高次函数,也是高考命题经常涉及的函数.而三次函数拐点的概念,在中学教材中未曾提及,题目中给出函数的概念,并要求学生利用这个概念解决相关问题,可以全面考查学生的学习力.
例1对于三次函数f(x)=ax3+bx2+cx+d(a≠0),给出如下定义:
设f′(x)是函数y=f(x)的导数,f″(x)是函数f′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.
某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.给定函数
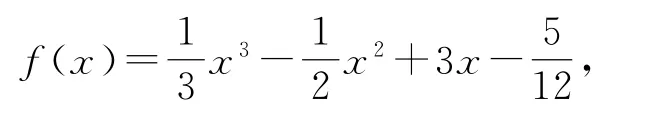
请你根据上面探究结果,计算
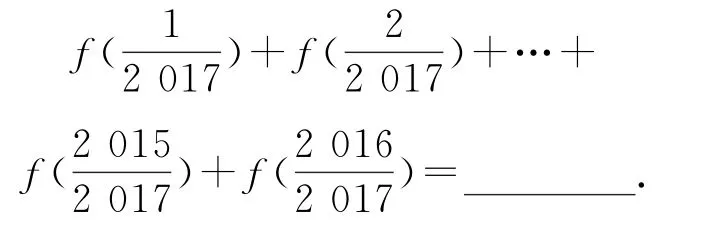
解析
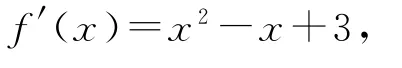
故f″(x)=2x-1.
令f″(x)=0可得,所以函数f(x)的拐点即对称中心为(),若x1+x2=1,则

所以

点评
本题属于背景新颖的材料分析题,要求考生从材料中读取有关信息,解决问题.本题既考查了导数的应用,又考查了三次函数的对称性,题干创新独特,能灵活考查学生利用数学知识解题的本质,即转化思想.
2 抽象函数值的大小比较
抽象函数是高中函数的难点,与抽象函数有关的不等式问题一般会涉及函数的单调性,而抽象函数的单调性又与导数有着密切的联系,于是这种综合性极强并要求考生具有构造思想的数学问题应运而生.
例2设函数f(x)的导函数为f′(x),对任意x∈R都有f(x)>f′(x)成立,则( ).
A.3f(ln 2)<2f(ln 3)
B.3f(l n 2)=2f(l n 3)
C.3f(ln 2)>2f(ln 3)
D.3f(l n 2)与2f(l n 3)的大小不确定
解析
由题意对任意x∈R都有f(x)>f′(x),所以g′(x)<0,即g(x)在R上单调递减.
又由l n 2<l n 3,可知g(l n 2)>g(l n 3),即

点评
抽象函数值的大小比较既是一类新颖题,又是一类难题.恰当构造函数,并利用函数的单调性比大小是解决这类问题的通法.本题求解的关键是利用已知条件构造恰当函数,考查了对数运算公式的应用.
3 新定义函数问题
新定义问题是数学中最常见的创新题,新定义函数问题给出一个函数的新名称,同时给出该函数独特的性质,要求考生利用新函数的新性质去解决相关问题.
例3若函数f(x)是定义域D内的某个区间I上的增函数,且在I上是减函数,则称y=f(x)是I上的“单反减函数”,已知f(x)=l nx,.
(1)判断f(x)在(0,1]上是否是“单反减函数”;
(2)若g(x)是[1,+∞)上的“单反减函数”,求实数a的取值范围.
解析
(1)由于f(x)=l nx在(0,1)上是增函数,且,因为
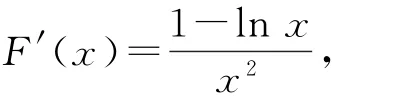
所以x∈(0,1)时,F′(x)>0,F(x)为增函数,所以f(x)在(0,1)上不是“单反减函数”.

因为g(x)是[1,+∞)上的“单反减函数”,则g′(x)≥0在[1,+∞)上恒成立,所以g′(1)≥0,即在[1,+∞)上是减函数,所以G′(x)≤0在[1,+∞)上恒成立,即在[1,+∞)上恒成立,即axaxl nx-4≤0在[1,+∞)上恒成立.
令p(x)=ax-axl nx-4,求导得
p′(x)=-alnx≤0,
故p(x)=ax-axl nx-4在[1,+∞)上是减函数,pmax(x)=p(1),由p(1)≤0得a≤4.
综上,a的取值范围为[0,4].
点评
本题的新颖之处是给出新定义“单反减函数”,考查学生对新定义的认识;其次,本题需要利用导数解决新定义函数的有关问题,考查新定义的应用.本题表面上看是函数新问题,但解决此问题的方法还是研究函数单调性的老方法——导数法.可谓“以旧破新”.
创新,是一个民族的灵魂,也是数学的灵魂.数学教育要创新,数学问题也要创新,这是中学数学发展的必由之路,也是培养数学创新思维的有效途径之一.
