小议“构造函数”巧解不等式
2020-12-09山东李百玲
◇ 山东 李百玲
提升学生高中数学能力,除了掌握必要的基础知识,更重要的是学生对数学思想方法的灵活运用.函数与方程、转化与化归是高中数学中比较重要的两大思想,而构造函数的解题思路恰好是这两种思想的良好体现.
在近几年高考数学试卷中,许多与函数相关的解不等式的题目,尤其是压轴小题,经常能用到构造函数法.所谓构造函数是指通过一定方式,设计并构造一个与待解答问题相关的函数,并探究其单调性,借助图象或利用运算结果,从而得到不等式的解集.本文重点探讨如何合理地构造函数.
1 构造f(x)与x的关系
当题目所给的不等式中除了f(x)外,仅含有x,常用的构造形式有.对于xf′(x)+f(x)>0,构造h(x)=x f(x);对于x f′(x)-f(x)>0,构造.
例1设f(x)是定义在R上的偶函数,当x<0时,f(x)+x f′(x)<0,且f(-4)=0,则不等式xf(x)>0的解集为________.
解析
设F(x)=x f(x),则有F′(x)=f(x)+xf′(x),当x<0时,f(x)+xf′(x)<0,F′(x)<0,所以F(x)在(-∞,0)上单调递减.因为f(x)为偶函数,x为奇函数,所以F(x)为奇函数,故F(x)在(0,+∞)上也单调递减.
根据f(-4)=0可得F(-4)=0,从而函数图象如图1所示,根据图象知x f(x)>0的解集为(-∞,-4)∪(0,4).
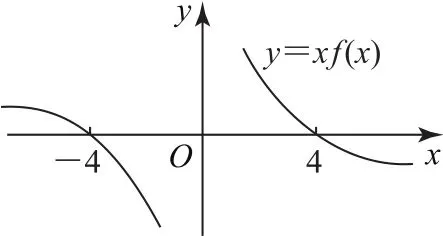
图1
变式f(x)是定义在R上的偶函数,且f(1)=0,当x<0时,有xf′(x)-f(x)>0恒成立,则不等式f(x)>0的解集为________.
解析
2 构造f(x)与e x的关系
由于(ex)′=ex,当给出的不等式中出现f(x)±f′(x)型,我们首先考虑f(x)与ex的关系,和的形式优先考虑构造F(x)=f(x)·ex,差的形式优先考虑构造.
例2已知f(x)是定义在R上的函数,导函数f′(x)满足f′(x)<f(x)对于x∈R恒成立,则有( ).
A.f(2)>e2f(0),f(2 020)>e2020f(0)
B.f(2)<e2f(0),f(2 020)>e2020f(0)
C.f(2)>e2f(0),f(2 020)<e2020f(0)
D.f(2)<e2f(0),f(2 020)<e2020f(0)
解析
变式已知定义在R上的偶函数f(x)的导函数为f′(x),满足f(0)=e2且f(x)>f′(-x),则关于x的不等式的解集为( ).
A.(-∞,-2) B.(-2,+∞)
C.(-∞,0) D.(0,+∞)
解析
根据原函数是偶函数可知f′(-x)为奇函数,又f′(-x)-f(x)<0,故构造函数F(x)=f(x)ex,其在R上单调递增,将f(x+2)>转化为F(x+2)>F(0),再根据其单调性可得x+2>0,从而B选项正确.
3 构造f(x)与sin x,cos x的关系
类比前两类,若题中出现三角函数,就需要构造f(x)与sinx,cosx结合的函数,具体如下:
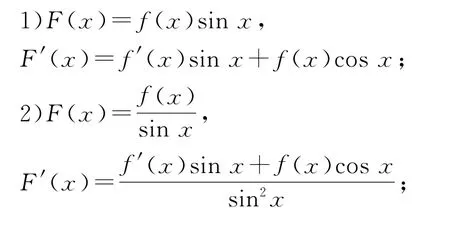
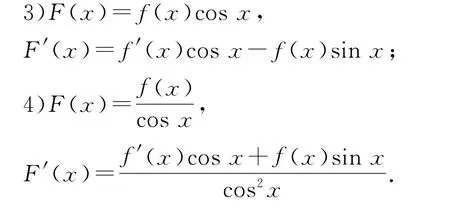
例3已知函数y=f(x)对于任意满足f′(x)cosx+f(x)sinx>0(其中f′(x)是f(x)的导函数),则下列不等式不成立的是( ).
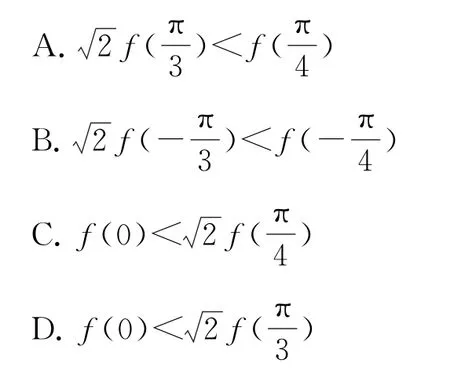
解析
变式已知且αsinα-βsinβ>0,则下列结论正确的是( ).
A.α>βB.α2>β2
C.α<βD.α+β>0
解析
构造f(x)=xsinx,则f′(x)=sinx+时,导函数f′(x)≥0,f(x)单调递增时,f′(x)<0,f(x)单调递减.又因为f(x)为偶函数,根据单调性可知选B.
以上是构造函数在解决与不等式有关的小题中的应用,在求解时,根据问题的条件或目标,构造出一种新的函数关系,在新函数下转化并利用函数的有关性质解决原问题,这是一种行之有效的解题手段.构造函数法解题具有较大的灵活性和技巧性.根据要解决的问题,灵活构造转化,有的放矢,从而使问题迎刃而解.
