解综合性三角函数问题的技巧与方法

◇ 江苏 顾建华

众所周知,解三角函数问题是高考的一个重要内容,在选择题、填空题以及解答题中均有涉及,难度适中,这样的题目一般是不能丢分的.因此,掌握好解题方法非常关键.本文主要介绍高考数学中的解三角函数问题的方法技巧.

1 了解一些三角函数重要的关系

1)同角三角函数的基本关系

a)平方关系:sin2α＋cos2α＝1;

c)倒数关系:tanαcotα＝1.

2)诱导公式

a)设α为任意角,k∈Z,

3)和差公式

注:公式的逆用或者变形.

4)二倍角的正弦、余弦和正切公式

从二倍角的余弦公式里面可以得出降幂公式,即

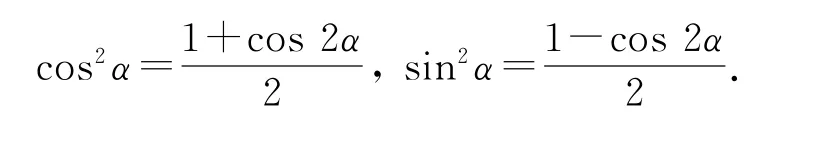
5)辅助角公式

6)半角公式(可由降幂公式推导出)

金融工具的有效性与金融服务的完善必须依托国家的政策为导向，创新投融资平台，建立全体系与全产业的金融服务机制，通过重点项目拓宽现有的投融资渠道，准确发挥金融在贵阳城镇化建设过程中的积极作用。

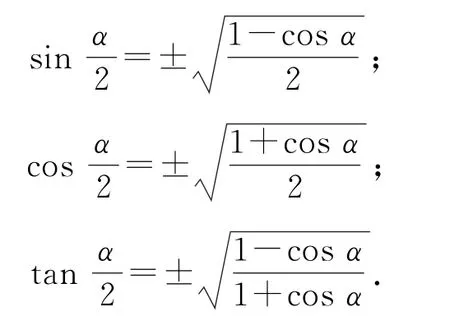
2 例题分析

例1已知tanα＝3,求的值.

解析

点评

利用同角三角函数的基本关系灵活转化,把未知变成与已知条件有关,找到突破点.

例2已知求sinαcosα的值.

解析

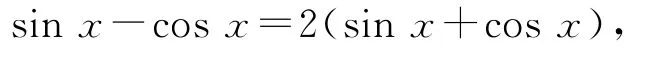
化简可得sinx＝－3cos x.又因为sin2α＋cos2α＝1,可联立方程组

方法2因为所以

则1－2sinαcosα＝4＋8sinαcosα,所以有

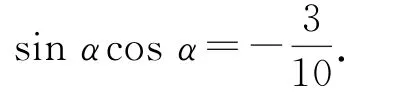
点评

三角函数恒等变形的基本策略有常值代换特别是用“1”代换,如sin2α＋cos2α＝1)、项的分拆与角的配凑、降次与升次、化弦法、引用辅助角公式等.

例3在△ABC中

(1)求sinA的值;

(2)设△ABC的面积求BC的长.

解析

(2)由三角形面积计算公式,得

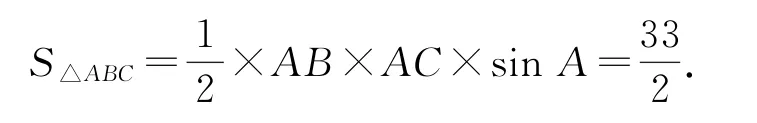
点评

解答高考题中三角函数应用题的策略:首先,观察角以及运算关系间的差异;其次,运用相关公式,找出差异之间的内在联系;最后,选择恰当的公式,促成差异的转化.

三角恒等变形,是三角知识的综合应用,虽然题目类型多样,变化复杂,但处理这类问题其实很简单,我们只需要把三角函数的项数尽可能变少,类型尽可能减少,角尽可能变小,次数尽可能变低,分母尽可能不含三角式、不带根号,能求出值的求出值.然后,我们要注意不同角之间的关系,尽量异名化同名,异角化同角.