物性参数对液晶偏振光栅特性的影响

陈雨诺， 罗炜程， 鄢宏杰， 陈鹭剑*

(1. 厦门大学 电子科学与技术学院，福建 厦门 361005；2. 厦门城市职业学院，福建 厦门361008)

1 引 言

在过去的10年中，几何相位，也称为PB相位(Pancharatnam-Berry phase)方面的研究取得了令人瞩目的进展[1]，与由光程差造成的动态相位变化不同，几何相位变化源于光的自旋-轨道相互作用[2](Spin-orbit interaction，SOI)，描述的是当光通过各向异性介质时，相位变化和偏振态变化之间的关系。由于光波的几何相位仅取决于其通过某一各向异性介质时的几何路径及偏振态[3]，这就使得所选用的介质无需具有很大的尺寸来提供相位积累，且对制作过程中的瑕疵具有较好的鲁棒性[4]。由于以上特点，几何相位调制为光学器件的小型化、集成化提供了更多的可能性。

液晶(Liquid crystal)作为一种可动态取向、电控技术成熟且在可见光波段透过率较高[5]的各向异性材料，是制备几何相位调制器件的理想选择。目前，基于液晶的光电器件已经得到了非常广泛的应用，如空间光调制器[6]、光开光[7-8]、偏振控制器[9]等，从本质上来说，都是利用液晶分子的上述特性，通过外场进行调控，改变光波的相位，从而实现对光强、偏振态等光学特性的调制。

液晶偏振光栅(LC polarization grating，LCPG)就是一种典型的可以实现几何相位调制的液晶器件。2004年，美国布朗大学的Crawford等人首次利用两束正交圆偏振光的全息曝光得到液晶偏振光栅[10]。但由于其使用的是单玻璃基底和取向完全固定的聚合物液晶，所以无法通过电压进行调制，这种无源的液晶偏振光栅，被称为被动式液晶偏振光栅[11]。与之对应的是本文涉及的主动式液晶偏振光栅，其基本特征为：两块平板玻璃之间限定具有介电各向异性和光学各向异性的向列相液晶，并通过特定取向使液晶分子沿基板平面进行周期性排布，在每个周期内液晶分子的指向矢旋转了180°的光栅[11]。与被动式液晶偏振光栅不同，该光栅可以通过电压进行调制，对于本文接下来提到的液晶偏振光栅，若无特殊说明，统一指主动式液晶偏振光栅。

目前，液晶偏振光栅已经在高精度高偏转的光束偏转系统[12-13]中展示出了广泛的应用前景，如激光扫描系统、红外凝视系统、偏振成像系统[5]、激光雷达系统[14]等，它也因此被称为第四代光学元件。但是，国内外对其的研究至今还比较有限，仍有一些技术难点未被攻克，以至于至今鲜有成熟的采用液晶偏振光栅为核心器件的光学系统。

自20世纪80年代偏振光栅的概念首次被提出以来，液晶偏振光栅在衍射效率[15]、工作波段[16-19]等方面都有了长足的技术进展。2007年，Komanduri等人基于液晶的弹性连续体理论构建了液晶偏振光栅的弹性连续体模型，通过该模型，对液晶偏振光栅的部分结构、电光特性参数得以被计算并分析，这些分析的结果对于其制备过程是有很大的指导意义的[20]。该工作主要关注液晶偏振光栅周期对两个基本的特性——临界盒厚和阈值电压的直接或间接的影响。液晶偏振光栅的结构特性很大程度上依赖于储存液晶光栅的液晶盒尺寸，当液晶盒厚超过对应临界盒厚时，所制备的液晶偏振光栅中会出现液晶分子的排列缺陷，即在无外加电场的情况下，液晶分子指向矢与液晶盒上下表面不严格平行，这对液晶偏振光栅的衍射效率和偏振调制特性有着严重的影响。阈值电压也称为液晶偏振光栅的弗雷德里克兹转变条件，当给液晶偏振光栅一个小于阈值电压的外加电压时，液晶盒内的液晶分子排列几乎不受到该外加电场的影响，而当外加电压大于阈值电压时，就可以通过它来控制液晶分子的倾角。鉴于对液晶偏振光栅的各级能量分布、衍射效率、偏振态等的理论研究和实验验证已有不少[5]，实验成果也已经较为完善，且这些实验都需要建立在液晶盒厚小于临界盒厚、外加电压大于阈值电压的基础上，所以本文以可以通过偏振或外加电压来控制液晶偏振光栅衍射光的先决条件：临界盒厚和阈值电压为切入点开展分析和研究。

本文首先介绍液晶偏振光栅的弹性连续体模型的构建，然后应用该模型分别在强锚定条件和弱锚定条件两种情况下，针对具有不同盒厚与光栅周期的液晶偏振光栅进行理论计算和分析，讨论液晶物性参数对关键特性参数即临界盒厚和阈值电压的影响规律，并进行总结和展望。

2 模型介绍

2.1 液晶偏振光栅的弹性连续体模型

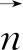
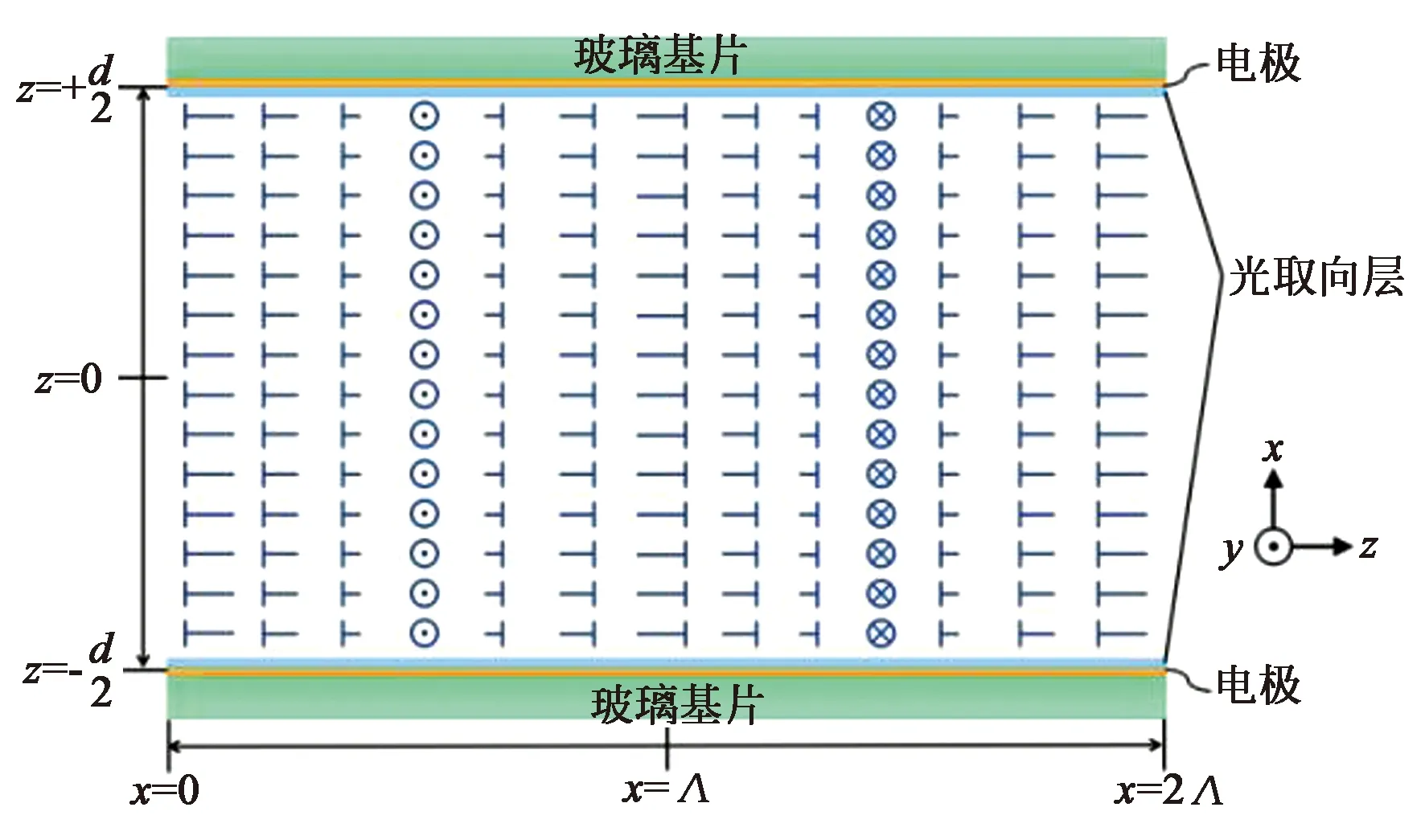
图1 液晶偏振光栅结构示意图

，

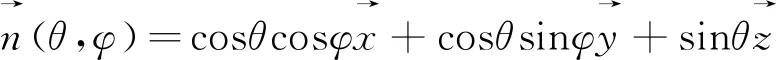
(1)

其中，θ和φ分别为空间坐标系中的倾斜角、方位角。由于液晶盒空间边界条件的限制，θ和φ都是关于y坐标独立的[5]，因此研究中大多使用如图1的剖面来表征液晶偏振光栅的基本结构。

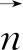
其中:K1、K2、K3分别为所使用液晶材料的展曲弹性常数、扭曲弹性常数和弯曲弹性常数。当给液晶偏振光栅外加一个电场时，液晶盒内的电场能量密度可表示为：

，

(3)

其中:ε0为真空介电常数，Δε为所使用液晶材料的介电各向异性。

当给液晶偏振光栅外加一个大于阈值电压Vth的电压V，其液晶分子将会发生偏转，与玻璃基片间形成一定的倾角。如图2所示，在给定空间边界条件限制和外加电场时，可以通过变分法计算总自由能密度最小时的液晶分子指向矢分布[24]，进而进行该平衡态下其他电光特性参数的计算。

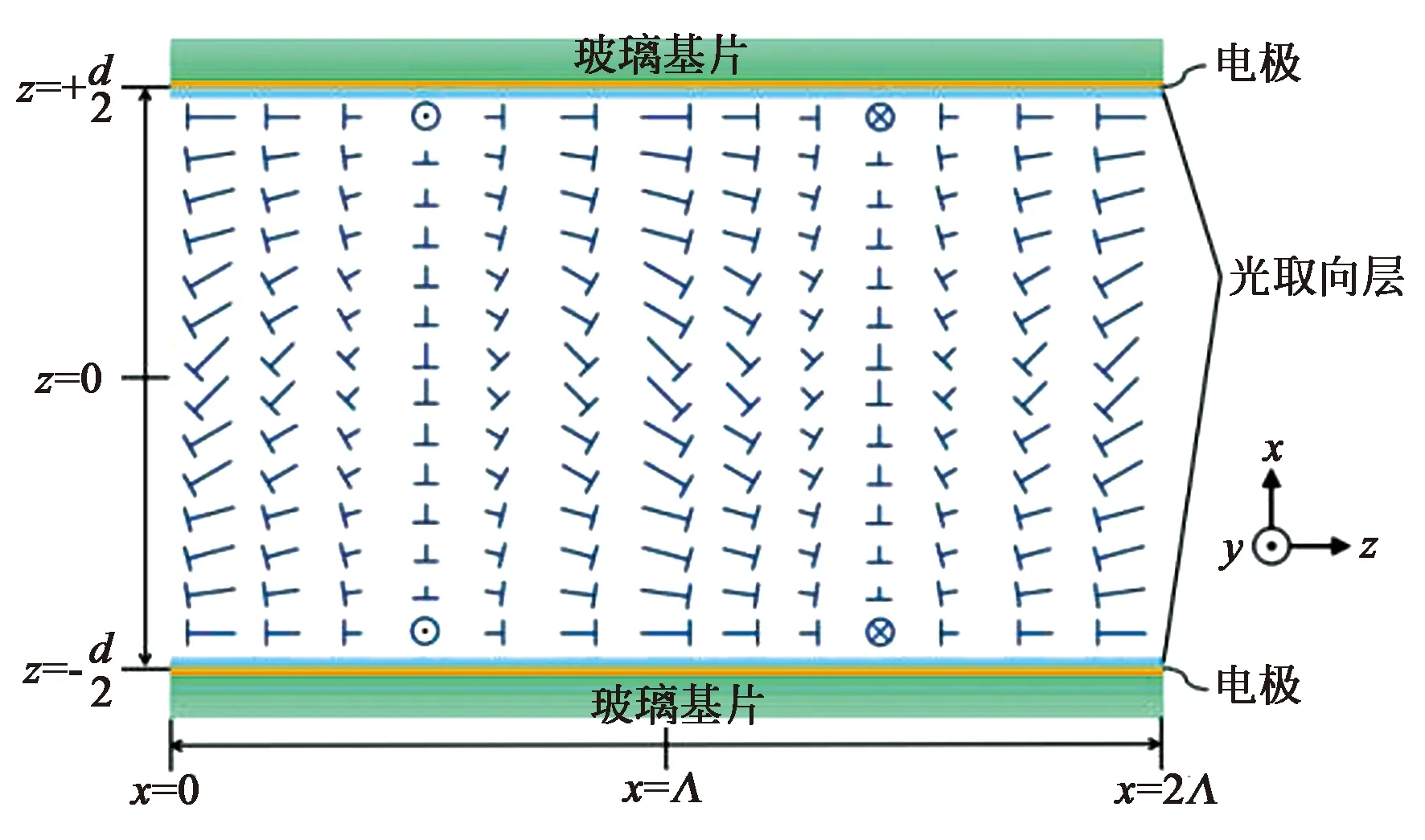
图2 V>Vth时液晶偏振光栅结构示意图

求和得到液晶偏振光栅的总自由能密度为：

，

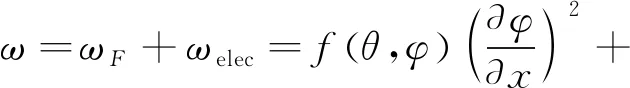
(4)

其中:

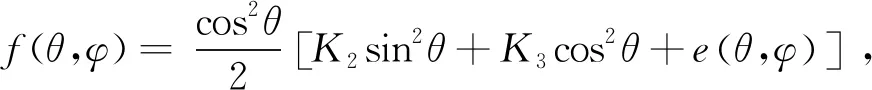
引入一个取值为[-1, 1]的常数α来替代耦合项f(θ,φ)，最终可以得到液晶分子指向矢倾斜角θ、空间坐标z、液晶盒厚度d以及外加电场场强E之间的关系[23]：

，

(5)

其中:

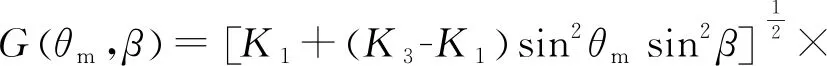
以式(5)为基础推导出液晶偏振光栅一系列特性参数的表达式，并且可以分析图1与图2之间的弗雷德里克兹转变过程，特别地，在模型中也使用了α=0.4这一经验取值[20]。

2.2 模型中的锚定条件

由于液晶的流动性，所以一般应用时都将液晶装在液晶盒内，这就使得我们不得不考虑液晶和包裹着它的液晶盒内表面间的相互作用，即界面作用。在界面作用中，锚定能(Anchoring energy)的大小决定了锚定条件的强弱，强锚定条件描述的是锚定能足够大时液晶分子指向矢在表面处被固定且难以被改变的情况，与之相对的，液晶分子指向矢在表面处容易被改变的情况，被称为弱锚定条件[25-26]。

光取向技术是制备基于液晶材料的几何相位元件所采用的最主要的取向技术之一[27]，自Ichimura等[28]1988年首次提出光取向技术以来，该技术就得到了广泛研究和发展[29-31]。2002年，Chigrinov等人[32]开发出了一种基于磺酸基偶氮染料及其衍生物的光控取向材料SD1，不仅很好地解决了偶氮类材枓的光、热稳定性问题，改良了偶氮类材枓的电压保持率，而且使得光取向技术可以提供与摩擦取向技术相比拟的锚定能(>10-4J/m2)[33]。

此外，可以通过改变液晶原材料的平均分子长度[34]、调整曝光方法[35]、改变光取向材料[36]等方法来改变锚定能。光取向的强锚定条件在目前的技术水平下已经是稳定可靠的，但受限于实验条件，有时不得不使用仅能提供弱锚定条件的光取向材料[37]。弱锚定条件下，液晶盒表面处的液晶分子指向矢更容易被改变，对弱锚定条件进行研究有助于解决液晶偏振光栅制备过程中产生瑕疵的问题[38-40]。

2.1节中的推导过程是基于光取向的强锚定条件，在此基础上，Komanduri也对模型在弱锚定条件下进行了修正[20]，在体系的总能量密度算式中加入液晶盒中的表面锚定能量密度项[41]：

，

(6)

其中:Wp和Wa分别是液晶盒表面处液晶分子指向矢倾斜角θ和方位角φ方向上的锚定能。并引入关于液晶材料的单一弹性常数近似，即可获得适用于弱锚定条件下的模型。使用该模型可以对强、弱两种锚定条件下液晶偏振光栅的特性参数进行计算与分析。

2.3 输入模型的物性参数

从式(5)可以看出，影响液晶偏振光栅中液晶分子指向矢倾斜角θ、空间坐标z、液晶盒厚度d以及外加电场场强E之间关系的液晶材料物性参数有：液晶的介电各向异性Δε和分别对应展曲、扭曲、弯曲的弹性常数K1、K2、K3。

液晶分子在多种性质上都呈现出各向异性，而液晶材料在电场中的大部分物理学参数都是由介电各向异性所决定的[42-43]。对于在光学波段常用的正性液晶材料，其介电各向异性的取值范围一般为[5, 100][44]。通过掺杂等方法可以对液晶的介电各向异性进行调整。例如，2004年，Thisayukta等人提出的在向列相液晶中加入银纳米粒子的方法，可以实现对向列相液晶电光特性的改变[45]。

弹性常数Ki(i=1,2,3)是一种用来描述液晶分子弹性形变的物理量。通常，Ki的取值应在pN量级，且通过实验已经得到了一般液晶的3个弹性常数之间比值的大致范围[46]为：

.

(7)

在实验中，可以通过改变所使用液晶分子的尺寸、刚性或通过掺杂来实现K2/K1和K3/K1值的变化[47]。例如，增大液晶分子的长度或提高液晶分子的刚性即可有效提高K3/K1值[46]。

尽管在液晶体系中，Δε和K1、K2、K3之间存在着一定的相互影响，但在大部分对向列相液晶物性特征的研究中，这些参数都被分开来讨论[48]。因此，在本研究中也将对这两个输入的物性参数分别独立地在取值范围内取值。

3 强锚定条件下的计算

为了获得更高的计算效率和精度，本节把模型移植到MATLAB中进行计算，并做了部分改动和优化。考察一种常见的向列相液晶MLC-6080，其介电各向异性为Δε=+7.2，弹性常数[K1,K2,K3]=[14.4, 7.1, 19.1] pN，且α取值为0.4保持不变，由于弹性常数在本节的计算中主要以K2/K1和K3/K1的形式出现，所以固定K1的值不变，通过K2和K3值的改变来实现上述两个比值的变化。

3.1 临界盒厚

强锚定条件下，根据上述构建的模型，在无外加电场且不考虑液晶分子指向矢存在预倾角时，在液晶盒中心即空间坐标z=0处应有θm=0，将此条件代入式(5)得到：

，

(8)

简化后得到液晶偏振光栅的临界盒厚dc的表达式：

，

(9)

由此可见，液晶偏振光栅的临界盒厚是一个由光栅周期Λ和液晶材料弹性常数比值K2/K1、K3/K1共同决定的参数。

在一组固定光栅周期Λ下，研究临界盒厚dc与液晶材料物性参数K2/K1、K3/K1的关系。由于在越小的光栅周期下，临界盒厚的确定就越有意义，因此本文在接下来的研究中结合液晶偏振光栅常见的设计光栅周期，在一个较小的微米量级对其进行取值。图3和图4分别展示了Λ分别为2，5，10，20 μm时dc与K2/K1、K3/K1的关系，其中红色曲线反映的是dc的变化规律，为了直观体现其与光栅周期的对比，用黑色曲线在纵坐标上标注出了Λ值。

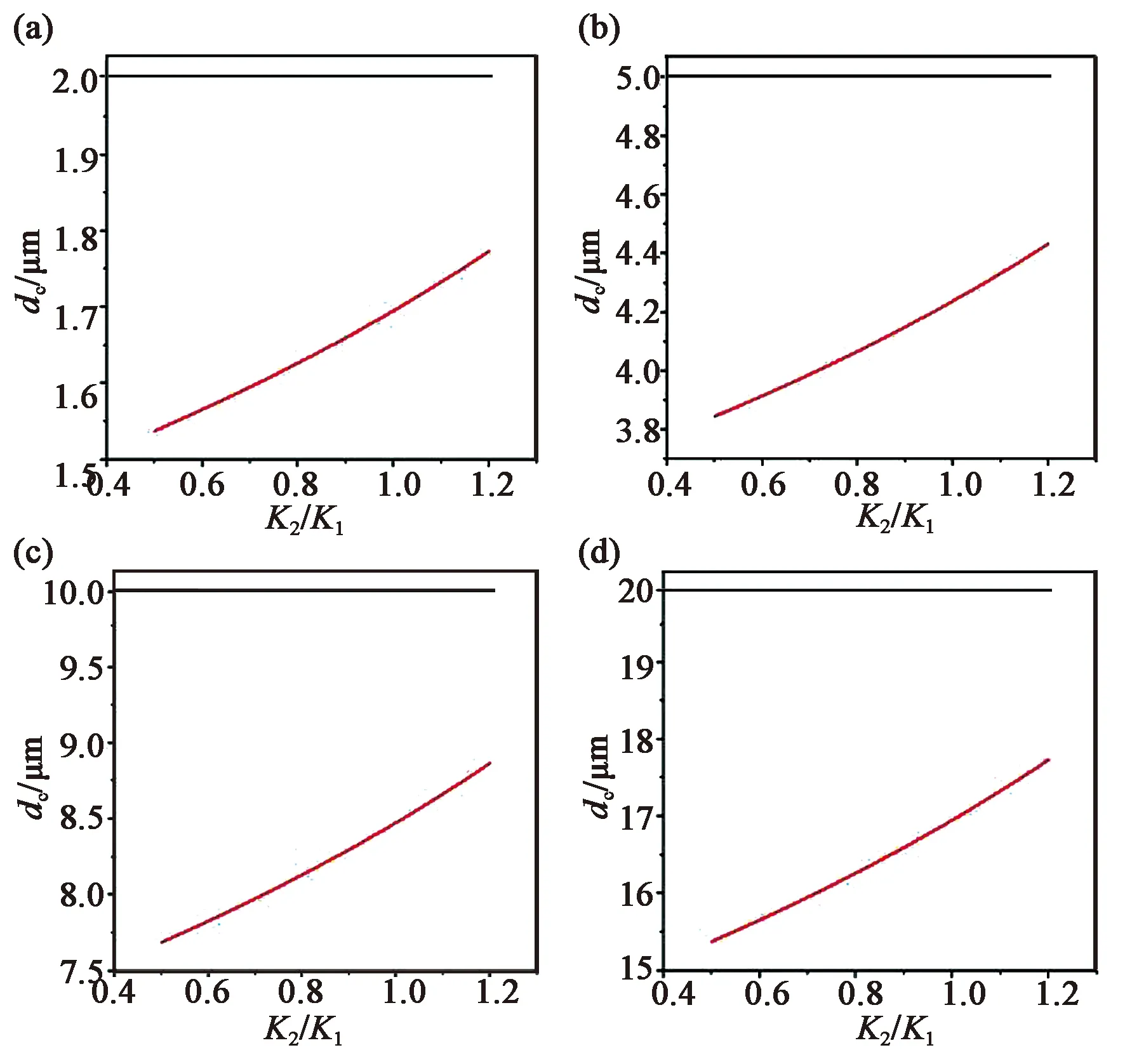
图3 Λ不同取值时dc与K2/K1的关系。(a) Λ=2 μm；(b) Λ=5 μm；(c) Λ=10 μm；(d) Λ=20 μm。

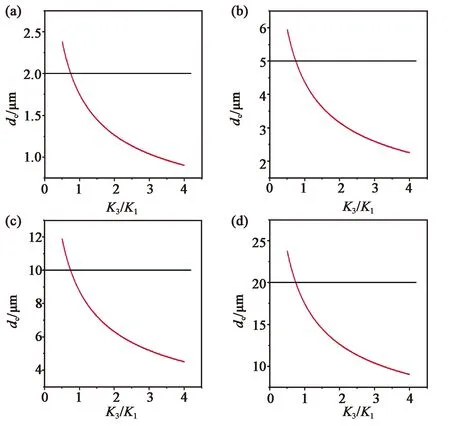
图4 Λ不同取值时dc与K3/K1的关系。(a) Λ=2 μm；(b)Λ=5 μm；(c) Λ=10 μm；(d) Λ=20 μm。

可以看出，图中的黑色曲线和红色曲线在纵坐标取值上是相当接近的，且表现出与K2/K1、K3/K1不同的相关性，这是由这两个参数在式(9)中所处的位置决定的，总结如下：在强锚定条件下，液晶偏振光栅的临界盒厚dc分别表现出与K2/K1值正相关，与K3/K1值负相关，且dc的值总是与Λ相近的。

理论上，当液晶处在液晶盒中时，液晶分子同时存在展曲、扭曲和弯曲3种形变，扭曲弹性常数K2描述的就是液晶材料形成扭曲结构难易程度的一个参数，较低的K2值说明该液晶材料更容易产生扭曲结构，对于使用了K2值较大的液晶材料的液晶偏振光栅，当液晶盒厚度d改变时，扭曲形变将会更容易克服另外两种形变的约束，造成液晶分子取向不再平行于液晶盒上下表面，容易引起液晶分子排布上的缺陷，进而对液晶偏振光栅的性能产生负面影响，这与本研究分析得出的结果是一致的。

3.2 阈值电压

强锚定条件下，当液晶盒厚度d小于液晶偏振光栅临界盒厚dc时，对其施加一个电场使得液晶盒两端电压恰好为阈值电压，此时在液晶盒中心即空间坐标z=0处应有θm=0，将此条件代入式(5)得到：

，

(10)

将式(9)代入化简即可得到阈值电压Vth的表达式：

，

(11)

显然，液晶偏振光栅的阈值电压是一个由光栅周期Λ、弹性常数K1、K2、K3、介电各向异性Δε共同决定的参数，由于Vth的计算同时涉及液晶盒厚度和设计光栅周期的选取，在液晶偏振光栅的设计中，这两个参数都十分重要，为了同时将二者都纳入变量考虑，结合它们在式(11)中的位置，本文将固定一组液晶盒厚度与光栅周期的比值d/Λ来分别研究Vth与K2/K1、K3/K1以及Δε的关系，由式(11)可知，这一比值的最大值只能为1，否则会产生小于0的阈值电压。

图5和图6分别展示了d/Λ分别为0.2，0.4，0.6，0.8，1，时Vth与K2/K1、K3/K1的关系。

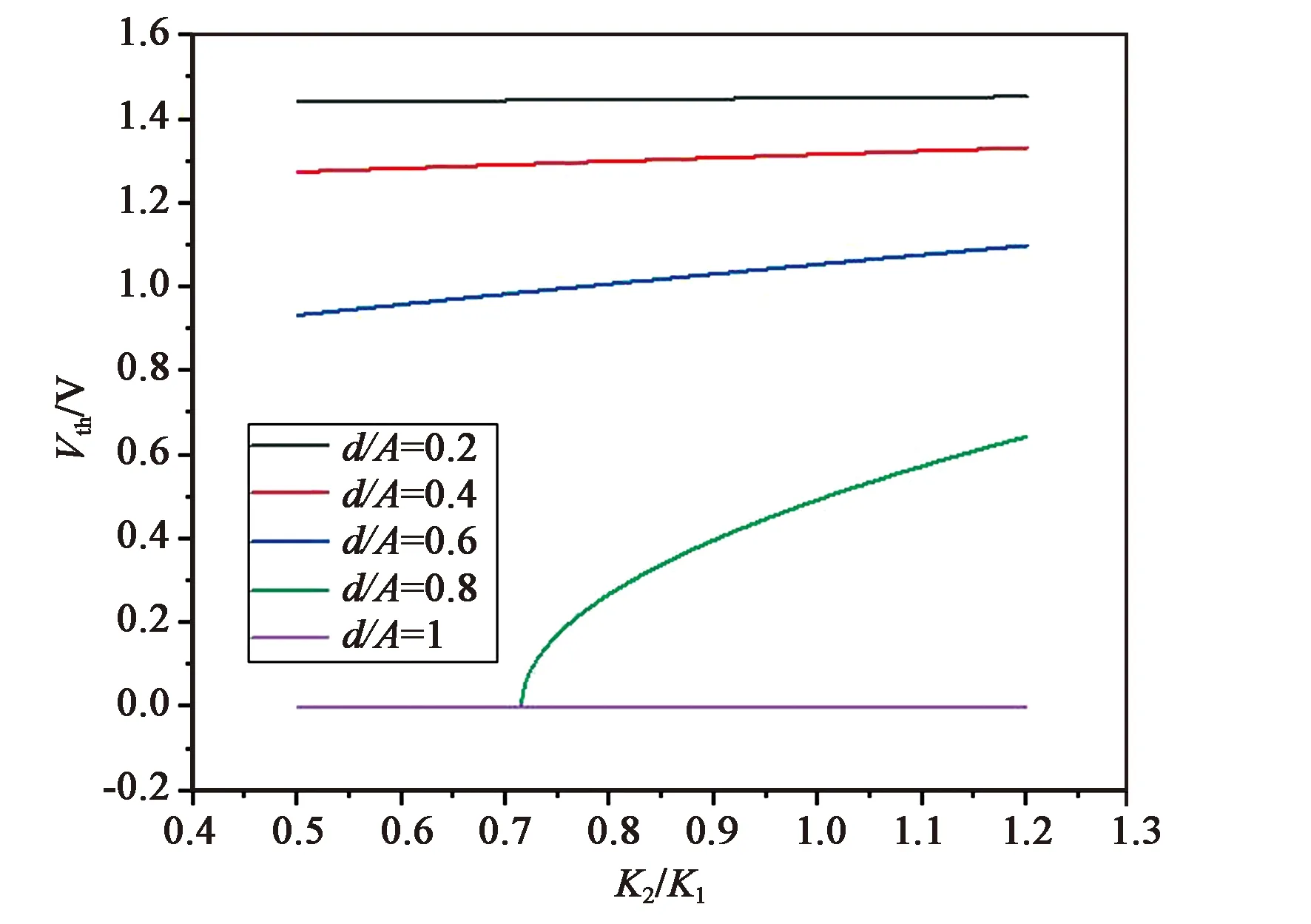
图5 d/Λ不同取值时Vth与K2/K1的关系

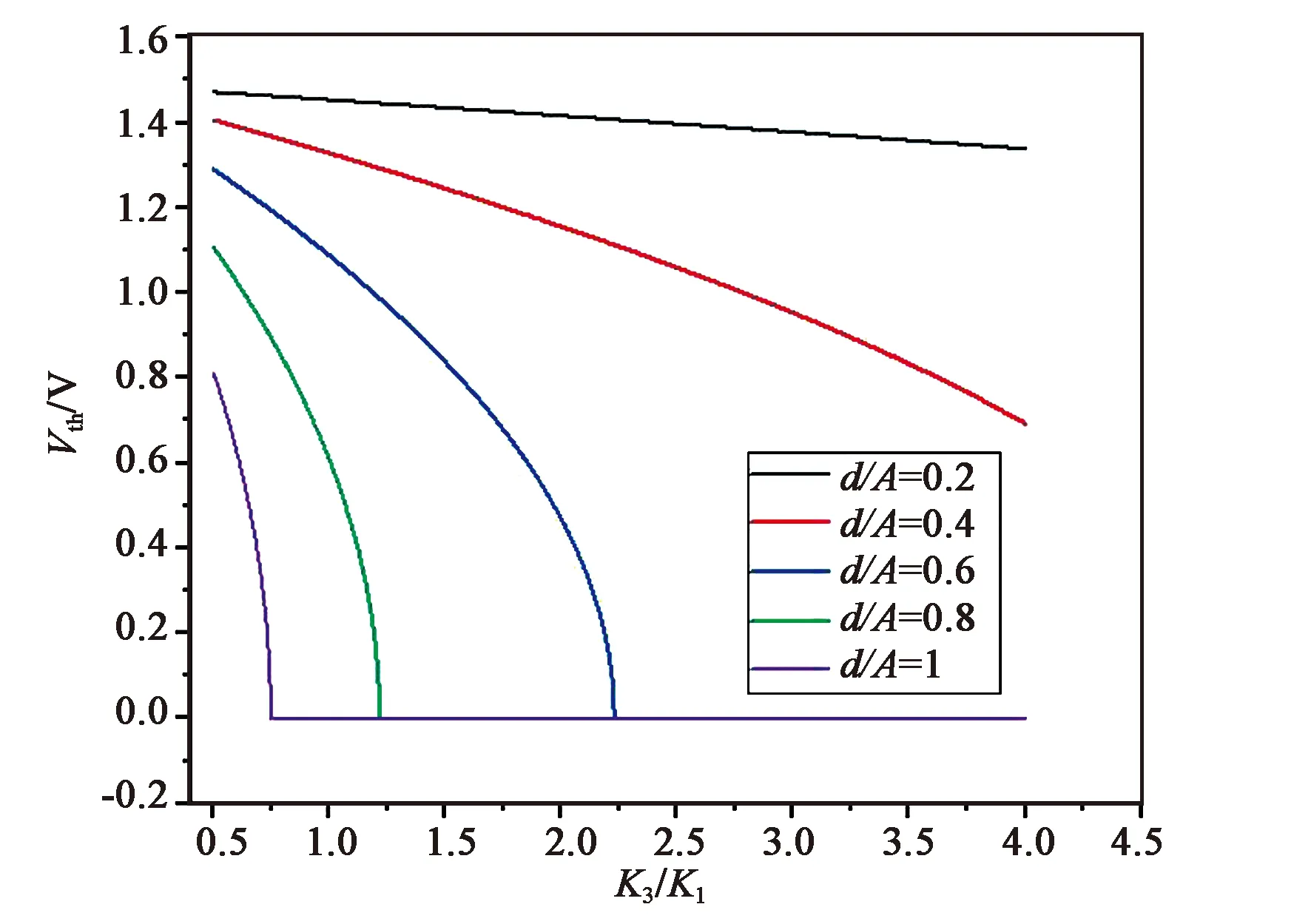
图6 d/Λ不同取值时Vth与K3/K1的关系

可以看出，在强锚定条件下，液晶偏振光栅的阈值电压Vth分别表现出与K2/K1正相关、与K3/K1负相关，这与dc在Vth的表达式中所处的位置相符，同时，随着d/Λ越来越接近1，这种相关性逐渐变强，Vth的值也越来越趋于0，这与随着液晶盒厚度增大，液晶分子越发地容易产生相对于液晶盒上下表面的倾斜角是相符的。

图7展示了d/Λ为0.2，0.4，0.6，0.8，1时，Vth与Δε的关系。其中，d/Λ为0.8和1的曲线几乎在0处重合，可以看出，在强锚定条件下，液晶偏振光栅的阈值电压Vth表现出与Δε的负相关性，且使得Vth有一个较大的可调范围。同样，随着液晶d/Λ的增大，Vth的值也越来越趋于0。

图7 d/Λ不同取值时Vth与Δε的关系

4 弱锚定条件下的计算

前文已经提到，在弱锚定条件下需要引入液晶材料的单一弹性常数近似，即将所使用液晶材料的展曲弹性常数K1、扭曲弹性常数K2和弯曲弹性常数K3视为相等，在本节的计算中，同样考察MLC-6080，当改变其中的某一项物性参数时，以K=K1作为单一弹性常数的值，且α取值为0.4保持不变。

4.1 临界盒厚

，

(12)

显然，液晶偏振光栅在弱锚定条件下的临界盒厚是一个由光栅周期Λ、弹性常数K和表面处液晶分子指向矢倾斜角上的锚定能Wp共同决定的参数。接下来，本文将固定一组光栅周期来研究此时临界盒厚与弹性常数的关系，这里令Wp=10-5J/m2，这是一个弱锚定条件下的锚定能(<10-4J/m2)。

图8展示了Λ分别为2，5，10，20 μm时，d′c与K的关系，这里对K按照常见弹性常数值取值[5, 50] pN，图中红色曲线体现的是d′c的变化，并用用黑色曲线在纵坐标上标注出了Λ值。

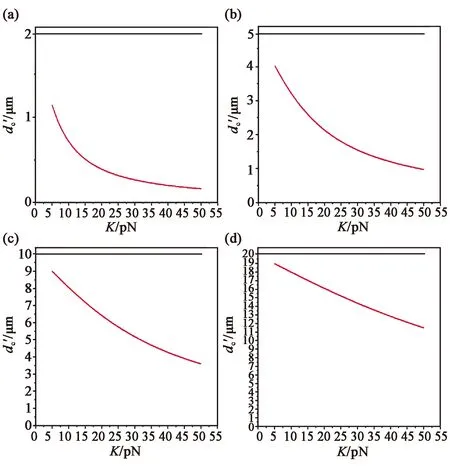
图8 Λ不同取值时d′c与K的关系。(a) Λ=2 μm；(b) Λ=5 μm；(c) Λ=10 μm；(d) Λ=20 μm。

可以看出，在弱锚定条件下，液晶偏振光栅的临界盒厚d′c在与光栅周期相近的基础上表现出与K的负相关性，且在相同条件下，临界盒厚要比强锚定时的小。

4.2 阈值电压

弱锚定条件下，把液晶偏振光栅的阈值电压记作Vth′，使用与3.1.1小节中类似的化简过程即可得到其表达式：

，

(13)

其中：

因为β0的取值与强锚定条件下的阈值电压Vth有关，需要将以上两式以强锚定为初始条件迭代求解才可以得到在特定Wp时的阈值电压。

显然，Vth′是一个由Λ、K和Wp共同决定的参数，图9展示了d/Λ分别为0.2，0.4，0.6，0.8，1时，Vth′与K的关系，这里同样令Wp=10-5J/m2。其中d/Λ为0.8和1的曲线几乎在0处重合，可以看出，在弱锚定条件下，液晶偏振光栅的阈值电压Vth′仅在d/Λ较大时表现出与K有较强的负相关性，同时，随着d/Λ的增大，Vth′的值也越来越趋于0，这与强锚定时的情况是相似的。

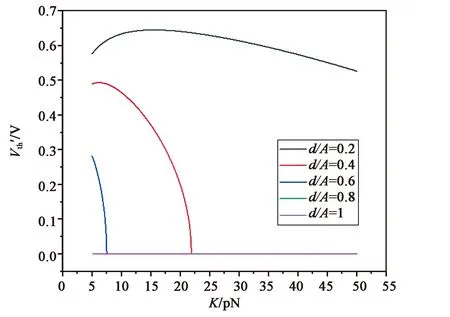
图9 d/Λ不同取值时Vth′与K的关系

图10展示了d/Λ分别为0.2，0.4，0.6，0.8，1时，Vth′与Δε的关系。其中，d/Λ为0.6、0.8和1的曲线几乎完全重合，可以看出，在弱锚定条件下，Vth′表现出与Δε负相关，与强锚定时的趋势是相似的。同样，随着液晶盒厚度、光栅周期比值的增大，Vth′的值也越来越趋于0。总体来看，在相同条件下无论改变任意一个物性参数，弱锚定时的阈值电压都要比强锚定时的要小。

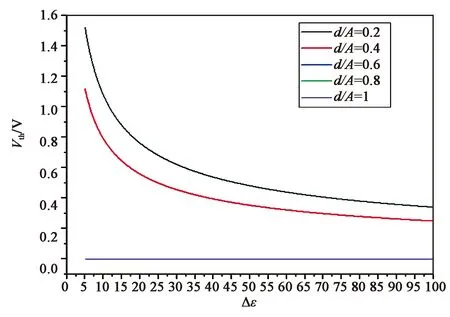
图10 d/Λ不同取值时Vth′与Δε的关系

4.3 弱锚定条件与强锚定条件的对比

将4.1节和4.2节的结果与强锚定条件下的结果进行对比可见，液晶偏振光栅的临界盒厚和阈值电压在强、弱锚定下受到物性参数的影响存在相似性，在这一小节，以Wp为自变量，研究锚定能增大的过程中，强、弱两种锚定条件下推导出的表达式的关系。

保持其他条件不变，固定液晶盒厚度d=2 μm，使强锚定下的液晶偏振光栅临界盒厚和阈值电压为定值，而弱锚定下的液晶偏振光栅临界盒厚和阈值电压为Wp的函数，随着Wp取值从一个几乎无法提供锚定作用的锚定能(10-7J/m2)到可以提供强锚定作用的锚定能(10-3J/m2)，对于d/Λ分别为0.2，0.4，0.6，0.8，1时，d′c/dc关于Wp的规律如图11所示。

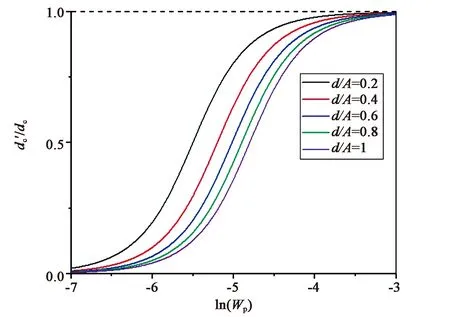
图11 d/Λ不同取值时与Wp的关系

由于当d/Λ为1时Vth=0，Vth′/Vth没有意义，所以对于d/Λ分别为0.2，0.4，0.6，0.8，做出Vth′/Vth关于Wp的图像如图12所示。可以看出，随着Wp的增加，d′c/dc和Vth′/Vth逐渐增大，且d/Λ越小，增大速度越快，并在锚定强度接近强锚定条件后都趋于1，即当锚定能足够大时，这两个表达式与强锚定条件下的表达式是接近等价的，该结论进一步证明了模型在两种锚定条件下的一致性。

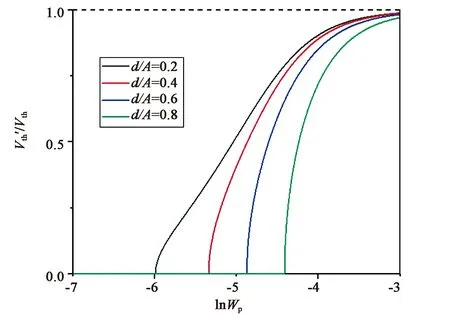
图12 d/Λ不同取值时Vth′/Vth与Wp的关系

5 结 论

本研究借助Komanduri所构建的液晶偏振光栅弹性连续体模型[20]，对强锚定、弱锚定两种条件具有不同盒厚与光栅周期的液晶偏振光栅的两个基础性能，即临界盒厚和阈值电压与液晶材料物性参数如弹性常数、介电常数等的关系进行分析和对比。以下是对上文分析结果的一个小结，希望对液晶偏振光栅制备过程中的液晶物性参数选择给出一定的理论参考依据。

临界盒厚：在制备液晶偏振光栅时，尤其是小周期的液晶偏振光栅，一般期望其有足够大的临界盒厚，若使用的是可以提供强锚定条件的光取向材料，则选取值K2/K1较大、K3/K1值较小的液晶材料，可以在相同条件下获得更大临界盒厚；若使用的是仅能提供弱锚定条件的光取向材料，则应选取K较小的液晶材料可以在相同条件下获得更大临界盒厚；在其他条件都相同的情况下，使用能提供强锚定条件的光取向材料可以获得更大的临界盒厚。

阈值电压：与临界盒厚不同，不同的应用场景对阈值电压有不同的要求，若使用的是可以提供强锚定条件的光取向材料，当需要液晶偏振光栅有一个较大的阈值电压时，可以考虑使用K2/K1值较大，K3/K1、Δε值较小的液晶材料，而当需要液晶偏振光栅有一个较小的阈值电压时，可以考虑使用K2/K1值较小，K3/K1、Δε值较大的液晶材料，且当液晶盒厚度与光栅周期比值越接近1，对阈值电压的调整效果越好；若使用的是仅能提供弱锚定条件的光取向材料，当需要液晶偏振光栅有一个较大的阈值电压时，可以考虑使用Δε值较小的液晶材料，而当需要液晶偏振光栅有一个较小的阈值电压时，可以考虑使用Δε值较大的液晶材料，特别是当弱锚定条件下液晶盒厚度、光栅周期比值较大时，阈值电压和K有较强的负相关性。

虽然以上分析解释了液晶偏振光栅的两个基础性能参数与液晶材料物性参数的关系，但是液晶偏振光栅还有许多其他的性能参数尚存在未解决的问题，如光栅响应时间等。在未来的研究中若要对其进行分析，则要将更多的液晶物性参数纳入模型中进行考虑，并对液晶偏振光栅的弹性连续体模型做进一步的优化。