在深度学习中培养学生的高阶思维
2020-12-07陈华忠
陈华忠
高阶思维是学生深度学习的重要标识。教学中,教师要借助深度学习发展学生高阶思维,通过高阶思维活动,促进学生深度学习。在数学教学中,教师可以引导学生深度思考、深度探究和深度交流等,通过深度学习培养学生的高阶思维。
所谓高阶思维,是指学生的思维具有发散性、结构性、主动性、批判性等特质。发展学生的高阶思维,需要学生展开深度学习。同样,学生的深度学习能促进学生高阶思维的发展,高阶思维与深度学习是相辅相成、相互促进的关系。高阶思维能力主要包含创新能力、问题求解能力和批判性思维能力等,是数学思维能力的核心。那么,如何在数学教学中培养学生的高阶思维呢?这是值得教师深入探究与思考的问题。
一、问题驱动,引发高阶思维
教学中,教师要把问题作为思维主线,以问题为驱动,用有价值的问题去影响学生的高阶思维。为此,在教学中,教师应注意设置有价值的问题,引导学生思考、探究、解决问题,从而培养学生的高阶思维。
1.开放性问题。没有现成答案的开放性问题对学生更具有吸引力,更具有挑战性,学生的思维不易受到限制,其思考过程更能锻炼学生的高阶思维。
例如,教学“三角形的内角和”一课,在布置巩固练习时,教师出示这样一道题:“一个等腰三角形有两个角被盖住,露出的是一个42°的角,猜一猜,这个三角形按角分是什么三角形?”这个问题是开放的,学生应思考:露出的角是什么角?有几种可能?当它是顶角时,它是什么三角形?当它是底角时,又是什么三角形?这样的开放题训练,既有利于学生更好地理解和掌握三角形的内角和及三角形的分类知识,又有利于培养学生的创新意识,培养学生的数学思维。
又如,教学“重叠问题”一课,在布置巩固练习时,教师出示这样一道题:甲文具盒有6种文具,乙文具盒有5种文具,问两个文具盒中一共可能有多少种文具?这道题让学生体会到,两个集合之间除了能出现交集之外,也可能没有交集,还可能一个集合完全包含在另一个集合中。简单的素材,多维的应用,蕴含了充分的思考与探索,深化了概念的内涵,扩展了知识的外延,培养了学生的数学思维。
2.层次性问题。设置递进式、层次性问题,有利于学生找到思考问题的切入点和保持思维的连续性,这样的问题对学生有很大的吸引力。学生在分析问题、解决问题过程中训练高阶思维。
例如,教学“小数乘小数”一课时,教师先出示课本情景图,让学生寻找数学信息,提出问题,并列式解答,即2.5×1.3=( ),再出示以下几个问题:
(1)想一想,这道题应怎样计算?(先把因数扩大成整数,然后再把积缩小。)
(2)借助什么计算方法?(借助整数乘小数计算方法。)
(3)今天的计算方法与之前的计算方法有什么异同点?(不同之处在于今天两个因数都要扩大。)
(4)用这种方法还能计算2位小数乘1位小数吗?(可以。)
第一个问题和第二个问题为学生提供了思维的角度和梯度。第三个问题通过知识类比,学生学会分析、比较的方法,学习新知。第四个问题引领学生进行知识拓展,实现思维的阶梯式爬坡。通过层次性问题的思考与探究,把原有知识进行重新构建和发展,学生感受知识的内在联系,从而对小数位数更多的乘法计算产生探究欲望,也提高了解决问题的能力,发展了高阶思维。
3.追究式提问。追问,有效地促进学生深入思考,积极探究,从而培养学生的高阶思维能力。
例如,在教学“3的倍数特征”时,教师先引导学生利用百数表圈画,学生经历猜测、分析、判断、验证等活动后得出:一个数的各个位上数的和是3的倍数,这个数就是3的倍数。但很多学生还是不理解其背后所蕴含的道理,教师适时追问:判断一个数是不是3的倍数,为什么要看各个位上数的和?教师将问题指向本质,引导学生交流讨论,辅以课件直观演示说理,如在判断142是不是3的倍数时,课件呈现142个珠子,142中的“1”表示10个十。1个十,3个3个地分余1(10÷3=3……1),10个十,3个一份共余下1个1(100÷3=33……1),即余1;142中的“4”表示4个十,4个十,3个一份共余4个1,即余4;再加上个位上的2个1。因而,1+4+2可理解为百位、十位、个位上的数字分别除以3后得到的余数总和。经过这样的探索交流、推理,学生不仅记住了这一重要知识点,还能深度理解知识背后蕴含的原理,感受到数学学习不是生硬的,而是有道理的。為此,教师通过追问,引发学生深入思考与探究,使学生真正做到知其然还知其所以然。
4.生成性问题。《义务教育数学课程标准(2011年版)》指出:教学中要合理地利用生成性教学资源,以提高教学的有效性。为此,教学时,教师要善于捕捉学生动态学习中的资源,尤其要巧用学生的错误资源,引导学生在改错、纠错中不断进步,探寻错误根源,促进学生思维发展。
例如,教学“小括号”一课后,在巩固练习时,教师出示这样的一道题:工人每天上午工作4小时,下午工作3小时,平均每小时能做8个零件,请问工人每天可以做多少个零件?
师:根据提供的信息和问题,你会列式吗?要列综合算式哦。
[学生做题,教师巡视,巡视的过程中有意收集错解,展示学生的作品:8×4+3=8×7=56(个)]
师:你们有什么想说的吗?
生1:运算顺序错了,应该先算乘法再算加法。
师:他为什么先算加法再算乘法呢?
生2:因为工人一天工作了7小时,要先算4加3,我觉得要加小括号。
师:你真棒!添上小括号,就变成了8×(4+3)=8×7=56(个)。你们还有什么想说的吗?
生3:小括号真了不起,帮助我们解决了问题。
生4:现在变成先算一天一共工作了7小时,再算8乘7的积。
这样,教师充分利用错误资源,让学生亲身经历小括号产生的过程,理解小括号的作用,也培养了学生的思维能力。
二、提供思辨,激发高阶思维
认知冲突可以调动学生学习动机,让学生积极参与思维活动,是高阶思维能力形成的重要途径。为此,教学中,教师要抓住学生认知冲突,提供思考机会,引导学生进行思辨,激发学生高阶思维,培养学生学习能力。
1.营造认知冲突,让学生进行思辨,激发高阶思维。在数学教学中,教师要制造认知冲突,启发学生独立思考、自主探究、合作交流,在交流中不断产生思维碰撞,从而培养学生的思维能力。
例如,教师在教学“中括号”一课后,学生明白了要改变运算顺序,不但要用到小括号,有时还要用到中括号。巩固练习环节教师出示3道题:90÷10+5×2,90÷(10+5)×2,90÷[(10+5)×2],让学生说运算顺序,再算得数。学生算完之后说说自己的想法,有的学生发现数字和运算符号没有改变,第一题没有括号,第二题有小括号,第三题既有小括号又有中括号。有的学生发现3道题的答案不一样,有的学生受到启发,发现小括号和中括号的存在,改变了运算顺序,其计算结果也不一样。这样,在分析比较中启迪学生的思维,有利于培养学生的高阶思维。
2.制造认知冲突,让学生进行分析评判,发展高阶思维。在数学教学中,教师要引导学生在认知冲突中思考问题,促使学生积极探究有意义的事物,培养主动建构的意识,发展学生的思维能力。例如,在教学“复式条形统计图”时,教师在引导学生探究过程中,可能会产生以下几个认知冲突。
冲突1:看两个图麻烦吗?(产生“合并”的需求。)
冲突2:竖着合并与横着合并哪个看起来更美观?(对比两种“合并方式”。)
冲突3:这张统计图横轴表示什么?纵轴表示什么?如何区分?(生成“图例”。)
学生在不断冲突中,将复式条形统计图建构完整。这样的思考过程是有趣的,学生能积极参与,通过分析评判,找到知识的本质,也促进思维向高阶发展。
三、借助操作,发展高阶思维
动手操作是发展学生思维、培养学生数学能力的有效途径。重视直观教学,是小学数学教材的特点之一,增强了实践活动和动手操作内容。所以,操作活动是数学课堂教学中的一个重要环节。
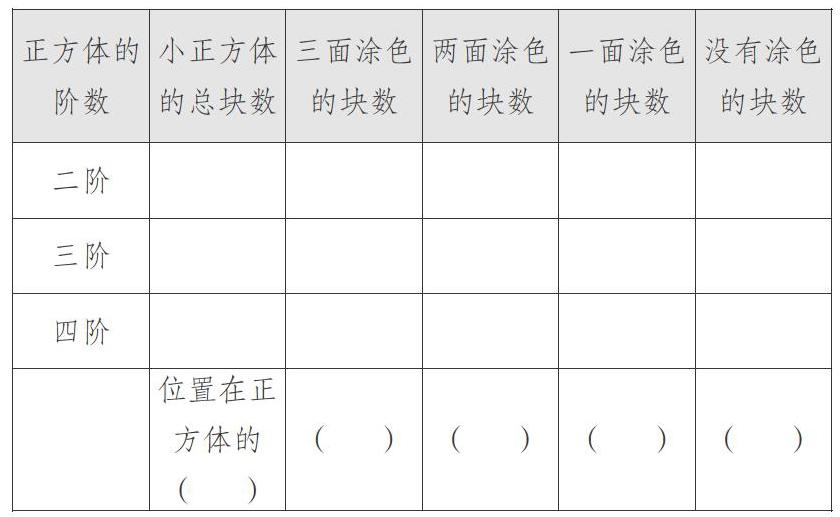
例如,在教学“探索图形”时,课中,教师抛出一个问题:这个12阶正方体中,每一类小正方体各有多少个呢?由于数学知识抽象,学生呈现出认知的困惑,感觉无从下手。教师循循善诱,首先引导学生从简单入手,利用手中的学具拆拼,多角度地观察、分析、概括,并填写好表格中的信息(如下表)。
有了这样的感知体验做基础,学生纷纷表达了自己观察分析后的想法,思维水平从感性上升到了理性。最后,教师引导学生归纳得出:三面涂色的小正方体都在大正方体的顶“点”的位置。不论棱长是几,分割后三面涂色的小正方体的个数都是8;两面涂色的小正方体都在大正方体的棱的位置,只要用每条棱中间两面涂色的小正方体的个数乘以12,就得出两面涂色的小正方体的总个数;一面涂色的小正方体都在大正方体的面的位置,只要用每个面中间一面涂色的小正方体的个数乘以6,就得出一面涂色的小正方體的总个数;没有涂色的小正方体处于大正方体的中间,只要用正方体总个数分别减去以上三类的小正方体个数即可。
教师显然不局限于文字的表征方式,大胆地进行设想:如果把棱长为n的涂色大正方体切割,三面涂色、两面涂色、一面涂色的小正方体各有多少个?引导学生用符号表征,这十分具有挑战性,有利于促进学生对数学知识的再创造。由于学生有了实践活动的认知基础,又有了初步推理做铺垫,学生纷纷表达自己的观点,在广泛交流后达成共识:三面涂色的小正方体个数为8;两面涂色的小正方体个数为(n-2)×12;一面涂色的小正方体个数为(n-2)2×6;没有涂色的小正方体个数为(n-2)3。这种借助实践活动的数学学习方式,丰富了学生的感性认知,为理性分析问题、解决问题提供了很好的条件。这样,无形中学生的思维水平也不断地提高,慢慢地向高阶思维迈进。
总之,培养学生高阶思维的策略见仁见智,问题驱动、提供思辨、动手操作等,无疑是培养学生高阶思维行之有效的策略。
(作者单位:福建省福清市岑兜中心小学)
