基于矩法的CRTSⅡ型轨道板裂缝宽度可靠性研究

童明娜，卢朝辉,2，赵衍刚，余志武

(1.中南大学 土木工程学院，湖南 长沙 410076；2.北京工业大学 建筑工程学院，北京 100022；3.神奈川大学 工学部，神奈川 横滨 221-8686)

根据我国2016年《中长期铁路网规划》[1]的规划目标，到 2020 年，我国铁路营业里程将增加至15万km，其中高速铁路3万km。与传统有砟轨道相比，高速铁路无砟轨道具有列车方便快捷、运输能力大等优势[2]，从而成为我国高速铁路的主流轨道结构，其中CRTSⅡ型板式无砟轨道结构大规模应用在杭长、京沪等10余条高速线路中。

我国现行的TB 10621—2014《高速铁路设计规范》[3]要求高速铁路主体结构设计使用年限不小于60年。此外，我国客运专线相关规范、验收标准规定，对于CRTSⅡ型板式无砟轨道结构的轨道板除预裂缝以外，其他部位不得有裂缝[4]。虽然CRTSⅡ型板式无砟轨道结构设置了横向贯通的预裂缝(也称为假缝)以控制裂缝的发展位置，然而，在实际运营过程中，由于无砟轨道结构受到列车荷载的反复作用以及日照气温升降、季节交替或其他自然环境的作用，仍然可能导致轨道板出现预裂缝外的开裂现象(见图1)。无砟轨道板开裂形成贯穿裂缝后容易导致钢筋锈蚀，从而影响轨道板的耐久性、适用性和安全性，同时裂缝达到一定宽度亦对列车运行的平稳性和舒适性造成了不良影响。鉴于此，一些学者针对轨道板混凝土结构的裂缝问题展开了研究：李志红[5]分析了轨道板混凝土裂缝产生机理，分别运用我国桥涵设计规范与混凝土结构设计规范中裂缝宽度的公式对双块式无砟轨道的裂缝宽度进行了计算；刘扬[6]分析了无砟轨道结构裂缝产生的原因，对CRTSⅠ型无砟轨道结构的裂缝宽度进行了检算，提出了无砟轨道裂缝检算的合理公式和裂缝检算宽度的取值；孙旭[4]进行了无砟轨道结构的开裂调查，建立了CRTSⅡ型板式无砟轨道二维离散元模型；赵林等[7]应用有限元法建立了CRTSⅡ型板式轨道的计算模型，分析了在不同荷载作用下宽接缝的开裂对CRTSⅡ型板式轨道受力性能的影响。

图1 某客运专线CRTSⅡ型轨道板非预裂缝处裂纹

以上研究者们均是在确定性条件下针对轨道板的裂缝问题进行的研究，然而，在实际工程中，列车荷载、温度作用、材料性能等均具备随机性。为了考虑随机不确定性因素的影响，张国虎[8]引入可靠度理论对CRTSⅡ型轨道板的裂缝宽度可靠性进行了研究，建立了轨道板裂缝最大宽度的功能函数，并利用蒙特卡洛方法循环1 000次对轨道板裂缝宽度的可靠性进行了评估，但是当循环次数较少时，蒙特卡洛法计算结果可能并不准确，并且当循环次数较多时相当耗时，因此，亟需运算简便且有效的方法来进行轨道板裂缝宽度的可靠度计算。

鉴于此，本文发展了轨道板裂缝宽度可靠度分析的四阶矩方法。首先，建立了温度作用及列车荷载共同作用下轨道板最大裂缝宽度的功能函数，接着结合一维减维点估计方法求解该功能函数的前四阶矩，然后依据四阶矩可靠度指标公式计算了可靠度指标及相应失效概率，探究了降温幅度对可靠度指标的影响，开展了CRTSⅡ型轨道板裂缝最大宽度的可靠度指标随温度梯度变化规律的研究。

1 轨道板裂缝产生的机理分析

轨道板裂缝产生的原因主要可分为两类：一是外荷载引起的结构裂缝，包括常规结构计算中的主要应力以及其他的结构次应力造成的受力裂缝；二是非受力变形引起的材料裂缝，主要是由温度荷载和混凝土收缩引起的[9]。

结构裂缝通常是由列车荷载引起的，文献[10]认为，在列车荷载作用下，CRTSⅡ型轨道板混凝土横向受拉应力远大于纵向受拉应力，约是其5倍，横向受拉应力较大会导致纵向裂缝产生，据此可以得出列车荷载主要引起纵向裂缝的结论。

温度荷载引起的材料裂缝的形成原因主要包括结构整体的温度升降差、水化热引起的混凝土内外温差以及结构从上表面至下表面的温度梯度[9]。

当混凝土结构随季节变化和日照周期变化时，结构整体发生均匀的温度升降变化，从而使混凝土结构发生伸缩。这种伸缩在没有纵向约束或约束很小时，产生的温度力可以不考虑。但是，由于CRTSⅡ型无砟轨道结构的横向存在预应力，同时混凝土结构伸缩受到的约束较弱，纵向无预应力，并且受很多纵向约束，因此可能导致混凝土出现横向的贯通裂缝。

混凝土结构在太阳照射下，其上表面温度较高，而下表面温度较低。由于混凝土导热性差，轨道板沿高度方向存在温度梯度，导致轨道结构翘曲，表面出现横向裂缝[4,9]。文献[11]分析表明，温度梯度作用下，轨道板混凝土的纵向应力是横向应力的2倍左右，纵向应力大会导致横向裂缝的产生。因此，本文认为，在温度梯度作用下，轨道板更容易产生横向裂缝，但也可能会产生纵向裂缝。

在上述原因中，水化热引起的材料裂缝和混凝土收缩裂缝可以通过采取优选原材料、减少用水量、改进施工工艺等措施来减少和避免，鉴于此，本文不将这两种裂缝作为轨道板裂缝的主要产生原因。

综合以上因素，轨道板产生横向裂缝的主要原因是结构整体的温度升降差和温度梯度作用，产生纵向裂缝的主要原因是列车荷载和温度梯度作用，轨道板横向裂缝及纵向裂缝示意见图2。

图2 轨道板裂缝示意图(单位：mm)

2 轨道板最大裂缝宽度功能函数的建立

根据GB 50010—2010《混凝土结构设计规范》[12]中对正常使用状态下混凝土结构构件裂缝宽度的验算要求，轨道板最大裂缝宽度的功能函数为

Z=[wlim]-wmax

(1)

式中：[wlim]为轨道板混凝土裂缝宽度限值；wmax为按作用的标准组合或准永久作用并考虑长期作用影响计算的最大裂缝宽度。

目前国内裂缝宽度的计算主要依据文献[12-13]，文献[6]对这两种结果进行检算，结果表明，文献[12]的设计结果中钢筋主拉应力过大，因而不适用于轨道板裂缝宽度检算，建议按照文献[13]中的公式进行计算。因此，本文选取文献[13]中的裂缝宽度公式来进行分析。

轨道板最大裂缝宽度计算模型为[13]

(2)

(3)

(4)

Ac1=2ab

(5)

式中：K1为钢筋表明形状影响系数，对光圆钢筋取1.0，带肋钢筋取0.8；K2为荷载特征影响系数；α为与钢筋表面有关的系数，对光圆钢筋取0.5，带肋钢筋取0.3；M1为可变作用下的弯矩；M2为永久作用下的弯矩；r为中性轴至受拉边缘的距离与至受拉钢筋重心的距离之比，板状结构可取1.2；σs为开裂处受拉钢筋纵向应力；Es为钢筋弹性模量；d为受拉钢筋直径；μZ为受拉钢筋的有效配筋率；Ac1为与受拉钢筋相互作用的混凝土面积，取为与受拉钢筋重心相重的混凝土面积；(φ1n1+φ2n2+φ3n3)As1为钢筋总面积，As1为单根钢筋的截面积；a为钢筋重心至受拉边缘的距离；b为受拉混凝土的矩形截面宽度。

当有预应力作用时，开裂处受拉区纵向钢筋应力为

(6)

(7)

(8)

ep=yp-ep0

(9)

式中：Mk为考虑荷载组合后的弯矩；Ap为受拉区纵向预应力筋的截面面积；As为受拉区纵向普通钢筋的截面面积；h0为截面有效高度；α1为预应力筋的等效折减系数；Np0为计算截面混凝土法向预应力为0时的预应力；ep为当混凝土截面的法向预应力为0时，Np0作用点到纵向预应力筋与普通钢筋合力点之间的距离；ep0为计算截面混凝土法向预应力为0时，Np0作用点的偏心距；z为受拉区纵向普通钢筋与预应力钢筋合力点到截面受压区合力点之间的距离；yp为受拉区纵向预应力筋与普通筋合力点的偏心距。

当无预应力作用时，开裂处受拉钢筋纵向应力为

(10)

开裂处受拉区钢筋应力的求解是较为关键问题。CRTSⅡ型轨道板横向采用单层先张的预应力体系，设置60根直径为10 mm螺旋肋预应力钢丝，纵向采用6根直径为20 mm的精轧螺纹钢筋连接成整体，纵、横向钢筋的上、下层分别配置一层钢筋网片，所有钢筋交叉点均做绝缘处理[14]。考虑到CRTSⅡ型轨道板的配筋情况及构造特征，横向裂缝宽度计算时采用式(10)，其中Mk要考虑轴向均匀温度的变化以及温度梯度作用引起的弯矩组合；纵向横向裂缝宽度计算时采用式(6)，其中Mk要考虑列车荷载以及温度梯度作用引起的弯矩组合。

2.1 列车荷载引起的钢筋应力计算

列车荷载弯矩通常采用有限元模型来进行求解，有限元分析模型主要包括梁板有限元模型、3D实体有限元模型和弹性地基-叠合梁体系模型，孙璐等[15]针对此三种模型的分析的轨道板横、纵向弯矩进行比较分析得知：梁板有限元模型在求解列车荷载效应具备高效准确之优势，文献[16-18]也有类似的结论。鉴于此，本文亦选用梁板有限元模型分析列车荷载弯矩，图3为无砟轨道梁板理论的有限元分析模型(红色箭头表示列车竖向轮轨力)，模型中扣件采用三个方向的弹簧模拟，三个方向的扣件刚度分配值如图3(a)中A所示(图3(b)为放大图)；CA砂浆层及下部基础的竖向支承作用采用连续均匀的线性弹簧模拟。分析有限元模型所用到的参数见表1。

列车荷载弯矩为[17]

Mv=Mv(P,Eg,Ek,Eq)

(11)

式中：P为列车竖向轮轨力；Eg为轨道板弹性模量；Ek为扣件刚度；Eq为桥面弹簧刚度系数。P、Eg、Ek和Eq均视为随机变量。

将式(11)中的列车荷载弯矩代入式(6)中，即可求解出列车荷载引起的钢筋应力。

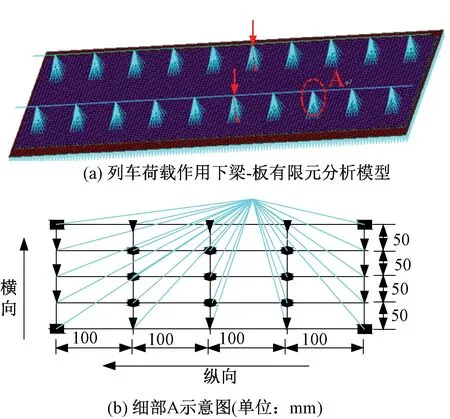
图3 轨道板梁-板有限元模型示意图

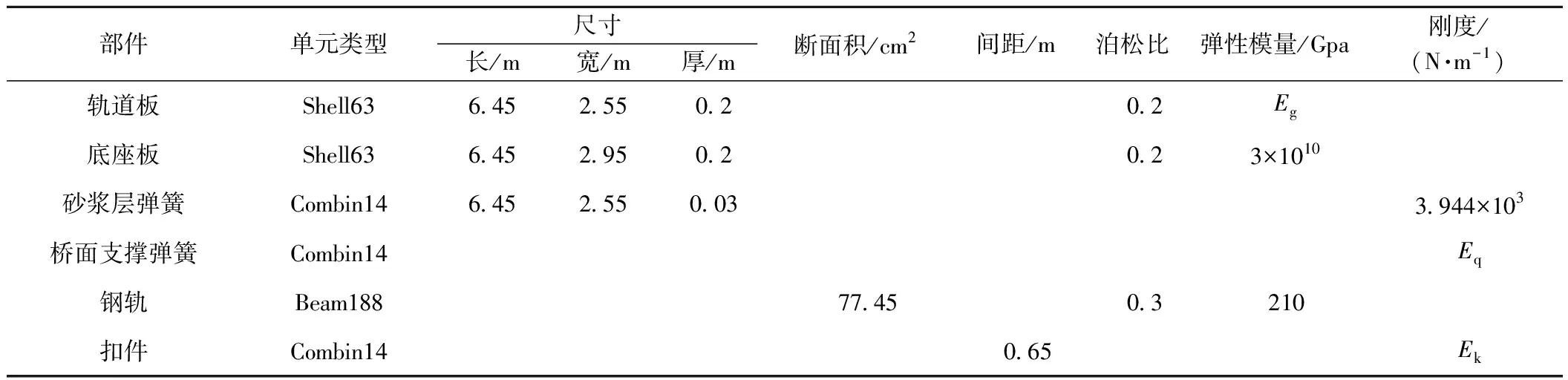
表1 梁-板有限元模型各参数取值

2.2 轴向均匀温度变化引起的钢筋应力计算

文献[19]将混凝土梁板的非线性温度分布分解为三部分：轴向均匀温度(整体温差)、线性温差(温度梯度)和非线性温差。其中，非线性温差部分只对混凝土梁板产生自平衡应力，对整个结构没有产生荷载效应。根据GB 50009—2012《建筑结构荷载规范》[20]中的规定，温度荷载对混凝土的影响普通梁板结构尺寸主要考虑均匀轴向温度变化的影响和线性温度梯度变化的效应，而非线性温差所产生的内部压力通常可以通过合理的方法进行修正。我国无砟轨道结构设计中温度作用主要考虑了轴向温度作用和温度梯度作用。

轴向均匀作用引起的钢筋应力为[10]

σs(t)=(αTλst-αs)EsΔT

(12)

2.3 温度梯度作用引起的钢筋应力计算

文献[10]指出，温度梯度作用引起的弯矩可按照威氏公式来计算解析解。根据此解析解得知：当轨道板处于正温度梯度时，轨道板呈“凸”字变形状态，此时轨道板顶面混凝土及上层纵向钢筋处于受拉状态，底面混凝土及下层纵向钢筋处于受压状态，当轨道板处于负温度梯度作用时，轨道板变形和受力状态则与正温度梯度作用下大致呈对称状态；同时部分研究者们[21-23]利用有限元分析技术，求解了轨道板在温度梯度作用下的变形与受力状态，得出与威氏公式较为接近的结论，为了计算上的方便，李怀龙等[24]将威氏公式进行了进一步简化为

MW=KtT

(13)

式中：T为温度梯度；Kt为温度弯矩系数。

综上，考虑轴向均匀温度作用和温度梯度作用的CRTSⅡ型轨道板横向裂缝宽度的功能函数为

(14)

考虑横向预应力、列车荷载和温度梯度作用的CRTSⅡ型轨道板纵向裂缝宽度的功能函数为

(15)

3 随机变量分析

针对无砟轨道结构中的随机变量参数，一些学者做了相关研究分析：赵磊等[11,25]认为列车竖向轮轨力作为结构中存在的主要随机源之一，其服从均值为300 kN，变异系数为0.15的正态分布；刘学毅等[16]认为轨道板混凝土弹性模量服从均值为3.29×104，变异系数为0.08对数正态分布；桥面刚度系数服从均值为109，变异系数为0.05的对数正态分布；张国虎[8]认为钢筋弹性模量服从均值为2.1×105，变异系数为0.06的正态分布；李怀龙等[24]认为温度弯矩系数服从均值为0.162 5，变异系数为0.035的正态分布；温度梯度服从变异系数为0.3的威布尔分布。文献[26]在桥上CRTSⅡ型板式无砟轨道的线路上建立温度场自动监测系统，实测温度梯度变化范围为-36～73 ℃/m，为探究温度梯度对轨道板裂缝宽度可靠度指标的影响，本文将温度梯度T的均值取-36～73 ℃/m间不同的值来进行分析。

我国铁路设计规范尚未给出CRTSⅡ型板的设计温降值，文献[27]中将连续配筋混凝土路面的设计降温幅度近似取为路面施工的月份日最高温度和一年中最冷月份日最低温度月平均值之间的差值，以北京地区为例，降温幅度最大值约35 ℃，考虑到地域之间的差异大，认为降温幅度服从变异系数0.2的正态分布。为探究降温幅度对轨道板裂缝宽度可靠指标的影响，本文分别选取降温幅度的均值10、20、35 ℃进行计算。

TB 10002.3—2005《铁路桥涵钢筋混凝土和预应力钢筋混凝土结构设计规范》[13]中规定，无砟轨道允许裂缝宽度限值取为0.2 mm；GB 50010—2010《混凝土结构设计规范》[12]同时规定，当环境类别为二类或三类时，钢筋混凝土结构构件的最大允许裂缝宽度为0.2 mm。鉴于此，本文选取轨道板裂缝宽度限值为0.2 mm，并定义其服从变异系数为0.1的正态分布。

本文用到的随机变量分布特征及常量分别见表2和表3。

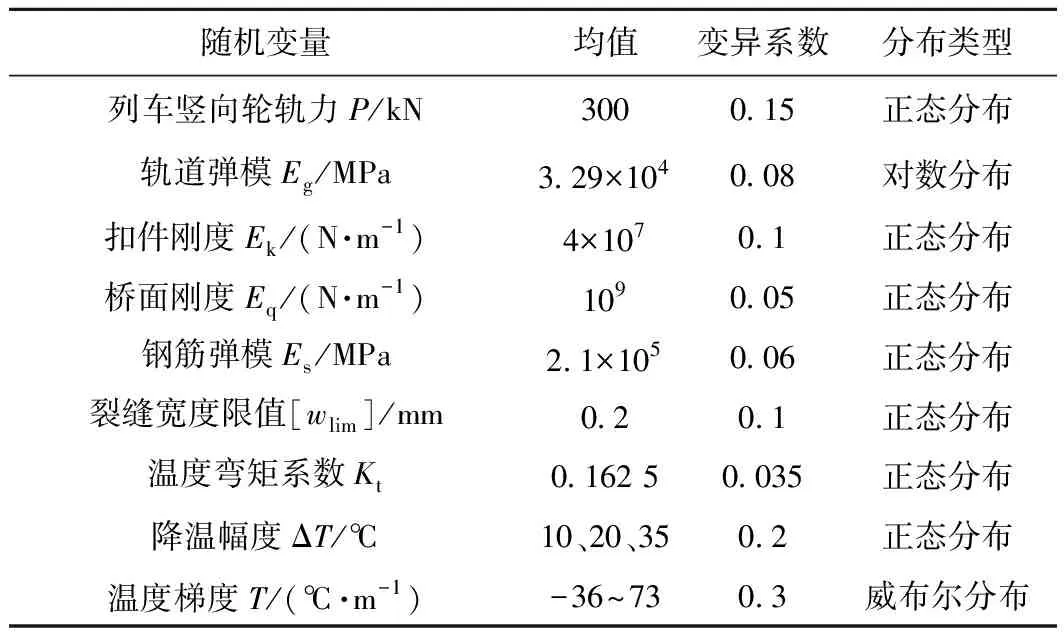
表2 随机变量分布特征表

表3 常量取值表

4 基于矩法的轨道板最大裂缝宽度可靠度

近年来，矩法因具有高效、准确且易与有限元结合的特点而被应用于无砟轨道结构可靠度分析[17-18]，研究表明矩法在很大程度上能取代一次二阶矩法(FORM)、蒙特卡洛(MCS)等可靠度分析方法。矩法计算可靠度分为以下两个主要步骤[28]：首先，采用点估计结合一维减维的方法进行计算功能函数的前四阶矩；然后，将前四阶矩代入可靠度计算公式。

4.1 点估计结合一维减维方法

本文首先以轨道板横向裂缝为例来说明矩法结合一维减维的计算过程。

首先计算降温幅度均值为35 ℃的情况，取温度梯度T的均值为45 ℃/m。

轨道板横向裂缝宽度的功能函数如式(14)所示，记Z1=G(X)，将随机变量Es、[wlim]、Kt、T和ΔT记为x1、x2、x3、x4和x5，即n=5。

根据标准正态空间上的7点估计一维减维的方法[28]，式(14)可写为

(16)

式中：

Gμ=G(μ1,μ2,μ3,μ4,μ5)=

(17)

G1=G(x1,μ2,μ3,μ4,μ5)=

(18)

G2=G(μ1,x2,μ3,μ4,μ5)=

(19)

G3=G(μ1,μ2,x3,μ4,μ5)=

(20)

G4=G(μ1,μ2,μ3,x4,μ5)=

(21)

G5=G(μ1,μ2,μ3,μ4,x5)=

(22)

G(X)前四阶矩为[28]

(23)

(24)

(25)

(26)

式中：μGi、σGi、α3Gi、α4Gi分别为单变量函数Gi的前四阶矩。

(27)

(28)

(29)

(30)

式中：T-1(uik)为第i个随机变量的第k个逆正态转换值；uik(k=1,…,7；i=1,2,3,4,5)为ui的第k个估计点；pk为相应的权重，估计点值uik及相应的权重pk见表4[28]。

表4 估计点uik及相应的权重pk值

4.2 四阶矩可靠度指标及失效概率计算

根据4.1节中的步骤得到功能函数的前四阶矩后，可进行可靠度指标及失效概率的计算[29]

(31)

Pf=Φ(-β4M)

(32)

;

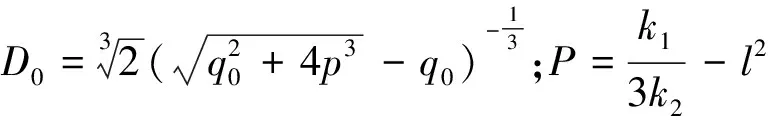
为了保证l2存在，根号内的数必须为正值，因而必须

(33)

4.3 轨道板最大裂缝宽度可靠度结果分析

根据表2中随机变量的分布特征及表4中标准正态空间的7点估计值，可以求得随机变量的7点逆正态转换值，见表5。

表5 随机变量7点逆正态转换值表

将表2中xi(i=1, 2, 3, 4, 5)均值、表3常数项代入式(14)得Gm=0.023 57 mm。

将表5中x1的7点逆正态转换值、表2中的均值及表3中的常数项代入式(27)～式(30)可计算得到G1的前四阶矩分别为：0.022 928 mm、0.010 742 mm、-0.369 96、3.277 157。

同理可得到Gi(i=1, 2, 3, 4, 5)的前四阶矩，如表6所示。

将Gm、表6中Gi(i=1, 2, 3, 4, 5)的均值、方差、偏度和峰度代入到式(23)～式(26)，可以得到：μG=0.022 928 mm；σG=0.022 702 3 mm；α3G=-0.039 184；α4G=3.014 587。然后将得到的前四阶矩(μG、σG、α3G、α4G)分别代入式(31)和式(32)中，得到可靠指标β=1.009 94，失效概率Pf=0.156 262。采用蒙特卡洛法(100万次)求得横向裂缝宽度的可靠指标为1.016 45，两者结果非常接近，而采用本方法仅需计算21次，这表明采用本文方法进行可靠度计算可以提高计算效率、减少计算次数，同时保证计算结果的精度。

图4 轨道板横向裂缝的可靠度指标随温度梯度均值的变化值

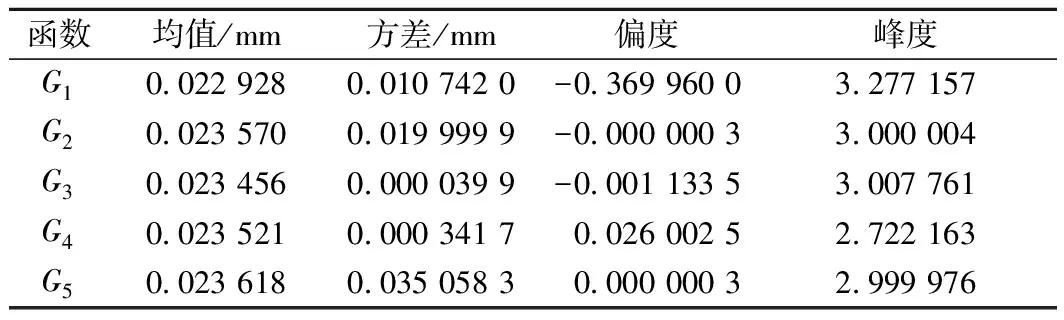
表6 Gi前四阶矩

正温度梯度作用下，轨道板上层纵向钢筋处于受拉状态，下层纵向钢筋处于受压状态；当轨道板处于负温度梯度作用时，轨道板上层纵向钢筋处于受压状态，下层纵向钢筋处于受拉状态。轴向均匀温度的作用下，轨道板钢筋处于受拉状态。由于正温度梯度最大值(73 ℃/m)大于负温度梯度最大值(-36 ℃/m)，因此正温度梯度作用下引起的钢筋应力值大于负温度梯度引起的钢筋应力值，为考虑最不利情况，本文主要计算轨道板上层纵向钢筋应力。当考虑温度梯度与轴向均匀温度综合作用时，正温度梯度情况下，将正温度梯度引起的钢筋应力与轴向均匀温度引起的钢筋应力相加来进行计算；负温度梯度情况下，将正温度梯度引起的钢筋应力与轴向均匀温度引起的钢筋应力相减来进行计算。

将温度梯度T的均值取不同的值(-36～73 ℃/m)，同时考虑温度梯度作用与轴向均匀温度作用的叠加，重复上述方法可得到降温幅度为35 ℃轨道板横向裂缝宽度的可靠度指标随温度梯度的变化，并利用蒙特卡洛方法进行对比，结果如图4(a)所示。

同理，可分别得到降温幅度的均值为20 ℃和10 ℃时轨道板横向裂缝宽度的可靠度指标随温度梯度的变化见图4(b)和图4(c)。

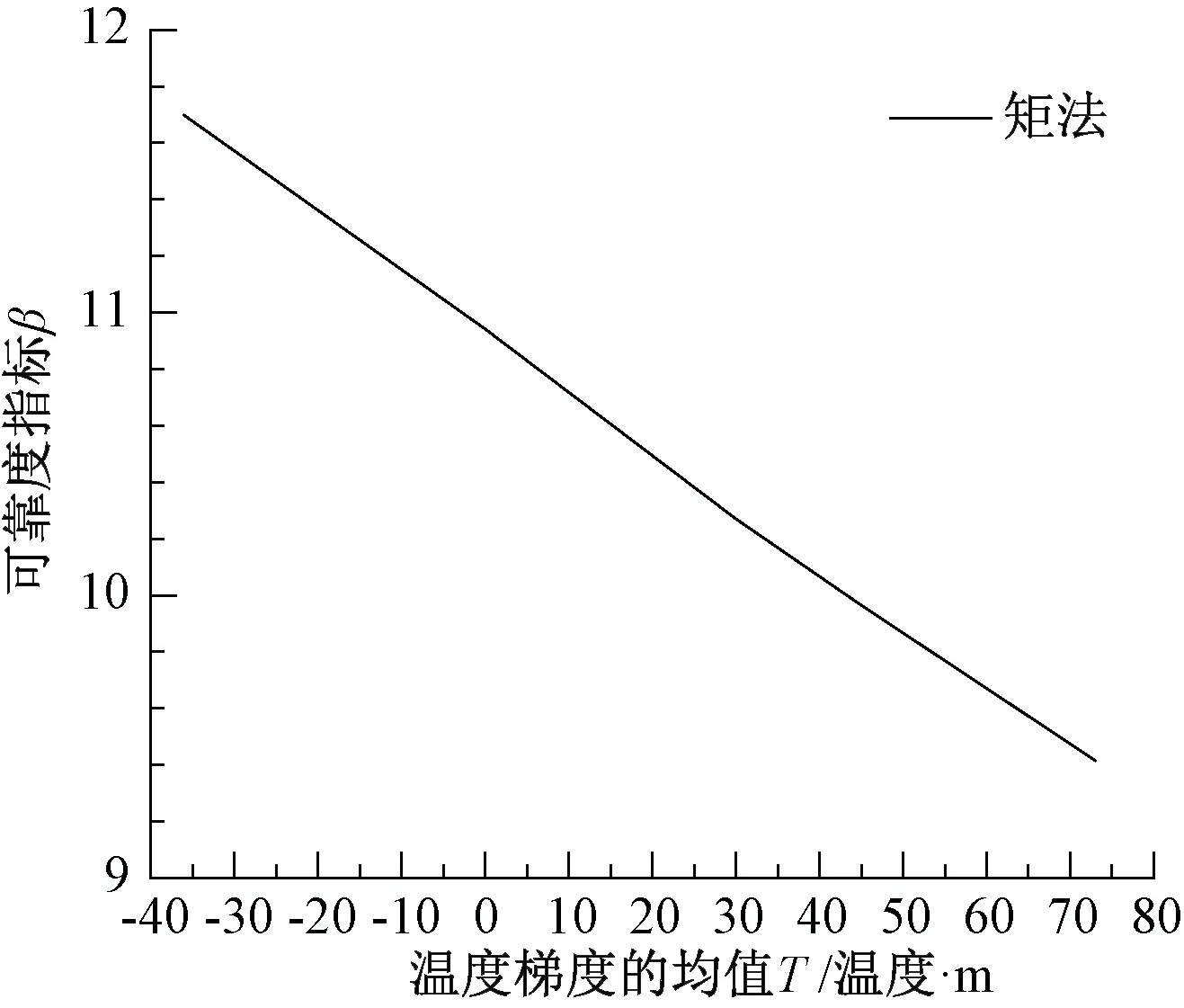
图5 轨道板纵向裂缝的可靠度指标随温度梯度均值的变化值

文献[17]和文献[18]中矩法结合有限元的方法，将温度梯度的均值T取不同的值(-36～73 ℃/m)，重复上述步骤，即可得到轨道板纵向裂缝宽度的可靠度指标随温度梯度的变化，见图5。

参照Q/CR 9007-2014《铁路工程结构可靠性设计统一标准》[30]中规定的轨道结构正常使用极限状态的可靠度指标建议值，将CRTSⅡ型轨道板裂缝宽度的目标可靠度指标取为2.5。

由图4及图5中可知，轨道板裂缝宽度随温度的变化规律：CRTSⅡ型轨道板纵向裂缝宽度可靠度指标在常见温度梯度区间内均大于9，相应的失效概率几乎为零，这说明纵向裂缝基本不会发生宽度超限的现象。CRTSⅡ型轨道板横向裂缝宽度可靠度指标与降温幅度有关，当降温幅度的均值为10 ℃时，且在常见温度梯度区间内，可靠度指标大于6，相应的失效概率小于9.8×10-10，说明轨道板处于安全状态；降温幅度的均值为20 ℃时，可靠度指标β∈[3.986 47, 6.716 24]，相应的失效概率Pf∈[9.32×10-12, 0.000 033 531 8]，这表明在常见温度梯度区间内，可靠度指标大于目标可靠度指标，可认为轨道板处于安全状态；降温幅度的均值为35 ℃时，在常见温度梯度区间内，β∈[0.376 87, 2.730 95]，Pf∈[0.003 157 6, 0.353 135]，轨道板裂缝超限的概率极大，尤其是温度梯度的均值大于-25 ℃/m时，可靠度指标已经低于规范要求，轨道板结构存在很大的安全隐患，裂缝宽度超限容易使钢筋腐蚀加剧，从而造成结构加速破坏，同时裂缝宽度过大会影响轨道结构的耐久性，可能会对行车安全造成影响，建议加强轨道板的维护与管理。

5 结论

本文在分析轨道板横向裂缝及纵向裂缝产生原因的基础上，建立了温度作用及列车荷载共同作用下CRTSⅡ型轨道板横向及纵向最大裂缝宽度可靠度分析的功能函数。采用四阶矩可靠度方法对此功能函数进行了可靠度分析：结合一维减维点估计方法，采用四阶矩可靠度指标公式计算了相应可靠度指标及失效概率，探究了可靠度指标随温度梯度的变化规律。分析结果表明：

(1) 本文采用的四阶矩可靠度方法具有易与结构有限元分析技术相结合、计算效率高以及计算结果准确等优点，表明该方法适用于轨道板最大裂缝宽度的可靠度分析。

(2) 轨道板纵向裂缝宽度发生超限的概率极小，降温幅度较大时横向裂缝宽度超限的概率较大，容易使钢筋腐蚀加剧，从而造成结构加速破坏，同时裂缝宽度过大会影响轨道结构的耐久性，可能会对行车安全造成影响，因此建议加强轨道板的维修养护。