一种高压直流输电系统运维策略的优化方法*

王 鑫 宋广磊 李昱萱

（国网新疆电力有限公司信息通信公司 乌鲁木齐 830000）

1 引言

变压器是高压直流输电系统（HVDC）中的关键设备，由于空载电力变压器铁芯具有饱和的励磁特性，一旦其磁化，电压容易发生突变，就会产生含有大量谐波的涌流［1］。励磁涌流会引起系统电压畸变和其他不利的系统运行问题，例如电能质量恶化以及对保护系统的干扰或误操作［2］。当励磁变压器与存在大量并联电容器系统或HVDC 的RPC滤波器组连接时，由于励磁涌流的谐波与系统并联谐振频率之间的谐振相互作用，电压畸变发生概率和严重性将增加［3～4］。文献［5］指出在系统恢复期间，由于并联谐振的存在，励磁变压器可借助长传输链路连接到相对较弱的配电网系统中。在这种并联谐振下，如果系统出现高阻抗，则电压畸变将放大并延长。如果不采取必要的限制或预防措施，则过电压将会损坏绝缘并导致系统的设备寿命缩短。针对这一严重后果，对变压器励磁涌流已经进行了大量的研究，并引入了许多不同的方法和装置来降低通电期间变压器的励磁涌流。最常见的方法是应用具有受控开关技术的合闸角检测（POW）装置［6］。文献［7］在变压器通电期间通过中性电阻开关来控制涌流。文献［8］基于电力电子设备来抑制涌流。然而，在这种设备投入使用之前，仍然需要人为操作实现实时运维。

本文旨在对HVDC运维策略进行优化，提出了变压器励磁涌流与系统并联谐振相互作用的分析方法。利用HVDC 中现有的RPC 装置间接地使系统并联谐振频率发生偏移，从而避免变压器励磁涌流的谐振效应。仿真结果证明了该方法可用于降低变压器励磁涌流对HVDC系统运行的影响。

2 变压器励磁涌流

2.1 电磁模型

变压器励磁过程中的瞬态涌流的等效电路，如图1 所示。变压器的等效初级电阻和漏抗分别为Rtx1和Ltx1。忽略铁芯损耗，磁化回路由非线性电感器Lm(Φ)表示，其中Φ 是具有磁化电流（I）映射特性的磁通量，变压器的磁通量与磁化电流的关系，如图2 所示。其中，Im和Φm分别为磁化电流和磁通量的最大值。

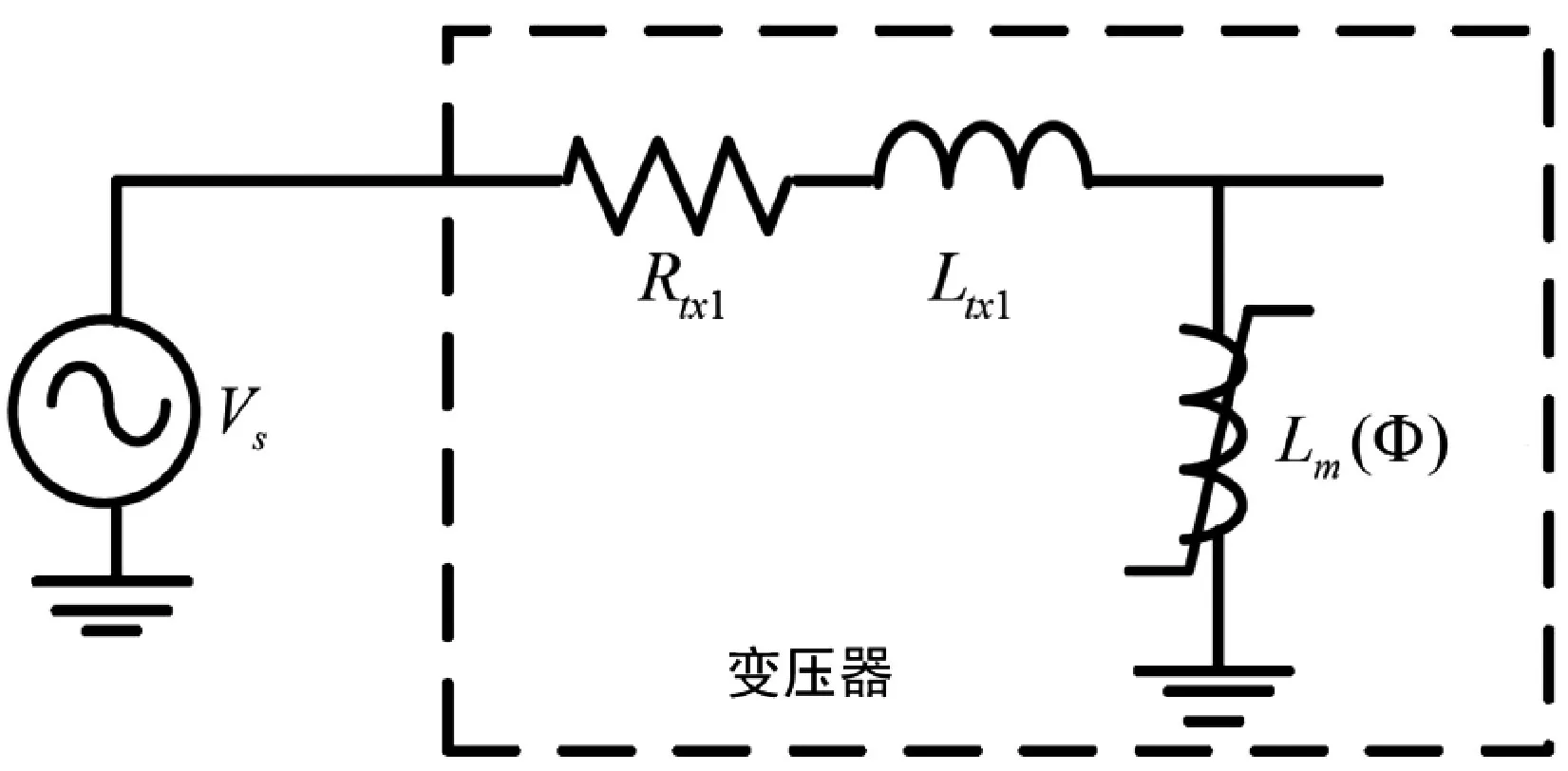
图1 变压器励磁的瞬态涌流等效电路

图2 变压器的磁通量与磁化电流的关系

铁芯中的磁通量Φ 与所施加的电压VLm的关系如下：

其中，N 是铁芯上的线圈匝数。

变压器电压的微分方程形式可以描述为

由于施加在初级绕阻的电压形式为

其中，Vm是施加电压的幅值，θ 是电压的初始相位角，ω 是系统频率。将电抗Lm(Φ)线性化为等效恒定电抗Lm，因此，电流为

将式（3）和式（4）代入式（2）中，假设初始电流i(0)=0，剩余磁通Φ(0)=Φ0，可以求解微分方程得到变压器磁通量的表达式：

其中

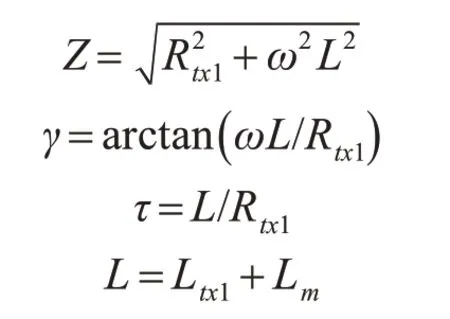
2.2 励磁涌流的影响因素

根据电流与磁通量之间的非线性关系，变压器励磁涌流主要由以下因素决定［9～12］：1）变压器铁芯的饱和特性，如B-H 曲线；2）变压器通电时的电压波形；3）变压器中剩余磁通量；4）变压器的阻抗，它影响励磁涌流的峰值幅度和衰减持续时间；5）施加到变压器上的电压大小。

变压器通电过程中将引起电源电压、磁通量以及励磁涌流的变化，如图3 所示。假设剩余磁通量Φ0为正，变压器在t1时刻通电，此时电源电压处于零交叉点，如图3（a）所示的电压从具有相同极性的剩余磁通量产生电压。在图3（b）中，铁芯磁通在t2时刻达到最大值，此时正电压的整个半周期结束。如图2 所示，磁通量曲线具有非线性相对磁导率，则饱和磁通可导致较大的励磁涌流。因此，励磁涌流含有大量的谐波，如图3（c）所示。并且这些谐波可分为奇数阶谐波和偶数阶谐波分量，如图4 所示。随着谐波阶数的增加，励磁涌流的幅值减小。

2.3 励磁涌流中的谐波

对于给定的变压器，包含h 阶谐波的励磁涌流可表示为

其中，α 是变压器相位系数。

图3 变压器能量曲线

图4 变压器励磁涌流的幅值

如果没有POW 装置，很难应用精确的α 来限制励磁涌流。然而，励磁涌流中每个谐波分量的最大冲击情况发生在其峰值幅度时，因此，可以在α=π/h 时获得包含h 阶谐波的最大励磁涌流：

其中，Wh为变压器励磁涌流中h 阶谐波的加权因子。

3 系统并行谐振

3.1 系统配置与模型

除了励磁涌流的影响以外，交流电压畸变的严重程度还取决于并联谐振时的系统阻抗［13］，而并联谐振时的系统阻抗主要取决于HVDC 变换站的电网阻抗模型、输电线路和无功补偿装置（RPC）。本文所研究的系统配置如图5所示。

图5 系统配置

对于三相短路电平，将电网简化为具有戴维南等效阻抗节点［14］。由于系统中的电容能够改变系统的谐振频率，则传输线路建模为PI 型线路。HVDC 的运维组件由两部分构成：转换组件和RPC装置。本文将重点分析励磁涌流与系统并联谐振的相互作用，从而将HVDC运维简化为基频可编程的PQ源。

3.2 HVDC运维中的RPC

RPC 装置在改变系统谐振频率方面起着重要作用。交流滤波器（AC滤波器）作为基于晶闸管的HVDC 电力传输所需的RPC 器件，此类HVDC 变换器可产生具有h=np±1 阶的交流谐波，其中n 是整数，p 是变换器的脉冲数量。双调谐和三调谐交流滤波器（A 型和B 型）为变换器产生的谐波电流提供低阻抗路径，而避免谐波影响扩散到配电网系统中。此外，AC 滤波器可以为功率变换器提供必要的无功功率（Var）。本文应用的另外两种RPC装置是并联电容器（C型）和并联电抗器（SR型），它们分别提供和吸收额外的Var，并与HVDC 运维的AC滤波器一起工作。在正常情况下，线路换向变换器（LCC）的无功功率与实际功率成正比。文献［15］根据HVDC负载和运维条件，为RPC装置设计了几组预定义的开关表，即在不同的功率传输水平和条件下，采用滤波器组、并联电容器和并联电抗器的不同组合来实现谐波的最小化，并满足HVDC运维和AC系统之间无功功率净交换的要求。

3.3 系统阻抗的频率响应

系统的并联谐振由电网、传输线路和并联补偿RPC 装置决定。对于系统阻抗分析，图5 的等效电路可以简化为图6。

图6 系统阻抗的等值电路

励磁变压器可视为谐波源I(s)。整个电网等效导纳Ytot(s)可以从由励磁变压器双端口系统的每个并联等效支路计算：

其中，Ygrid(s)是与传输线路串联的电网导纳，而是正在运行的RPC装置总导纳。

为了说明并联谐振的变化，在表1 前两列列出了HVDC 的运维条件。系统阻抗与频率特性曲线的关系，如图7 所示。B 型滤波器用于滤除3、5、11阶谐波。电网短路电平选用9000MVA（基频为60Hz）的两条500kV，65km 长的输电线路并联组成。

表1 RPC双极开关表

图7 系统阻抗与频率关系

图7 表明，随着HVDC 负载的增加，系统谐振频率间接地转移到较低频率区域。相应的并联谐振阻抗也随着使用的RPC 滤波器的数量减少而降低。在两个A 型滤波器和1 个B 型滤波器条件下，不同短路电平的系统阻抗与频率的关系，如图8 所示。随着系统短路电平的增加，系统谐振频率将增加。

图8 不同短路电平的系统阻抗与频率的关系

3.4 电压畸变的评估

并联谐振可以放大滤波器的谐波分量，而这些谐波分量并不是滤波器所产生的，而是存在于励磁涌流中。如果励磁涌流中的谐波与具有高阻抗的谐振点一致，则谐波的谐振会引起电压畸变。基于上述分析，本文提出了电压畸变指数Dindex用于评估不同运维方式下总畸变的严重程度：

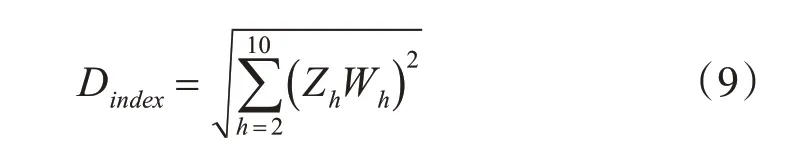
其中，Zh是h 阶谐波下的系统阻抗，畸变指数考虑了第二次谐波到第十次谐波。

计算得到的Dindex列于表1 的第三列中，最大畸变指数（Dindex=60.68）表明，在给定条件下，当HVDC 负载P 达到满额负载的比例在［0，10%］范围内运行时，预期的电压畸变最严重。在这种情况下，应避免给变压器供电的操作。

本文还建立了电压畸变索引表以便于快速进行严重性检查。表2 总结了三个选定的HVDC 运维工况下的畸变指数。在模型中，可以通过改变在线发电机组的数量或配电网拓扑来实现。结合图8所示，在短路电平为11000MVA的2A1B拓扑结构情况下，峰值阻抗出现在第4 阶谐波处。与相同2A1B拓扑下的其他较低短路电平方案相比，在第4阶谐波处的这种峰值阻抗将会导致较高的畸变指数（Dindex=89.59）。通过表2 的数值，操作人员可以选择适当的方案来控制空载变压器，进而达到对HVDC系统运维的优化。

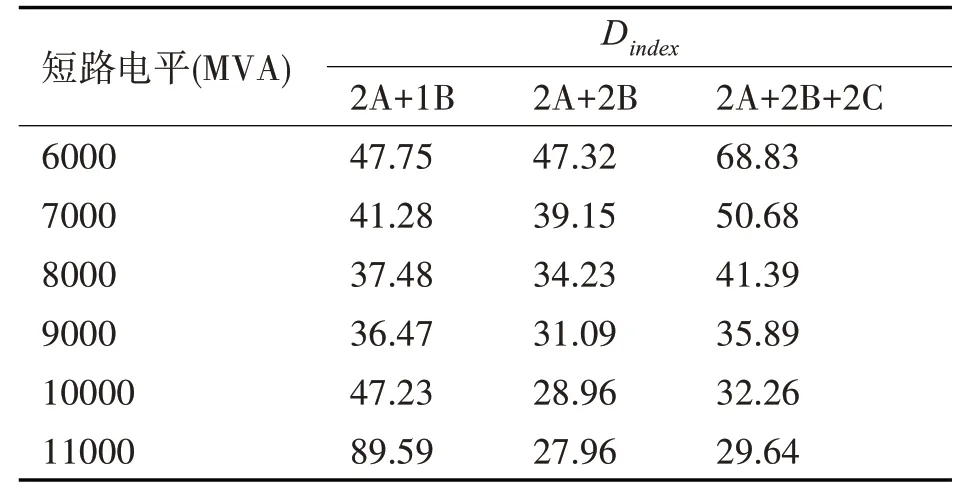
表2 HVDC运维的畸变指数

4 仿真实验

4.1 无优化的变压器接入

本文利用数字仿真检验所提方法的分析结果。在仿真中，禁用了HVDC 运维的所有保护装置。利用图5中的系统拓扑结构和图7中使用的参数，在变压器接入之前，系统在40%的HVDC 负载下呈现稳定，其中两个A 型滤波器正在运行。在t=2.06s，空载变压器接入。短路电平为9kMVA，40%的HVDC 负荷（2A）时的A 相过电压和励磁涌流如图9所示。

图9（a）可见A 相上发生的过电压在接入过程中呈现较大波动，这是由于谐振导致过电压波动持续时间延长。图9（b）中的励磁涌流由于变压器饱和而达到3.0pu。在2.90s～3.10s的范围内相应的三相电压如图10 所示。图10 中的电压波动较大，进而说明了电压畸变的严重性。

图9 短路电平为9kMVA，40%的HVDC负荷（2A）

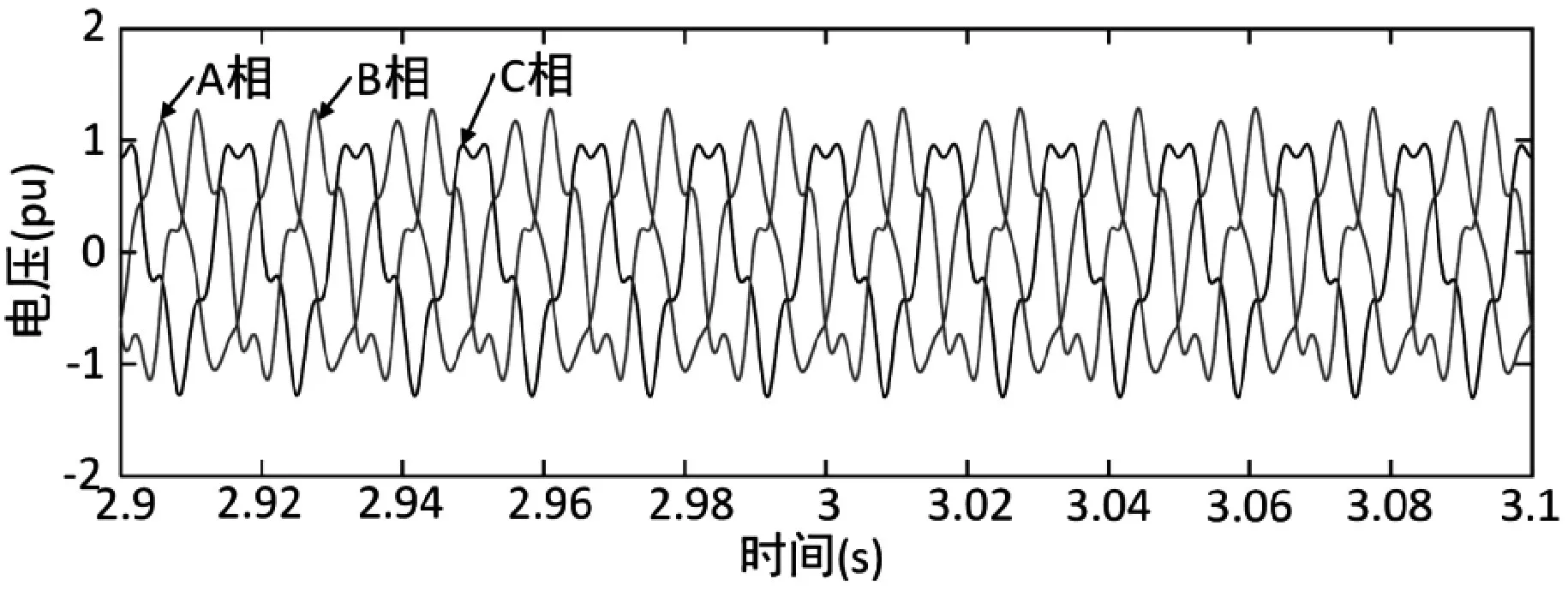
图10 三相电压的畸变

4.2 低畸变指数的变压器接入

从表1 所示的分析结果中可以看出，如果短路电平在不改变配电网配置的情况下保持不变，则在2A2B情况下出现最小畸变指数（即Dindex=31.09）。在HVDC 负载增加到60%时，采用相同的模拟进行试验，其中两个A 型滤波器和两个B 型滤波器正在运行，并且在t=2.06s，空载变压器接入。短路电平为9kMVA，60%的HVDC 负荷（2A2B）时的A 相过电压和励磁涌流如图11所示。

图11 短路电平9kMVA，60%的HVDC负荷（2A2B）

图11 （a）可见A相上发生的过电压在接入过程中电压畸变保持在较低水平。图11（b）表明变压器接入后最大励磁涌流达仍然能够达到相同水平（3.0pu）。具有最大总谐波失真（THD）在2.04s～2.24s 的范围内三相电压波形如图12 所示。与图10 中所示的波形相比，图12 中没有严重的过电压畸变。

图12 具有最大总谐波失真（THD）的三相电压

5 结语

本文旨在对HVDC运维策略进行优化，提出了定量分析变压器励磁涌流对HVDC 系统并联谐振影响的方法。该方法能够方便运维人员评估变压器接通时引起的电压畸变严重程度。利用最小电压畸变指数调整HVDC负载和相关的RPC装置，间接地转移系统并联谐振，从而避免或减少与变压器励磁涌流的相互作用，仿真结果验证了分析结果和缓解方案的有效性。