基于神经网络算法的电感参数辨识在弱磁控制中的研究*

刘 钰 刘文生 张皓淼

（1.大连交通大学 大连 116028）

（2.国网新疆电力有限公司电力科学研究院 乌鲁木齐 830011）

1 引言

内置式永磁同步电机（Interior Permanent Mag⁃net Synchronous Motor，IPMSM）具有体积小、效率高、转矩电流比大、功率密度高以及调速范围宽等优点，在电动汽车、工业控制等领域得到了越来越广泛的应用。电机运行过程中，其调速性能的优劣受电机参数的影响较大，而电机参数又会受温度变化、磁路饱和以及电机老化等因素的影响而发生改变［1～2］。在线获得精确的电机参数有利于实时校正电机控制器参数以达到更好的调速性能。因此，永磁同步电机参数在线辨识技术受到了国内外学者的广泛关注，已成为电机控制领域的研究热点之一［3～4］。

目前，常见的辨识算法主要有模型参考自适应法、卡尔曼滤波法、最小二乘法以及人工智能法等方法。文献［5］针对综合粒子群算法后期搜索效率低的缺陷，引入增长率因子，仅需采样电机的定子电流、电压和转速信号。文献［6］提出了一种基于线性元件的神经网络辨识方法，但此方法用估算的磁链值反推电阻值，误差相对较大。文献［7］针对表贴式永磁同步电机，在神经网络解耦辨识算法的基础上，在d 轴注入负序电流，实现了电感、电阻和磁链的辨识。文献［8］基于模型参考自适应理论，通过采用分步辨识法辨识出定子电阻和转子磁链，保证了辨识结果的唯一性。文献［9］则在模型参考自适应方法中加入了低通滤波器，进而减少了高频噪声对辨识参数的干扰。文献［10］采用带遗忘因子的递推最小二乘法对电感参数进行在线辨识，并将辨识的结果应用到基于电压前馈的电流解耦算法中，但是无法彻底消除旧数据对数据估算带来的误差。文献［11］采用高频信号注入法进行电感参数辨识，并提出变参数最大转矩电流比（Maximum Torque Per Ampere，MTPA）的控制策略，并由此建立转矩-电流最优控制表并预先存储于控制表中，转矩的控制精度较高，但是高频信号注入法适用于转速较低的情况下，具有一定的局限性。文献［12］提出了基于矢量控制技术的d 轴复合电流激励法和转矩调整法的d-q 轴电感辨识算法，并考虑到逆变器非线性因素，对输出电压误差进行补偿。文献［13］提出了一种基于增量式的模型参考自适应的电感在线辨识算法。文献［14］以扩展卡尔曼滤波算法计算出的电机参数作为训练样本，然后训练神经网络辨识电机参数，训练速度较快但是辨识精度有一定误差。文献［15］提出了基于内模控制（In⁃ternal Model Control，IMC）的电流解耦策略，解耦效果比较好，在线调节参数少，对参数变化的敏感度小。但IMC需要被控对象的内部模型，当模型失配时，控制效果变差，甚至导致系统不稳。文献［16］提出PI 动态解耦策略，是在电流PI 调节器基础上增加了两个交叉耦合PI 调节器。但是为了使电流很好地跟随，电流环的比例系数就要设置得比较大，从而导致超调较大，影响稳定性。

针对上述问题，本文从实际工程中对控制精度的要求和提高整个系统对电感参数变化的鲁棒性两方面出发，提出基于模型参考自适应和神经网络的电感辨识算法，将神经网络引入到模型参考自适应模型中，即参数辨识的过程就是神经网络的学习过程，不用提前离线训练。该方法简单易实现，解决了由于磁路饱和引起的电感变化问题。建立基于电感辨识的的电机弱磁控制模型，对提出的电感辨识方法进行仿真分析，验证方法的正确性。

2 IPMSM数学模型及弱磁控制

2.1 IPMSM数学模型

IPMSM在d-q坐标系下的电压数学模型为

电磁转矩方程为

式中，ud、uq分别为d、q 轴电压；id、iq分别为d、q轴电压；Ld、Lq分别为d、q 轴电压；Rs为定子电阻；ωe为转子电角速度；ψf为永磁体磁链；p 为电机极对数。

2.2 电机弱磁控制理论

逆变器驱动的永磁同步电机，在满足一定的逆变器电压、电流限制的条件下，通过减弱电机磁场使电机运行与额定转速之上的控制方为即为弱磁控制。由于电机的端电压和电机转速成正比，当电机达到额定转速时，电机的端电压也会达到额定值，此时如果想继续增加转速，就需要减弱励磁磁场来满足电压限制的要求。

永磁同步电机在稳态运行时，电枢电流和端电压需要满足以下条件：

式中，Imax为电机允许运行的最大电流，Umax为电机额定电压，其值取决于直流侧电压值。

若不考虑电机定子电阻压降，将式（1）、（2）代入式（4），并整理变形，有

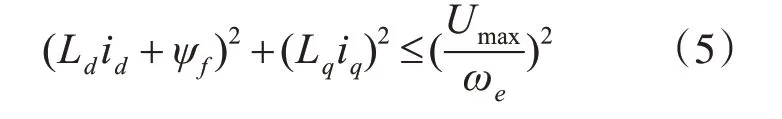
由式（5）可以看出，对于内置式永磁同步电机，由于Ld≠Lq，其电压轨迹是以(-ψf/Ld，0)为中心的椭圆。不同转速下的电压、电流轨迹图如图1 所示。要使实际电流跟踪上给定值，给定电流必须同时处于电流极限圆和电压极限椭圆内。

2.3 电机弱磁控制策略

本文采用定子电流的最优控制策略，在基速以下时，不需弱磁，采用MTPA 控制策略，即图1 中的OA 段，当电压达到逆变器最大电压时，需弱磁运行，沿AD 段运行，此时电压电流均运行于最大值，为弱磁的第一阶段，当转速继续升高，电压极限椭圆与交轴相切时，此时电流控制轨迹为电压极限椭圆在第二象限右边的轨迹，保证了在输出相同转矩情况下，定子电流较小，此时为弱磁的第二阶段，运行轨迹为DE段。

图1 电流控制轨迹

可以看出，d、q 轴电流的精确控制和准确跟踪，对电机转矩的输出、弱磁区的动态特性分析具有重要意义。

3 电感参数辨识算法

基于神经网络的MRAS 的结构图如图2 所示，由图2 可知，改进的辨识系统使用了双层结构ANN 来代替MRAS 的可调模型，用权值调整来取代自适应机构，也就是用误差反传算法替代比例积分自适应，该方法使得参数辨识更加快速，且系统对IPMSM 参数在线辨识的过程便是神经网络的学习过程，不用提前离线训练。

图2 运用ANN的MRAS的框图

3.1 模型参考自适应系统

内置式永磁电机的定子电流模型为

估计得电流变化率可表示为

式中，T 为采样时间。

将式（6）代入式（7），并整理变形，有

用第( k-1) 次采样数据，可得

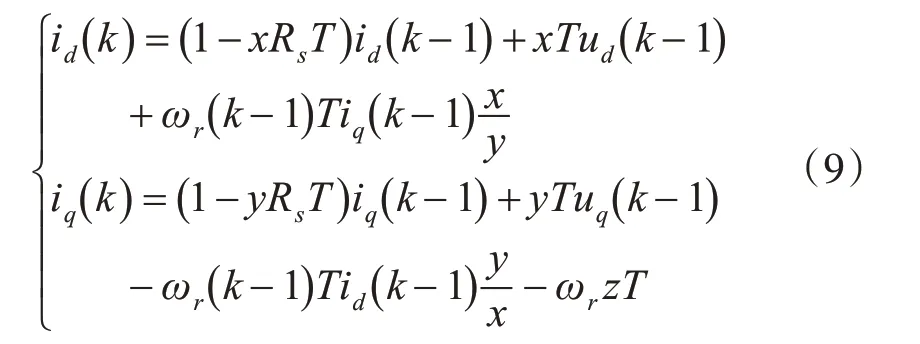
式中，id( k-1) 、iq( k-1) 、ud( k-1) 、uq( k-1) 、ωr( k-1) 为IPMSM 在( k-1) 时刻的值，所以用式（9）作为目标方程，则该式可改写为

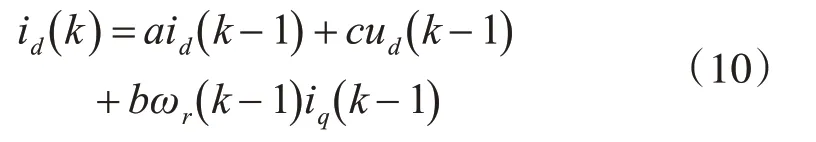
3.2 BP神经网络

针对电感辨识的精度以及辨识速度的要求，将神经网络中隐含层个数设为三个，所采用的传递函数为非线性变换函数—Sigmoid函数，即

选择目标函数：

将以上误差定义式展开至隐含层，有

进一步展开至输入层，有

记xi为输入层至隐含层的输入；yi为隐含层至输出层的输入；ωi为输入层至隐含层之间的权值；vi为隐含层至输出层之间的权值，同时记三层隐含层输出分别为φ1、φ2、φ3。

辨识部分采用的是误差反传算法，即从隐含层输出和输出层输出开始计算，控制流程如图3所示。

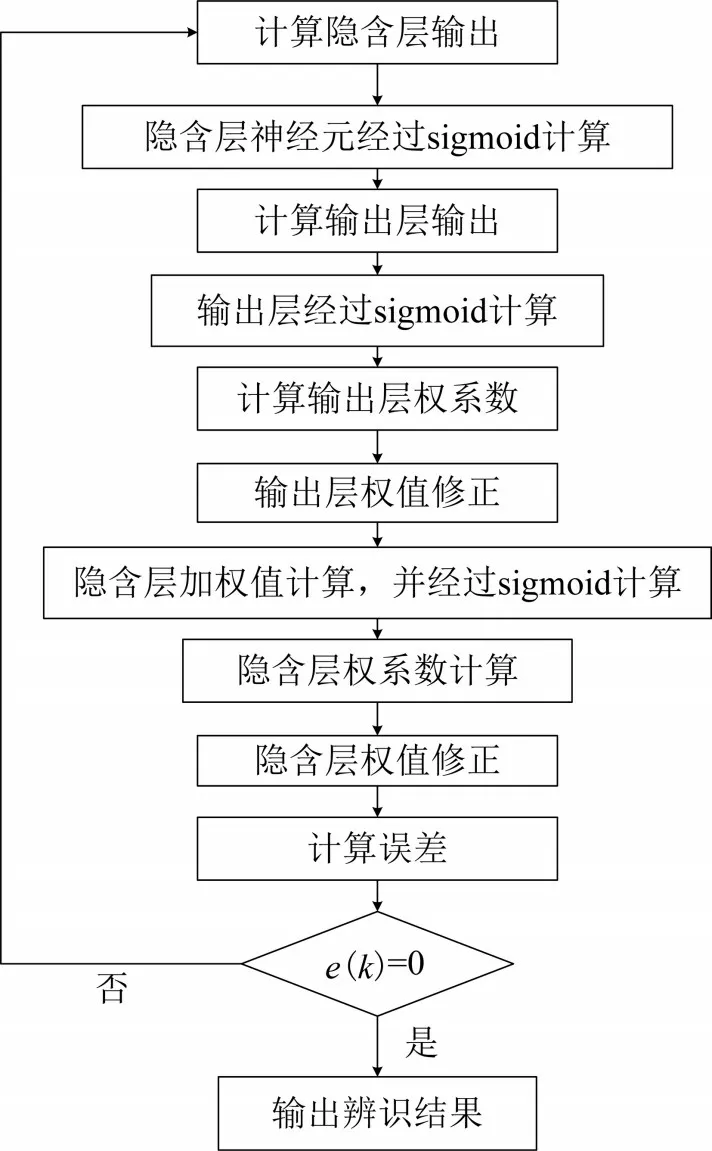
图3 参数辨识流程图

由式（15）可以看出，网络的输入误差是各层权值的函数，因此这里通过调整权值来减小误差，从而进行参数辨识，当e( k )=0 时，辨识过程结束。即应使得权值与误差的梯度下降成正比。引入变量δ1、δ2分别作为隐含层与输出层负梯度下降法的调节系数。为抑制辨识过程中输出结果震荡，引入惯性系数α，此时隐含层与输入层权值的调整公式可整定为

式中，η 为该神经网络的隐含层和输出层的学习效率。以下简述δ1，δ2的推导过程。

记隐含层输出为

输出层输出为

令输出层梯度下降法权系数

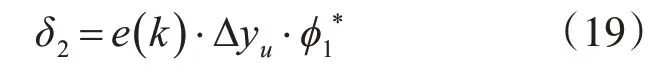
式中，Δyu为权值计算系数，φ1*为隐含层输出加权值计算的第一部分。

定义权值调整系数：

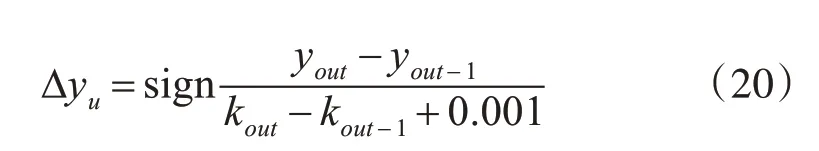
式中，yout为被控对象的输出值；kout为神经网络的输出值。

被控对象的输出值为

记第二层隐含层输出φ2=f(φ1) ，考虑到输出层权系数及输出层权值的影响，有

在参数辨识的过程中，通过电流误差不断的修正神经网络的权值，如果辨识的参数âb̂ĉ与实际的参数abc 相同的时候，则d 轴电流误差应该为零，此时的权值调整完毕，参数辨识工作完成。

4 仿真结果与分析

为验证本文所提出基于模型参考自适应的神经网络辨识算法的有效性，利用Matlab 中的Simu⁃link 搭建用于辨识电感参数的基于模型参考自适应的神经网络算法的模型，并进行仿真。电机参数如表1所示。

表1 电机参数

应用Simulink 搭建用于辨识电感参数的基于模型参考自适应的神经网络算法的模型，其弱磁控制框图如图3所示。

并将其作为一个模块嵌入整个矢量控制系统的系统仿真模型中，函数的输入为电机输出的id、iq、ud、uq、ωr，待辨识参数abc 的学习效率分别为ηa=0.2，ηb=3e-6，ηc=12e-5，惯性系数分别为αa=0.8，αb=0.9 ，αc=0.99 ，仿真用时设定为0.1s，Ld、Lq初始值分别为0.45mH、1.35mH。仿真电感辨识结果如图4 所示。

图3 弱磁控制框图

图4 电机电感辨识结果

由图4 可以看出，本文采用的算法可快速辨识出电感参数，其中d 轴电感辨识时间为0.018s，q 轴电感辨识时间为0.012s，且辨识结果比较准确。由此可以看出，用基于模型参考自适应的神经网络算法对电感参数进行辨识，效果比较理想、实现简单、能够实现参数的实时在线辨识，从而为整个系统所用。

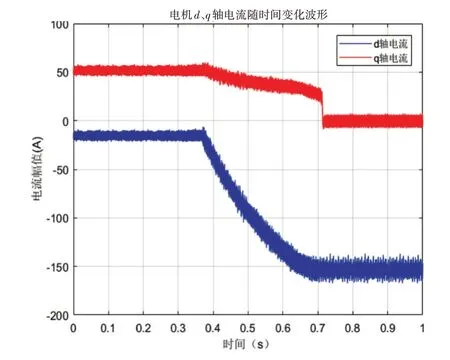
图5 d-q轴电感输出结果

图6 电机转矩输出结果

为验证本文参数辨识算法应用于弱磁控制中的可行性，将上述电感模块的实时辨识结果传递给弱磁控制系统，进行系统仿真。仿真过程设定电机在全速范围内运行，并对比dq 轴电流的跟踪情况及转矩输出能力。

设定仿真时间为1s，电机负载转矩为10Nm，转速给定值设为7000r/min，图5 和图6 分别为未采用电感辨识和采用电感辨识的仿真结果。

从图5 和图6 可以看出，电机在基速以下（0.38s 之前）时，id，iq实际值可以较好跟踪给定值，此时两者交直轴电流输出基本一致；当电机在基速以上（0.38s 之后）时，可以看出图6 较图5 来说，id，iq实际值可以更好地跟踪给定值，即响应时间较快，同时也反映出高速运行时传统控制策略中电流跟踪不准确的问题。

图7 d-q电流轴输出结果

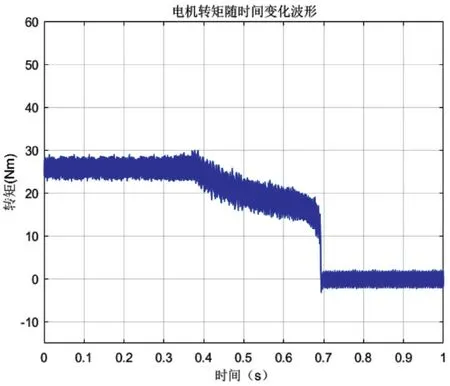
图8 电机转矩输出结果

电流实际值id，iq在弱磁高速区不能准确跟踪给定值，影响了电机转矩的准确输出，在图6中得以体现。由图8可知，加入电感参数辨识后，输出转矩更准确、系统响应更快、到达稳态的时间更短。综上所述，本文提出的辨识算法有效可行，能够达到预期的效果。

5 结语

本文针对电机在高速运行时由于存在交直轴电流耦合，并导致交、直轴电感发生改变，从而影响电机控制效果的问题，提出了基于模型参考自适应的神经网络的电感参数辨识算法。该算法可准确快速地在线辨识出电感参数，消除了高速运行时电流的跟踪误差，提高了转矩输出能力，加快了系统的动态调节过程，提高了系统对电感参数扰动的鲁棒性。