基于小波边缘检测的接地网拓扑成像*

黄明祥

（国网福建经济技术研究院 福州 350012）

1 引言

作为变电站接地系统中最重要的部分，接地网通过平衡地面电压分布和将故障电流输入土壤，为操作员和电气设备提供持续保护。接地网主要由焊接裸钢（或铜）导体制成，这导致易受腐蚀或其他因素导致接地网络功能状态不良。因此，评估腐蚀程度或找出接地网的断点至关重要［1～2］。

用于估计接地网结构状态的常见方法分为两大类：基于电磁场理论的方法和基于电路理论的方法［3］。基于电磁场理论的方法通常测量地面上的电磁场，以确定接地网的状态。表面磁场的分布特征用于检测断点。所建立的电磁场方程一个主要问题在于可能难以避免病态和不稳定的解。基于电路理论的方法利用不同电参数对之间的非线性关系方程来判断是否存在断电。该类方法必须事先了解接地网的拓扑。然而在实际项目中，由于变电站的建设延伸或改建，通常缺少接地网的图纸。

文献［4］设计了一种从地面磁感应的分布特征检测接地网的网格结构的测量系统。该研究采用磁感应的一阶和三阶导数用于拓扑测量。然而，由于土壤分布不均以及泄漏电流的干扰，测量数据中的误差较大，从而导致测量结果不具备工程实用性。为此本文提出将小波边缘检测引入电磁法的接地网检测的思路。小波边缘检测能够通过提取不同尺度的边缘信息，通过综合分析每层的特征充分提取观测数据中有用信息并去除测量噪声的常用工具［5～7］。本文首先讨论接地导体产生的磁场的特性及其梯度，然后详细给出了小波边缘检测在成像拓扑中的适用性和实现。最后通过仿真实验和实地测试证明该方法的可靠性和准确性。

2 成像方法

2.1 接地导体的磁感应特性

为了映射接地网的拓扑结构，需要确定构成接地网的每个导体的确切位置。由于接地导体横截面的等效半径与埋深相比较小，并且其等效直径远小于接地网格间距，因此本文用无限长度的线电流源被用作载流导体的理想模型以表征接地导体产生的磁场［8～9］。

图1 给出了无限长度线电流源的磁感应发布图。图中地面在Z 轴上的位置是：z=hm。如图1 所示，与y 轴重合并向下流动承载电流I 的无限长度线电流源埋在地面下方。假设单层土壤地面具有均匀的渗透率μ。基于Biot-Savart 定律，地面上任意点P（x，0，h）的磁感应强度可表示为［10～11］：

其中r是点P 和导体之间的垂直距离。单位矢量eP与BP的方向相同。由于r2=x2+h2，因此磁感应的垂直分量BZ可以描述为

图1 y轴上无限长度导体电流源产生的磁感应

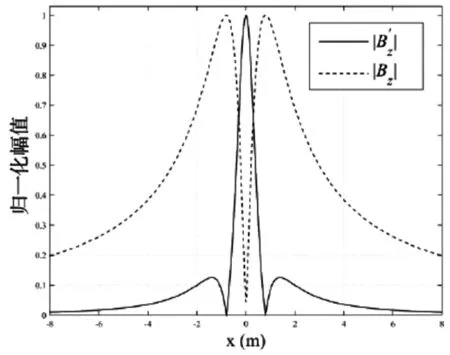
图2 | BZ |和梯度模数 | B′Z |的归一化分布

已有的实验结果表明，直接使用测得的 | BZ|定位接地网，其定位精度较差，并且容易出现错误定位的结果。此外，几乎不可能使用BZ的过零点或|BZ|的最小值来定位接地导体，因为测量的磁感应被表示为来自所有相邻导体的叠加贡献。而变电站中的复杂电磁干扰和土壤中的杂散电流也会引起较大的测量误差［12～13］。

磁感应的垂直分量BZ具有以下明显特征。例如，BZ的最大变化发生在x=0m 处的导体正上方。梯度模量在垂直方向上远离导体衰减，并在x=±h m 的范围内收敛到零。也就是说，由相邻的平行导体引起的磁场对彼此之上的磁场的梯度模量几乎没有变化。如果接地导体通过| B′Z|定位，则可以忽略相邻平行导体的相互影响，因为| B′Z|的影响范围的一半比接地网格间距小两倍。因此，通过在测量数据中找到具有局部最大梯度模数的点来对接地网格的拓扑进行成像将是非常有效的。下面本文利用离散小波变换（DWT）进行边缘检测，计算BZ的梯度。

2.2 小波边缘检测

相对于常用的提取梯度信息的算法，小波变换方法能够有效避免衍生，因此对噪声具有良好鲁棒性并且能够输出相对稳定的检测结果［14］。

比例为2j的二元小波，其中j＞0 且j∈Z，b 的移位可表示为

离散小波变换的f ∈L2( R )通过使用扩张的小波对f卷积来定义：

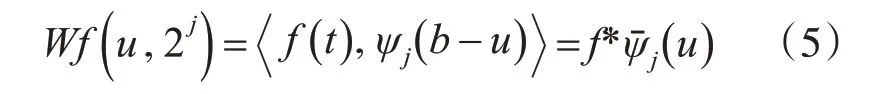
其中：

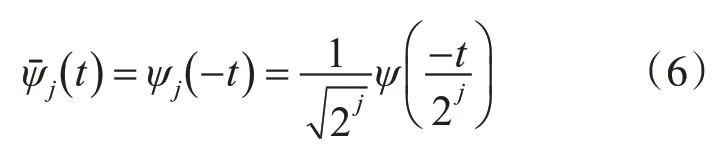
2D 离散小波变换的f( u，v )∈L2( R2)可以通过对两个维度执行一维分裂算法来实现。两个维度的小波定义为

二维离散小波变换的方程为

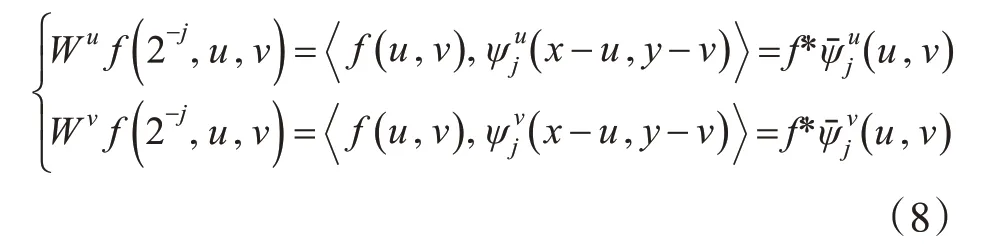
其中：

小波变换的模数与用Canny 算法计算的梯度向量的模数成比例。小波变换的模数可以通过下式计算得出：

2.3 多孔算法

每个小波平面包含小波系数。系数的幅度定义了局部变化的大小，这对于局部特征的提取是重要的。相对于其他小波变换算法（如Mallat 算法），多孔算法可在没有子采样的情况下执行，因此，小波平面和输入数据相同的维度［15～16］。由于多孔算法的平移不变性，在执行边缘检测时避免了额外的误差，并获得了更好的空间质量和冗余信息，这有助于保证接地导体的定位精度。

多孔算法是一种滤波器组方法，使得边缘检测小波被实现为二维可分离小波变换。图3 给出了一维算法的示例。小波变换将尺度为j的近似平面aj( k )分解为新的近似平面aj+1( k )和小波平面dj( k )。多孔算法通过在刻度2j处的每对滤波器系数之间插入2j-1个零来拉伸有限滤波器，而非抽取输入数据。图3 中滤波器组的Z 变换通过将j-1 零点插入值为j的滤波器系数之间来表示拉伸过程。

图3 一维多孔算法

设h（n）是数字低通滤波器，g（n）是由小波的平滑函数构造的数字高通滤波器。设a0(n，m )是二维离散输入，其中∀( n，m)∈Z2。多孔算法的工作原理如下。

对 于 任 何j＞0，aj( n，m )是 系 数2j的 近 似。( n，m )处的DWT系数：

δ={ }δ 是一个离散狄克拉函数，其中δ0=1 和δn={δn=0|n ≠0} 。通过级联0＜j ≤J的卷积来计算二维多孔算法，如下式所示：

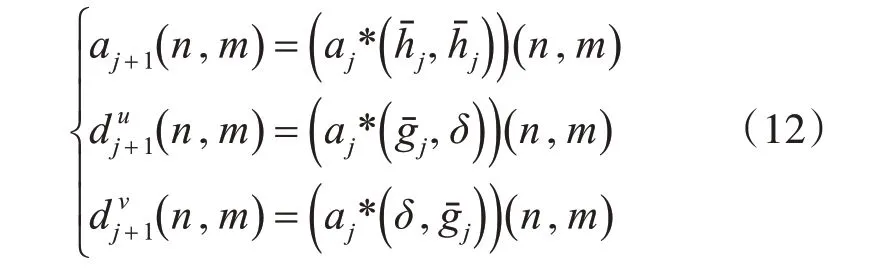
其中：

aj( n，m )沿u 方向和v 方向依次进行低通滤波以获得aj+1( n，m )，该aj+1( n，m )是2j+1的近似值。是aj( n，m )分别沿u 和v 的高通滤波结果。本文采用二次曲线的平滑函数，相应的滤波器是 g( n )=[- 0.5 0.5] 和h( n )=[0 .125 0.375 0.375 0.125] 。

2.4 接地网拓扑成像

所提出的接地网拓扑成像方法可以通过以下过程描述。1）通过可接近的节点将特定频率的正弦电流注入接地网，测量接地表面的磁感应的垂直分量。2）通过移动最小二乘法来重建磁场，并使用规则的离散网格将数据投影到平面上。将网格点与测量区域的实际坐标进行匹配。3）将多孔算法应用于预处理数据。为了改善对比度，对处理后的数据进行低通滤波，以消除DWT 模数中的纹波以进行额外的边缘锐化。4）对接地网的拓扑结构进行成像，确定各接地导体的坐标。

3 仿真和实验验证

3.1 仿真验证

通过仿真和实验结果验证了本文提出的DWT边缘检测方法的有效性。仿真模型采用相对较小的网格间距设计，以使相邻导体的影响最大化。

在COMSOL Multiphysics 5.2a［16］仿真环境下建立了如图4（a）所示的网格尺寸为3m×3m 正方形接地网络模型，采用以原点为中心的15m×15m×6m方盒模拟了被地表（z=0m）等量切割成两部分的计算区域。下部和上部分别是土壤和空气。假设土壤电阻率为50Ω/m，渗透率μ0与真空相同。接地网埋在地表下0.8m，由9个长度为0.9m的垂直接地导线（可接入节点）组成。接地导体采用电阻率为1.38×106Ω·m 钢材料。接地导体的横截面为60mm×6mm。

图4（b）显示了接地网络的顶视图，中心为（0，0，0.8m）。计算过程通过交流/直流模块中的电流接口（ec）和磁场接口（mf）进行。频域（f = 30kHz）求解器配置为使用ec 计算土壤中的电流密度和接地网络。该配置显示注入节点A 并从节点B 流出的3A 电流。求解器使用ec 的结果作为mf 接口的外部输入（电流密度）来计算磁场。地面上8m×8m测量区域的中心位于坐标原点。

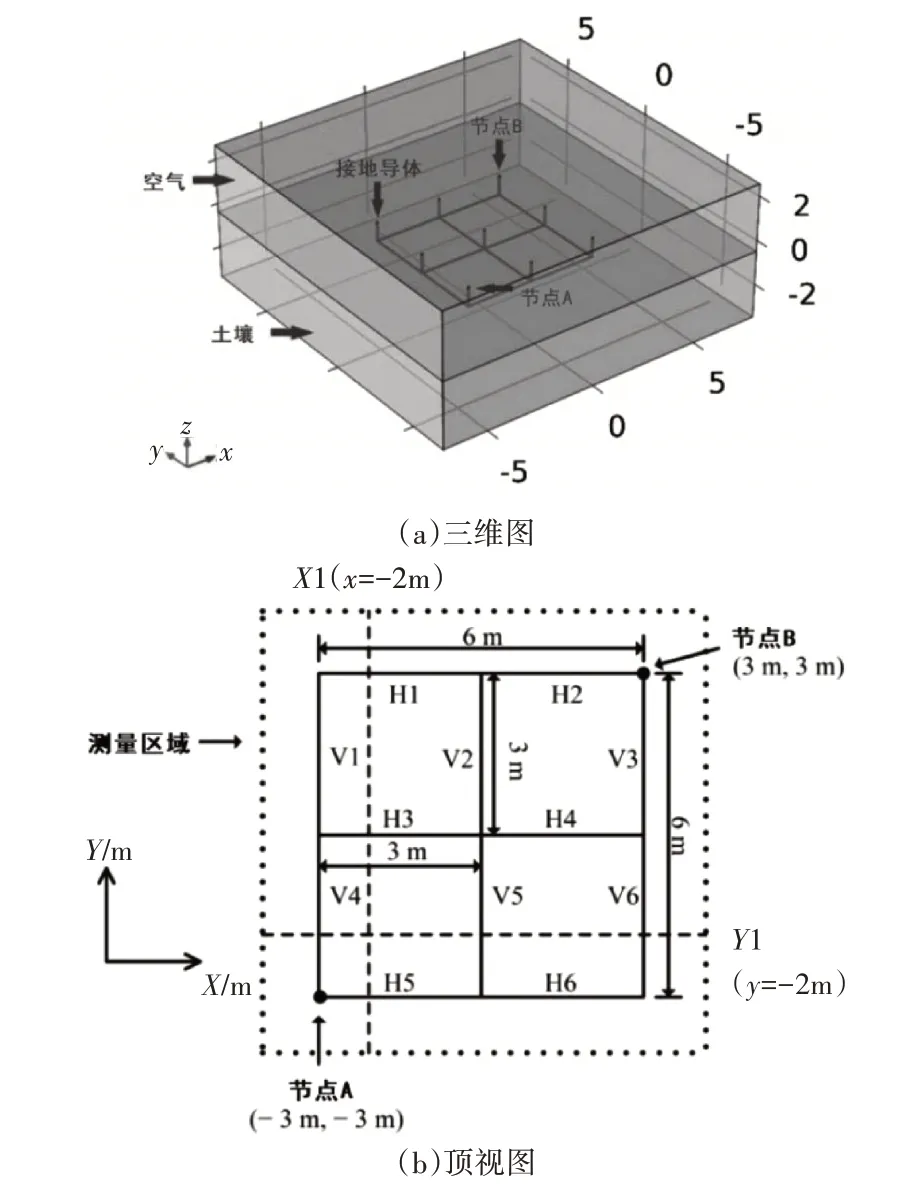
图4 仿真接地网模型

图5 （a）和（b）分别显示了没有边缘检测和有边缘检测的地面上的垂直磁感应结果的等高线图。从图5（a）可以看出，测量结果都处于模糊状态，不太可能提取有关接地网拓扑的有用信息。相比之下，图5（b）显示了可辨别的接地网拓扑结构。该结果表明，所提出的小波边缘检测方法使图像能够产生可视化的拓扑信息，并有助于以高分辨率定位导体。可以通过识别DWT 的局部最大模数来提取导体的位置。在图6 中示出了在x=-2m 处的两个轮廓X1 上的特征和在y =-2m 处的Y1（参见图4）。测量结果如表1 所示。由表1 数据可知，最大绝对误差是1.2cm，这与接地网导体间距3m相比非常小。

图5 地面磁感应垂直分量的仿真结果

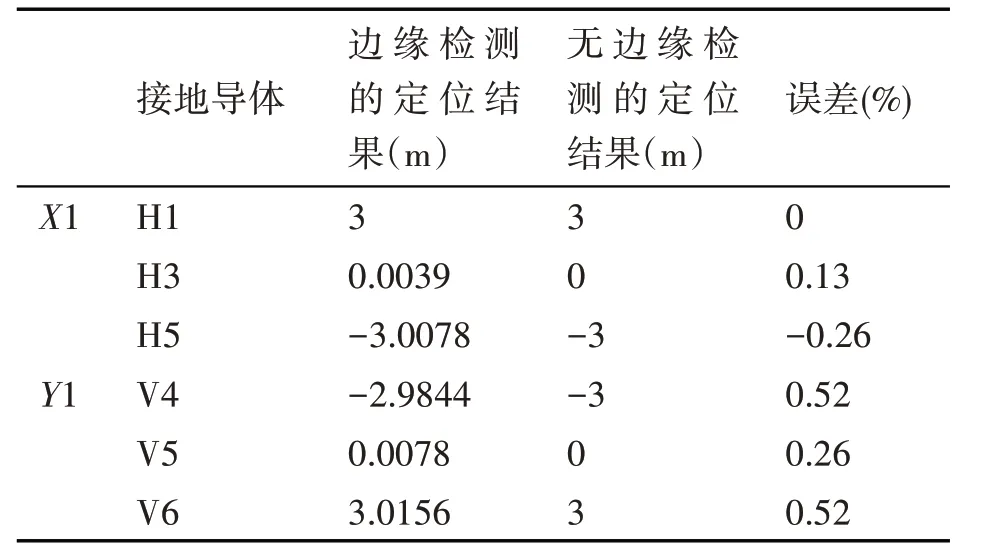
表1 仿真结果

所示方法对损坏的接地导体的检测性能如图6所示。假设V5是损坏的接地导体。对于V5未完全破坏的情况，损伤程度通过电阻值变化来量化。 假设V5 的正常电阻为N Ω。通过收缩V5 的横截面，其电阻值增加到2N、5N 和10N。仿真实验中V5 的损坏时通过在V5 中间设置1cm 宽的断点来模拟的。

图6 接地导体V5受到不同程度的损坏的电阻值变化

从图6 中可以看出，当V5 轻微损坏时，电阻从NΩ增至5NΩ的电阻，所提方法的检测性能几乎不受影响。然而，当V5严重损坏或损坏时，边缘检测性能严重下降，因为导体V5 上几乎没有任何电流来凸显梯度特征。但是在这种情况下如果已知接地网的实际拓扑结构，所提方法的检测结果能够用于检测接地导体的损坏或严重腐蚀程度。

3.2 实验验证

实验接地网设置如图7所示，其中所设置的2×2 平方接地网位于地表下0.45m 处。每个接地网格的尺寸为2.06m×2.06m。为了检验可靠性，本文引入了以下一些设置来验证所提方法在不同情况下的检测性能。首先，使用直径为0.52mm 的细铁丝来构建接地网。线越细，位置检测所需的分辨率越高。其次，土壤被抑制以增加泄漏电流的影响，这可能导致不良结果。最后，将少量33kHz、约0.23A的电流注入节点A并流出节点B。

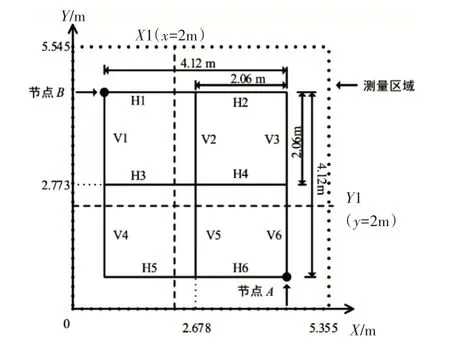
图7 实验接地网和测量区域的详细信息

使用300匝圆形空芯线圈测量图7所示测量区域的磁感应垂直分量。线圈采用0.19mm半径的漆包线缠绕，线圈半径为0.098m 使用IOtech Model 650u 数字信号分析仪，通过在LabVIEW 上编写的定制控制面板上运行的笔记本电脑，对受控制的磁场进行数字化和记录。笔记本电脑和信号分析仪之间的通信是通过USB2.0接口进行的。每条测量线之间的间距在0.325m 和0.225m 之间交替，而每个点之间的间距固定在0.255m。用平行于水平方向的20条测量线进行实验。每条测量线包含22个点。移动线圈以记录所有位置的数据，并收集每个点的数据2s。测量区域的尺寸为5.355m×5.545m，接地网的中心位于（2.678m，2.773m）。

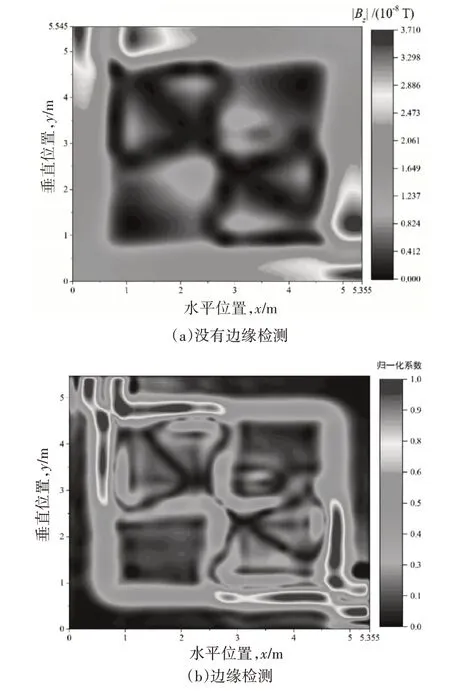
图8 地面磁感应垂直分量的实验结果

图8 （a）给出了在地面上测量的垂直磁感应的等高线图，图8（b）给了使用所提出的边缘检测方法的改进结果。与模拟结果相比，DWT 的混沌分布发生在导体接头周围的区域。

首先，在接地导体接头处发生严重的电流泄漏。在接头周围的区域中，泄流电流触发更多的杂散电流，这对边缘检测的质量具有负面影响。在仿真实验中电流泄漏均匀分布在模拟均匀土壤中，然而，在实际应用因为土壤密度不均匀导致更复杂的情况。实验结果表明，在接地网内部的四个导体（H3，H4，V2 和V5）中流动的电流通常小于其他导体中的电流。在考虑接地网的频率响应时，需要考虑这种现象。

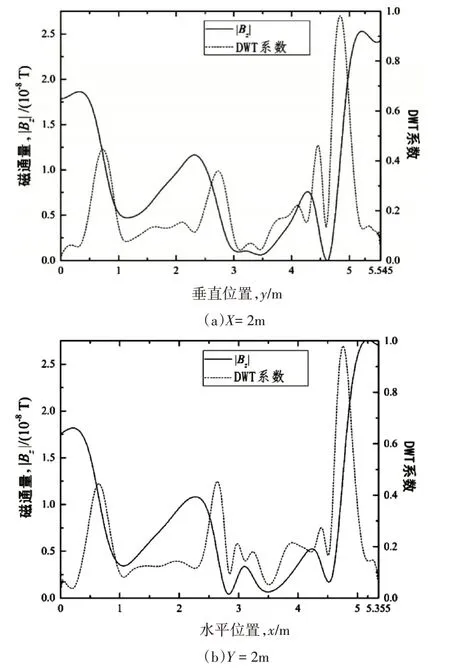
图9 两个接地导体的磁同类和DWT系数

表2 实验结果

从图8（b）可以看出，虽然细节在接地导体周围仍然是模糊的，但是能够分辨出2×2 网格的拓扑结构。选择x=2m 处的X1 和y=2m 处的Y1 两个接地网轮廓进行测量所得出的磁通强度和DWT 系数如图9（a）和（b）所示。通过在三个可能区域中找到DWT 系数的局部最大值来提取每个轮廓上的三个导体的位置。例如，在轮廓X1 上，在y = 0.73m、2.73m 和4.85m 处出现三个DWT 峰值，分别代表三个导体H5、H3和H1的位置。表2将实验结果与轮廓X1 和Y1 的理论值进行比较。通过对多个平行轮廓求平均值，可以减小实验和理论结果之间的差异。

4 结语

本文提出了一种基于小波边缘检测的接地网拓扑检测方法。仿真和实验结果表明，该方法可以准确定位接地网导体。此外，该方法可以在连续测量中操作而不会中断停电或土壤挖掘。为了提高检测结果，建议使用具有高电流幅度和功率的电源。 更高的功率引起更大的测量磁感应，这可以增强边缘检测的重要性。此外，从多个节点进入接地网的多点注入电流也可以改善电流分布以及成像质量。