基于改进的隐马尔可夫模型的新闻推荐算法*

张 丹 周从华

（江苏大学计算机科学与通信工程学院 镇江 212013）

1 引言

随着移动设备的日益普及和互联网的迅猛发展，人们越来越习惯于通过电脑或智能手机阅读新闻。各种新闻网站为用户提供在线新闻服务，但是面对成千上万篇新闻可供选择，人们很难快速地从中找到自己下一时刻将要阅读的新闻。这时新闻推荐系统应运而生。

传统的新闻推荐算法通常是分别对用户和新闻建立模型，再进行相似度计算，然后进行匹配排序，将用户有可能感兴趣的新闻按兴趣值从大到小推荐给他。可是传统的新闻推荐算法有着数据稀疏以及冷启动问题。过去有些学者将时间特征融合到新闻推荐算法中［1～2］。以此来证明用户的兴趣是随着时间的推移而改变的。但是，很少有人考虑到时间序列特征，而用户阅读新闻时一般是以时间序列的形式［3］，文献中提出了一种基于改进的协同过滤时间序列推荐算法，在协同过滤算法中考虑时间序列，但是它不可避免地也有着协同过滤中的数据稀疏性和冷启动问题。隐马尔可夫模型主要用于处理时间序列特征，即样本之间有时间序列关系的数据，所以本文利用隐马尔可夫模型来着重预测用户在特定新闻之后将要阅读的下一篇新闻，用户下一篇将要阅读的新闻只与当前阅读的新闻有关，与之前的行为都无关。这样就有效缓解了数据稀疏和冷启动问题。在此基础上，本文引入了状态驻留时间元素，来表明在此状态中停留的时长，提高了推荐的准确度。

2 相关工作

推荐算法主要分为基于协同过滤的推荐算法和基于内容的推荐算法，而基于协同过滤的推荐算法里又分为基于用户的协同过滤和基于项目的协同过滤。新闻推荐算法中更常用的是基于用户的协同过滤和基于内容的推荐。

基于用户的协同过滤是根据用户阅读过的新闻而找出同样阅读过这些新闻的用户，也就是目标用户的邻居用户，从而证明这些用户与目标用户在一定程度上是相似的，再将这些用户阅读过而目标用户没有阅读过的新闻推荐给目标用户。

基于内容的推荐是将用户阅读过的新闻进行特征提取，新闻中一般采用的是TF-IDF模型，然后将与这个内容相似的新闻推荐给用户。

但是这些算法都有着一些问题，例如文本处理较复杂，增加了算法的复杂性；还有数据稀疏和冷启动问题。

新闻推荐网站中较有名的如Google。在Google新闻中，对已经登录并明确启用网络历史记录的用户，推荐系统会根据用户的过去点击行为构建用户新闻兴趣，使用贝叶斯算法来预测用户对当前新闻的兴趣［4］。本文着重根据当前阅读的新闻，去预测下一篇可能阅读的新闻，也就是说将当前阅读的新闻和将要阅读的新闻视为上下文关系。有人曾根据用户的上下文信息和新闻内容，主动向移动用户推送即时个性化新闻［5］。

隐马尔可夫模型是一个关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态序列，再由各个状态随机生成一个观测而产生观测序列的过程。我们常将隐马尔可夫模型应用到语音识别、输入法、地图匹配、金融预测、DNA序列分析等。

文献［6］中用隐马尔可夫模型去预测用户的评分轨迹并结合BP神经网络进行用户的偏好学习最终产生推荐结果。但是它没有考虑到在隐马尔可夫模型中，模型在某状态停留一定时间的概率是随着时间的增长呈指数下降的趋势的，所以传统的隐马尔可夫模型并不能合适的表征用户评分轨迹的时域结构。

3 基于改进的隐马尔可夫模型的新闻推荐算法

3.1 隐马尔可夫模型

隐马尔可夫模型（Hidden Mar kov Model，HMM）属于动态的贝叶斯网——一种有向图模型。隐马尔可夫模型中的变量分为状态变量和观测变量。状态变量｛y1，y2，…，yn｝，其中yi∈Y 表示第i时刻的系统状态。状态变量我们一般认为是隐藏的，不能被观测到的，所以我们又称它为隐变量；观测变量｛x1，x2，…，xn｝，其中xi∈X 表示第i时刻的观测值。在隐马尔可夫模型中，系统一般在多个状态｛s1，s2，…，sN｝中转换，所以状态变量yi的取值范围Y（称为状态空间）通常是有N 个可能取值的离散空间。并假定观测变量xi的取值范围X 为｛o1，o2，…，oM｝。无论何时，观测变量的取值依赖且仅依赖于状态变量，即xt由yt确定，与其他状态变量及观测变量的取值无关。同时，t 时刻的状态yt依赖且仅依赖于t-1 时刻的状态yt-1，与其余的n-2 个状态无关。这就是所谓的“马尔可夫链”（Markov chain），也就是说：系统下一时刻的状态仅由当前状态决定，不依赖于以往的任何状态，基于这种依赖关系，所有变量的联合概率分布为

以上为隐马尔可夫模型的结构信息，除此以外，想要确定一个隐马尔可夫模型还需要一个三组参数。

1）状态转移概率：模型在各个状态之间转换的概率，一般记为矩阵

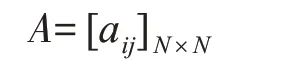
其中aij=P（yt+1=sj|yt=si），1 ≤i，j ≤N 。表示在任何时刻t，若状态为si，则在下一时刻状态为sj的概率。

2）输出观测概率：模型根据当前状态获得各个观测值的概率，一般记为矩阵

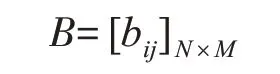
其中：bij=P(xt=oj|yt=si)，1 ≤i ≤N ，1 ≤j ≤M ，表示在任何时刻t，若状态为si，则观测值oj被获取的概率。

3）初始状态概率：模型在初始时刻各状态出现的概率，一般记为

其中πi=P（y1=si），1 ≤i ≤N 。表示模型的初始状态为si的概率。

通过以上可知，一个隐马尔可夫模型的确定，需要状态空间Y 、观测空间X 和三组参数［A，B，π］。一般用参数λ=［Y，X，A，B，π］来表示一个隐马尔可夫模型。给定一个隐马尔可夫模型λ，它根据以下过程可以产生一个观测序列｛x1，x2，…，xn｝：

1）设置t=1，并根据初始状态概率π 选择初始状态y1；

2）根据状态yt和输出观测概率B 选择观测变量取值xt；

3）根据状态yt和状态转移矩阵A 转移模型状态，也就是确定yt+1；

4）若t ＜n，设置t=t+1，并返回第2）步，否则停止。

其 中yt∈{s1，s2，…，sN} 和xt∈{o1，o2，…，oM}分别为第t时刻的状态和观测值。

3.2 基于改进的隐马尔可夫模型的新闻推荐算法

一般的新闻推荐算法没有考虑到用户浏览新闻的时间序列特征。也就是说可以用来预测用户将点击的下一篇新闻，用户对新闻的操作序列正好符合隐马尔可夫随机过程。我们将用户对新闻的操作行为假设为可观测的，被操作的新闻即观测值，操作行为我们分为点击、评论、收藏三种，三者的权重我们暂不考虑。系统对于用户的阅读兴趣是未知的，那么下一次的对新闻的操作行为只与当前的状态有关，与之前的状态无关。

根据上一节的概述将隐马尔可夫模型融合到新闻推荐算法中。再此基础上，我们引入了状态驻留这个概念，在原来5 个元素的基础上加入了驻留时间的元素，在t 时刻对新闻操作行为的状态y 的概率依赖3 个因素：在t-1 时刻的对新闻操作行为的状态yt-1；用户在前一个新闻的驻留时间dt-1；t时刻观测到的新闻序列ot。随着新闻ID 的改变，驻留时间d 重新置0，因此，d 可以表示一个用户对某个新闻进行操作行为的持续时间。

3.2.1 参数初始化

λ=［Y，X，A，B，π，d］进行初始化：

1）Y：状态Y 代表的是用户对新闻操作的可能的取值集合，N表示集合中元素的数量；

2）X：观测值X 代表的是用户可能感兴趣的新闻ID 的集合，表示的是系统可以观察到的用户操作的新闻，M表示集合中元素的数量；

3）A：状态转移概率矩阵A=[aij]N×N，aij=P（yt+1=sj|yt=si）（1 ≤i，j ≤N）代表的是系统中所有用户在t 时刻对新闻的操作行为为si，在t+1 时刻转移到操作行为为sj的概率，这里的t 仅代表操作行为的先后时间顺序。

其中，1 ≤i，j，k ≤N；

4）B：输出的观测值概率分布矩阵B=[bij]N×M，bij=P(xt=oj|yt=si)（1 ≤i ≤N ，1 ≤j ≤M）代表的是用户的操作行为为si)且它正好是新闻ID 为oj的概率。

其中，1 ≤i ≤N ，1 ≤j ≤M ；

5）π：初始状态的概率矩阵π={πi} ，πi=P（y1=si）（1 ≤i ≤N）代表的是系统中所有的用户第一次的操作行为为si的概率。

其中，1 ≤i，j ≤N；

6）d：驻留时间Pi(d) =P（τt=d|yt=si）（1 ≤i≤N）代表的是在t 时刻操作行为状态为si上驻留时间为d的概率。

3.2.2 模型参数学习

根据T 时刻目标用户给出的进行过操作的新闻ID 序列（观测值序列）X={x1，x2，…，xT}和状态序列Y={y1，y2，…，yT} ，采 用 基 于EM 算 法 的Baum-Welch算法进行模型训练，使之不断迭代，并在此过程中更新初始模型，每次迭代都使似然函数P（x| λ）朝着局部最大方向变化，以保证得到该似然函数最大的模型。直接计算P（x| λ）的话，运算量很大，而前向-后向算法可以使之变得简捷高效。

1）前向变量αt（i）：表示在t 时刻处于状态i 的概率，并且假设t+1时刻的状态为j。

可得出：

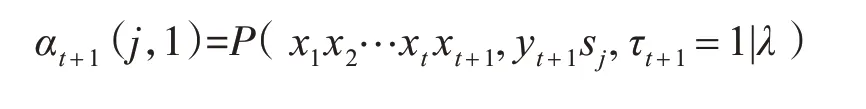
其中，1 ≤j ≤N，1 ≤t ≤T-1；

2）后向变量βt（i）：表示在t 时刻的状态为si，那么从t+1 时刻到T 时刻的观察序列为X=｛xt+1，xt+2，…，xT｝的概率，

可得出：

其中，βT（i，d）=1，1 ≤i ≤N，1 ≤t ≤T-1; 1 ≤d ≤D。

3）求解P（x| λ）

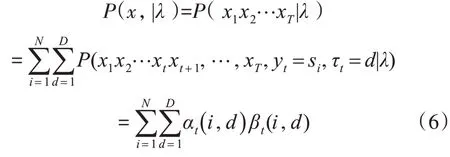
其中，1 ≤i ≤N，1 ≤t ≤T 。

4）假设用户在t时刻对新闻ot的操作行为为si及在此状态的驻留时间为d，并且在t+1 时刻对新闻ot+1的操作行为为sj的概率为γt（i，j，d）（1 ≤i，j ≤N，1 ≤t ≤T）。由式（4）～式（6）可得：

5）假设用户在t时刻对新闻ot的操作行为为si及驻留在此状态的时间为d的概率为δt（i，d）（1 ≤i≤N，1 ≤t ≤T）。

由式（4）～（6）可得：

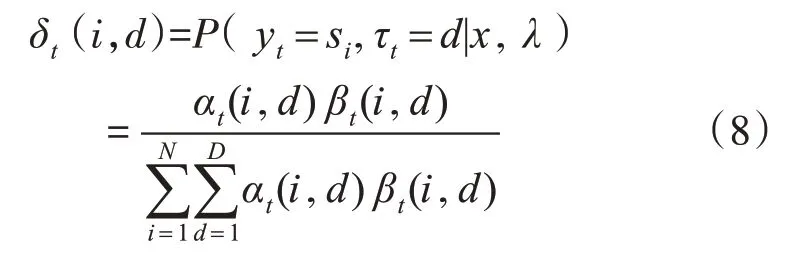
所以：

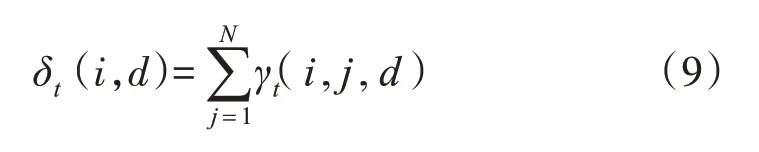
6）由4）和5）可知，用户对新闻的操作行为习惯从si转移到sj的期望为

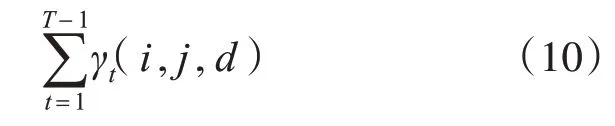
7）更新隐马尔可夫模型参数λ’=（Π′，A′，B′）

当xt=ot时，Cxt，ot=1，否则Cxt，ot=0。

8）重复以上步骤，直到Π′，A′，B′收敛，此时P（x|λ′）最大。

3.2.3 生成推荐列表

通过以上可以得到最优隐马尔可夫模型λ′=（Π′，A′，B′），根据模型λ′和用户的对新闻的历史操作行为路径，计算下一时刻用户可能操作的新闻xT+1，以及对应的操作行为si使得P（x1x2…xTxT+1|λ′）最大，将xT+1加入给用户的推荐列表中，在以上步骤上重复K-1 次，最后生成推荐列表w=

4 实验结果及分析

4.1 实验数据集

在我们的实验中，数据集采用的是某新闻网站的后台新闻日志数据，可在github中查看［7］。对基于隐马尔可夫模型的新闻推荐算法进行模型的训练分析。随机选取了1000名用户的行为记录，如图1所示，包括用户id，新闻id，操作行为时间，新闻标题，操作行为。按照操作行为的时间顺序，前80%为训练集，后20%为测试集。

图1 数据集示例

4.2 评价指标

我们将基于隐马尔可夫模型的新闻推荐算法（HMM）与传统的基于用户的协同过滤推荐算法（User-based CF）和基于项目的协同过滤推荐算法（Item-based CF）进行对比，设Τ 为测试集，ℱ 为推荐结果。本文的性能指标参考准确（Precision，P），召回率（Recall，R）以及F1指数。

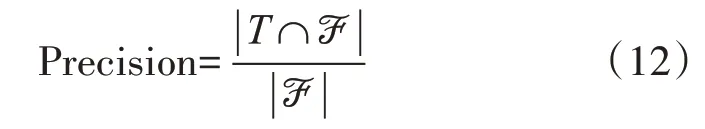
Precision 描述了推荐精度，数值越高意味着更少的用户得到错误的推荐。

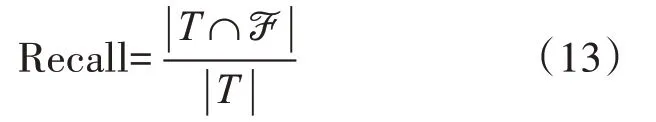
召回率越高意味着越多的用户得到正确的推荐，但这通常是以牺牲精度为代价的，所以为了全面评价三个推荐算法的性能，引入了F1 作为最重要的综合指标之一，F1越高意味着综合性能最好。

我们将三个算法按照时间的变化统计用户的行为数据进行推荐，实验结果如图2 ～图4所示。

图2 准确率随时间变化对比

图3 召回率随时间变化对比

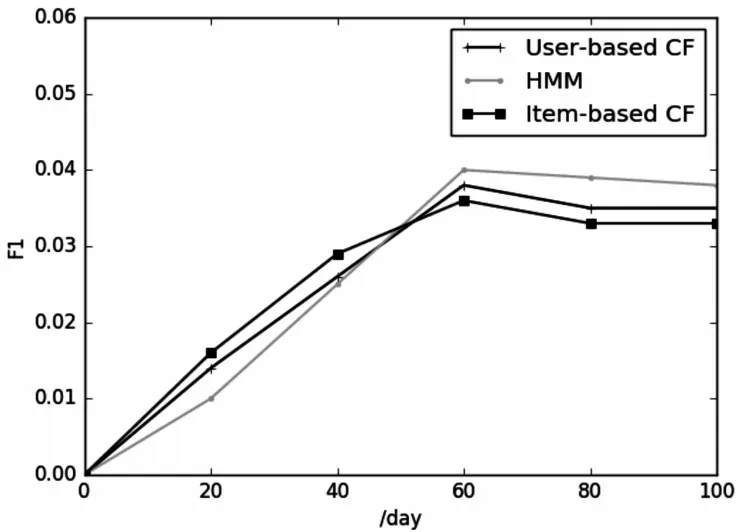
图4 F1指数随时间变化对比

由图2～图4 可知，传统的User-based CF 和Item-based CF 算法的准确度随着时间的推移下滑明显，明显不及HMM 的新闻推荐算法。F1 指数也是随着时间的推移，HMM 的新闻推荐算法后来居上。由此可见，基于隐马尔可夫模型的新闻推荐算法是有效的，推荐性能相比传统的协同过滤得到了提升。

5 结语

传统的新闻推荐算法一般是协同过滤或者基于内容的推荐，这其中对于时间特征的研究都较少，少有的也是对于用户兴趣建模，随着时间的推移，用户兴趣的改变。而用户阅读新闻时是按照时间序列的形式，所以我们着重在预测用户下一篇将要阅读的新闻上也就是找出用户的阅读轨迹。

这对于时间序列的研究与隐马尔可夫模型相吻合，所以我们将隐马尔可夫模型融合到新闻推荐算法中，在此基础上引入状态驻留时间元素来表示用户对该新闻的喜欢程度，提出了一种新型的基于时间序列的新闻推荐算法，用户下一篇将要阅读的新闻只与当前阅读的新闻有关。经过广泛的实验证明，我们提出的新算法具有较高的有效性与可行性。在之后的工作中，我们将进一步完善以及改进算法。