基于灰色关联分析和PSO 改进的多变量GM（1，N）模型*

李克文 李 萍

（中国石油大学计算机与通信工程学院 青岛 266580）

1 引言

长期以来，许多学者对预测理论进行了广泛深入的研究，并提出一系列预测方法，如时间序列法、人工神经网络法、支持向量机法、灰色预测法等［1～2］，这些方法大多采用单变量建模和预测，不能充分考虑变量之间作为整体存在时的相互影响［3］，且在预测过程中需要大量可靠地预测数据作为支撑。随着研究的深入，一些学者提出多变量灰度预测模型，也称为GM（1，N）模型，灰色预测模型是灰色系统理论中最重要的组成部分之一，通过对“部分”已知信息的分析，提取有价值的信息，实现对数据变化规律的正确描述和有效预测［4］。

对灰度预测模型的改进研究一直是近年的热点［5～6］：通过改进初始条件或利用智能算法获取更为合适的背景值［7～8］，从而获取更为准确的预测效果。GM（1，N）模型的结构比单变量灰色预测模型复杂，建模过程充分考虑了相关因素对系统变化的影响［9～10］，但GM（1，N）模型存在建模机制和模型结构上存在不足，因此在实际应用中常常导致模型误差大于GM（1，1）模型。为了提高GM（1，N）模型的仿真和预测性能，Tien 优化了传统GM（1，N）模型的结构，在该领域发挥了重要作用［11］；Wang等通过引入控制参数和插值系数，提出了一种基于卷积积分的GMC（1，N）优化模型［12］；Zeng等提出了一种新的OGM（1，N）模型，解决了传统GM（1，N）模型的建模机理、参数估计和模型结构的缺陷问题［13］。本文在OGM（1，N）基础上，以模型还原值和实际值的误差平方和最小化为目标，提出一种基于灰色关联分析和PSO算法的多元变量灰度预测模型，通过灰色关联度计算获取与参考序列变化密切相关的自变量序列，基于PSO 算法改进模型初始条件，在N = 1 和N ＞1 两种情况下分别对模型进行建模预测和发展系数求解优化，降低模型范围，从而提高了改进模型的预测精度和适用范围。

2 OGM（1，N）模型建模原理

通过研究发现，GM（1，N）模型存在一些严重的缺陷［13］：1）作为一个有N个变量和一个一阶方程的灰色预测模型，当N =1 时，现有的GM（1，N）模型不能转化为相应的GM（1，1）模型，这说明GM（1，N）模型的结构存在一定的缺陷；2）GM（1，N）模型的最终时间响应表达式是通过一个理想的简化过程得到的，这可能会导致GM（1，N）模型的不稳定性；3）参数估计与参数应用的错位是传统GM（1，N）模型的第三个缺陷。针对GM（1，N）模型现有的建模机理、参数估计和模型结构三个方面的严重缺陷，Zeng 等引入线性修正项h1（k-1）和灰色作用量项h2，提出了一种新的灰色优化模型OGM（1，N）［13］，解决了传统GM（1，N）模型的三个缺陷，其建模过程如下：

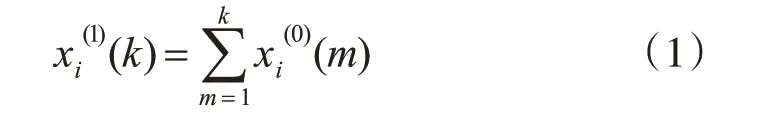
其中i=1，2，…，n，k=1，2，…，p。

2）由Xi（1）生成紧邻均值序列Z（1）＝｛z1（1）（k）｝（k=1，2，3，…，p）。

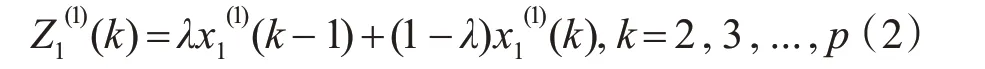
其中，背景值λ 默认为0.5。假定X（1）具有近似指数变化规律，数列X2（1），X3（1），…，Xn（1）对X1（1）的变化率产生影响，则Xi（1）序列满足下述的一阶线性微分方程：

这个微分方程模型记为GM（1，N），将上式离散化，并引入线性修正项h1（k-1）和灰色作用量项h2，得到OGM（1，N）灰微分方程如下：

记式（4）的离散形式如下：

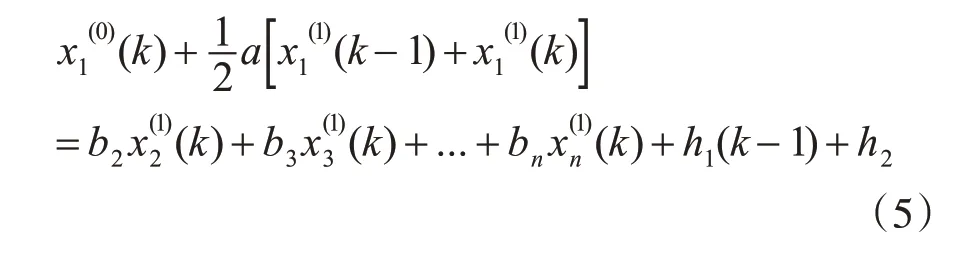
其中，k=2，3，…，p，a 为系统的发展系数，bi为驱动系数，线性校正项h1（k-1）反映了因变量和独立变量之间的线性关系；灰色作用量项h2表示因变量序列中的数据变化关系。要求解此微分方程，须先确定参数a、bi、h1、h2。

3）利用最小二乘法求得参数a、bi、h1、h2的值：

其中：

4）将a、bi、h1、h2的值带入式（5）解微分方程，得其离散解为

其中：

5）对式（7）做一次累减还原运算，得到原始序列X1（0）的灰色预测值：

3 基于灰色关联分析和PSO 对OGM（1，N）模型的改进

本文在OGM（1，N）模型的基础上，通过灰色关联分析法评估各个因素与预测数据的关联程度，从而挖掘出对预测数据影响较大的因素组成自变量序列，作为灰度预测模型的输入，另外，针对OGM（1，N）建模过程中的参数估计问题，利用PSO 算法分别在N=1和N ＞1两种情况下对模型中a、bi、h1、h2值进行求解优化，避免直接定义背景值λ=0.5，再对a，b 值进行求解产生的双重误差，使模型误差最小化。

3.1 基于灰色关联分析的选择

作为比较数据序列，是影响系统行为的因素。

2）确定每个数据序列中的最大值和最小值，针对参考数列和比较数列进行无量纲化处理：

3）计算比较数列xi和参考数列x1在第k个指标上的灰色关联系数：

4）计算灰色关联度γi：

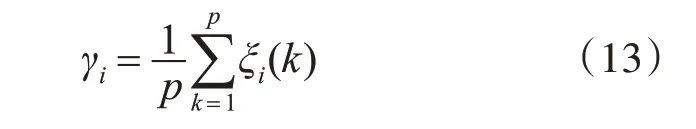
设置关联度阈值γ0=0.6，提取｛γi|γi＞γ0｝的特征属性集组成新的自变量数据序列Xi'（0）=｛xi'（0）（1），xi'（0）（2），…，xi'（0）（p'）｝，i=1，2，…，n，为方便后续表达，将Xi（'0）记为新的X（i0）。

3.2 基于粒子群算法对OGM（1，N）模型的改进

根据变量参数N 的大小，采用粒子群算法对具体参数进行优化求解，最小化模型误差。POGM（1，N）建模过程如下：

2）I.当N = 1 时，令h1=0，将OGM（1，N）模型转换为GM（1，1）模型：

由G（k+1）-G（k）可得：

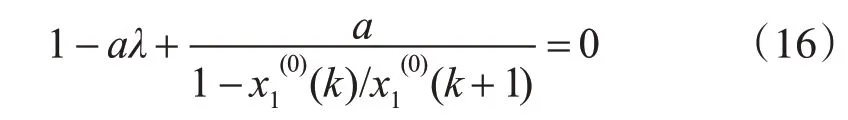
又根据GM（1，1）模型原理可得：

联立式（16）、（19）可得，

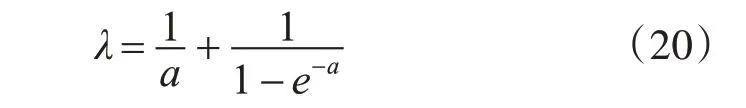
（1）初始化一个规模为m（m ≥4）的粒子群，设定初始位置向量ai=（ai1，ai2，ai3，…，aim），h2i=（h2i1，h2i2，h2i3，…，h2im）和初始速度向量Vi=（vi1，vi2，vi3，…，vim），因为在实际运用过程中a 的取值不会超过0.5［15］，所以：

（2）将a，h2的值代入式（18），求得：

II.当N ＞1时，OGM（1，N）模型如下所示：

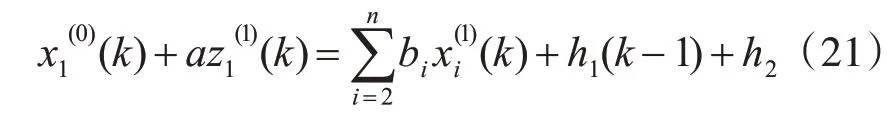
（1）初始化一个规模为m 的粒子群，设定初始位置向量λi=（λi1，λi2，λi3，…，λim）和初始速度向量Vi=（vi1，vi2，vi3，…，vim），每当给定一组li，PSO 调用OGM（1，N）模型文件即可获得一组对应参数解：［b2，b3，…，bn，a，h1，h2］i，根据实际运用过程［15］，参数解须满足以下条件：

（2）将a，bi，h1，h2的值代入式（7）、（8）、（9），求得

3）计算每个粒子的适应度值，取适应度函数为

4）比较每个粒子的适应值fmin和其经历过的个体 最 优 位 置pbest 的 适 应 值fpbest，若fmin＜fpbest则 更 新fpbest=fmin；

5）比较每个粒子的适应值fmin与其经历过的全局最优位置gbest 的适应值fgbest，若fmin＜fgbest则更新fgbest=fmin；

6）在找到这两个极值后，根据粒子的速度、位置进化方程来更新粒子；

7）如果满足终止条件，则输出解，否则返回3）继续循环查找。

4 改进的灰色模型在数据预测中的应用

本文基于文献［13］中的抗拉强度数据集和文献［3］中的基坑监测数据集进行实验分析，具体实验数据如表1、表2所示。在实验数据的基础上，取ρ=0.05，根据3.1 节中的灰色关联分析法分别对表1、表2 数据集的三组数据序列进行灰色关联度计算，计算结果如表3 所示，γ12，γ13均大于0.7（最常用的临界值为0.6），说明三组数据序列之间相互关联，两个数据集均可以作为预测模型的输入。

表1 抗拉强度数据集

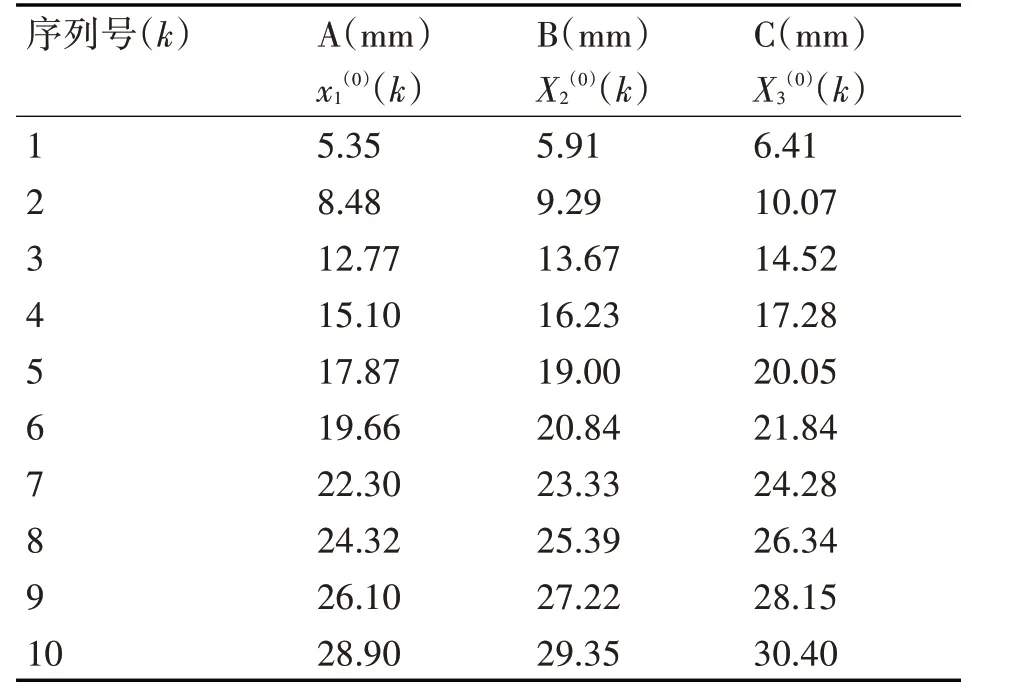
表2 基坑监测数据集

表3 基坑监测数据

为了全面验证POGM（1，N）模型效果的有效性，本文在Matlab 平台上进行实验，分别将表1、表2 数据集的前六个序列根据3.2 节中基于PSO 优化的OGM（1，N）模型（简称为POGM（1，N）模型）、GM（1，1）模型、GM（1，N）模型和OGM（1，N）模型进行建模，预测下一个序列，同时删除第一个序列，增加最新数据序列作为输入，继续向后进行预测，并且采用平均绝对误差、均方误差、平均百分比误差作为预测结果评判标准，计算过程如式（10）～（12）所示［16］，预测结果对比图如图1、图2所示。

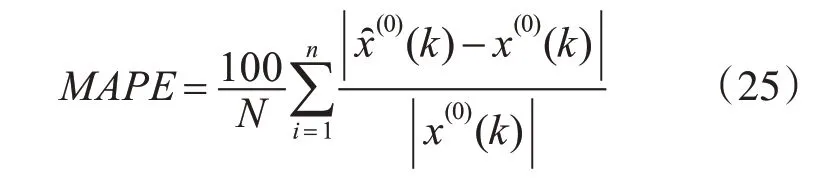
图1 各模型预测结果对比图

图2 各模型预测结果对比图

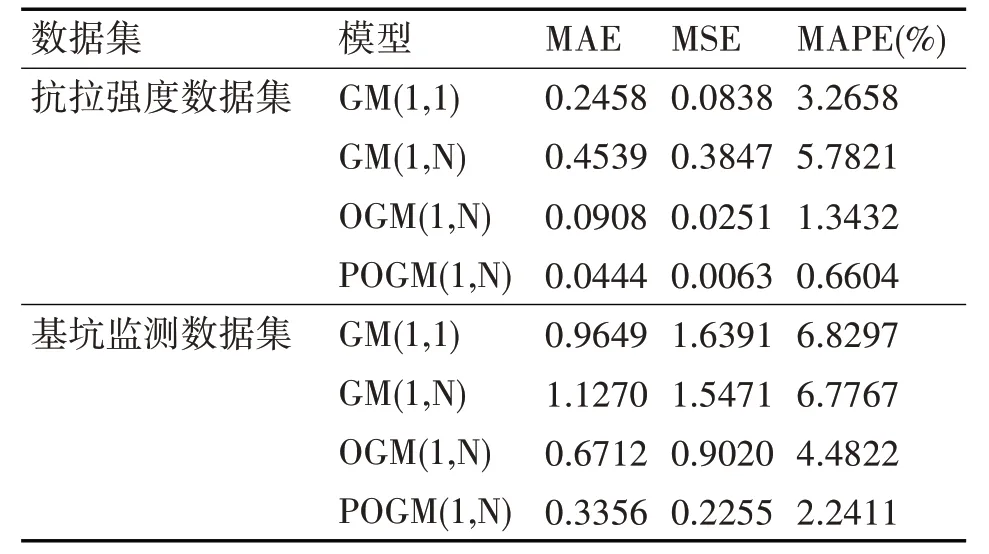
表4 各模型性能对比

从图1 可以发现，在抗拉强度数据集上，GM（1，N）模型预测过程出现较大偏差，GM（1，1）模型除个别点出现较大偏离外，绝大多数点误差相对较小，但GM（1，1）模型没有准确反映出真实数据的变化趋势，POGM（1，N）模型和OGM（1，N）模型充分考虑了数据点之间的变化趋势，预测结果相对稳定。从图2 可以发现，在基坑监测数据集上，传统GM（1，1）模型和GM（1，N）模型的预测结果相对稳定但是误差较大，POGM（1，N）模型和OGM（1，N）模型预测结果更接近于真实值，绝大多数点相对误差较小，预测结果更为稳定。另外，通过表4 中各个模型在表1、表2 数据集上的预测指标对比可以看出，本文所提方法在MAE、MSE 和MAPE 三大指标下的性能相对于GM（1，1）模型、GM（1，N）模型有了较大提升，和OGM（1，N）模型相比，在MAE、MSE 和MAPE 指标上分别下降了0.0464，0.0188，0.6828%和0.3356，0.6765，2.2411%。这说明，本文所提出的POGM（1，N）模型能获得比其他方法更好的预测效果，POGM（1，N）模型预测精度高，更能反映数据的真实变化趋势。

5 结语

本文提出了一种基于粒子群优化算法进行参数寻优求解的GM（1，N）优化模型，该模型采用灰色关联分析法计算提取与参考序列关联度值较高的序列，组成模型的自变量输入序列，并在OGM（1，N）模型的预测原理上优化模型初始条件，根据PSO 算法进行多元变量灰度模型的参数寻优和预测建模，借鉴滑动窗口的思想，依次向后进行序列预测，有效提高了改进模型的适用范围。通过在基坑监测数据集和抗拉强度数据集上的实验，证明了改进模型具有较高的预测精度。