轧机辊缝自动控制系统研究

王 芸

(山西交通职业技术学院,山西太原 030006)

引言

轧机作为钢铁企业重要生产设备，其辊缝控制系统控制性能直接影响轧带品质[1]。只有提高辊缝控制系统控制精度和抗干扰性能，才能获得精度高、符合生产需求的轧带。

樊立萍等[2]将模糊逻辑控制和PID控制结合，构成模糊自适应PID应用于轧机辊缝控制系统，仿真结果表明该控制方法比传统的PID控制有更好的控制效果；崔佳梅等[3]通过PID、神经网络、无模型自适应控制3种算法对轧机辊缝控制系统进行仿真比较，结果表明无模型自适应控制收敛快，稳态误差小，且能提高对扰动和模型变化的鲁棒性；方一鸣等[4]针对轧机辊缝控制系统存在非线性特性、参数不确定性以及控制输入前具有不确定系数的问题，提出了一种自适应反步滑模控制方法，仿真结果表明所设计自适应反步滑模控制器能实现快速准确跟踪，并且对参数变化具有较强鲁棒性；王宪等[5]针对轧机辊缝控制系统内部参数不同和外界干扰不一致造成轧辊压下位置不同步的问题，设计了基于模糊输出反馈的辊缝伺服同步控制系统，仿真结果表明基于模糊输出反馈的控制系统不仅具有较短的同步时间并且跟随误差更小；李建雄等[6]提出一种基于Anti-windup的抗饱和鲁棒动态输出反馈控制算法，将所提出的算法应用于某650 mm轧机辊缝控制系统，其结果验证了所提出算法的有效性；付兴建等[7]针对轧机辊缝控制系统采用了鲁棒H∞控制器对参数摄动等不确定性进行了仿真，结果表明所设计的H∞控制器具有良好的跟踪特性和对参数摄动的鲁棒性；彭珍瑞等[8]在分析数控机床进给伺服系统数学模型的基础上，采用一种基于人工鱼群算法优化PID控制器参数，并与传统的Ziegler-Nichols法进行比较.仿真实验结果表明：人工鱼群PID控制方法的效果明显优于传统的PID控制,具有良好的动态和稳态性能；徐秀芬[9]针对电液比例系统PID控制参数整定问题，提出了基于蚁群算法的PID参数优化方案，并给出了具体的实现步骤，结果表明：VACA-PID控制器具有良好的静、动态性能，完全能达到电液比例控制系统的要求。

以上研究成果可以看出，目前针对轧机辊缝控制系统的研究较多，但主要集中于系统阶跃响应性能的研究，研究工况单一，控制器无法满足轧机复杂工况对系统控制性能的要求。因此，本研究介绍了轧机辊缝控制系统，建立了系统开环传递函数，采用人工鱼群算法和蚁群算法对PID控制器进行参数优化，基于Simulink比较了优化后的系统响应性能和抗干扰性能。

1 轧机辊缝控制系统原理及数学模型建立

控制轧机工作辊运动的执行机构为2个液压缸，如图1所示，可以控制工作辊在垂直方向运动。液压缸位移由测厚仪反馈给计算机，其运动由伺服阀阀芯运动进行控制，从而实现对轧机辊缝的精确控制。轧机辊缝控制系统如图2所示。

分析图2可以得出，轧机辊缝控制系统为液压缸位置控制，其数学模型建立过程目前比较完善，因此本研究将系统关键部分数学模型列出[10]。

伺服放大器数学模型为：

I=K1Δu

(1)

式中,Δu—— 输入电压，V

I—— 输出电流，A

K1—— 放大系数，A/V

伺服阀数学模型为：

(2)

式中，xv—— 阀芯位移，m

Kb—— 阀芯位移与电流增益系数，m/A

图1 轧机辊缝液压原理图

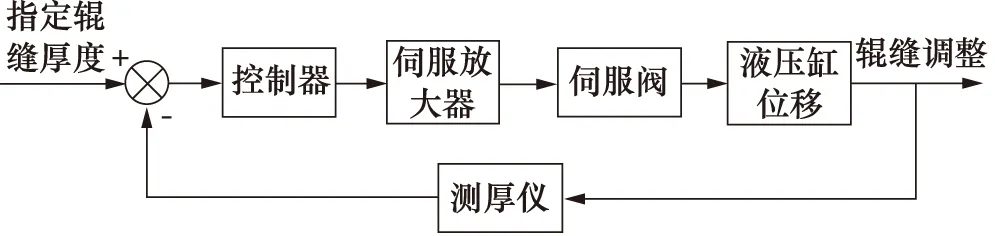
图2 轧机辊缝控制系统

测厚仪数学模型为：

Uf=Kfxp

(3)

式中，Kf—— 厚度反馈增益，V/m

Uf—— 反馈电压，V

xp—— 活塞输出位移，m

活塞位移xp对阀芯位移xv的传递函数为：

(4)

式中,Kq为伺服阀流量增益，m2/s。

活塞位移xp对负载干扰FL的传递函数为：

(5)

式中,Vt为液压弹簧刚度最小时的总工作容积，m3。

下面确定系统中主要参数。液压缸选用原有液压缸，半径为39.4 mm。流量系数取值范围0.6～0.62，本研究取0.62。放大器放大系数及伺服阀固有频率、节流口面积梯度、油液密度、厚度反馈增益等可查阅相关获得，系统主要参数见表1。

表1 系统主要参数

将各参数代入式(4)和式(5)，活塞位移xp对阀芯位移xv的传递函数为：

(6)

活塞位移xp对负载干扰FL的传递函数为：

(7)

2 轧机辊缝控制系统控制器设计

轧机辊缝控制系统为典型的液压缸位置控制，工业上常采用PID控制器，常规PID控制器如下式所示：

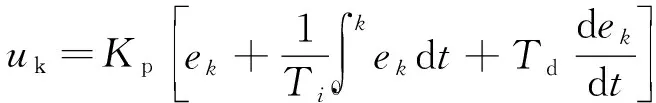
(8)

本研究选用更适用于计算机控制的位置式PID控制器[11]。假设采样周期为T，采样时间为t，则离散PID可表示为：

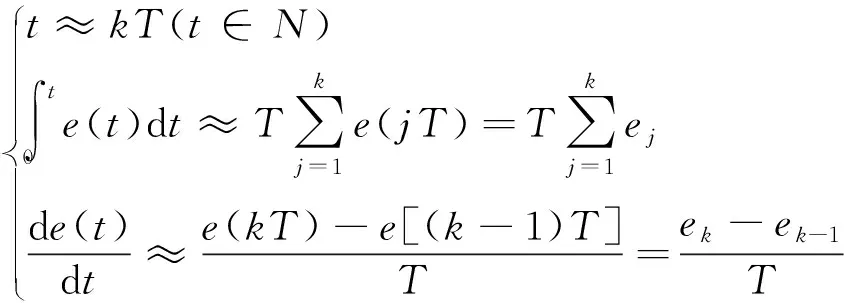
(9)

将式(9)代入式(8)中即可提到位置式PID控制器的表达式，表达式如式(10)。

式(10)中,β为积分项开关系数，β取值遵循下式：当ek≤ε时，β=1；当ek>ε时，β=0。其中ε为阈值。ε取值将直接影响系统性能，根据轧机实际工况，这里选取ε为0.01。

PID控制器中最重要的是其3个参数的优化。下面分别采用蚁群算法和人工鱼群算法对PID控制器的3个参数进行优化。

首先采用蚁群算法优化PID 3个参数[12]。蚁群算法可模仿真实的蚂蚁行为，蚂蚁之间通过一种外激素物质进行信息传递，蚂蚁在运动路径上留下这种信息素，蚁群集体行为表现出一种信息正反馈现象。蚁群算法优化PID结构框图如图3所示，其优化具体流程如图4所示。

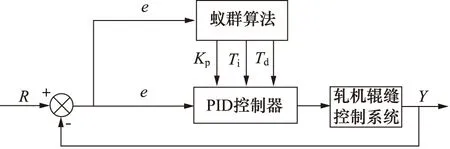
图3 蚁群算法优化PID参数结构框图

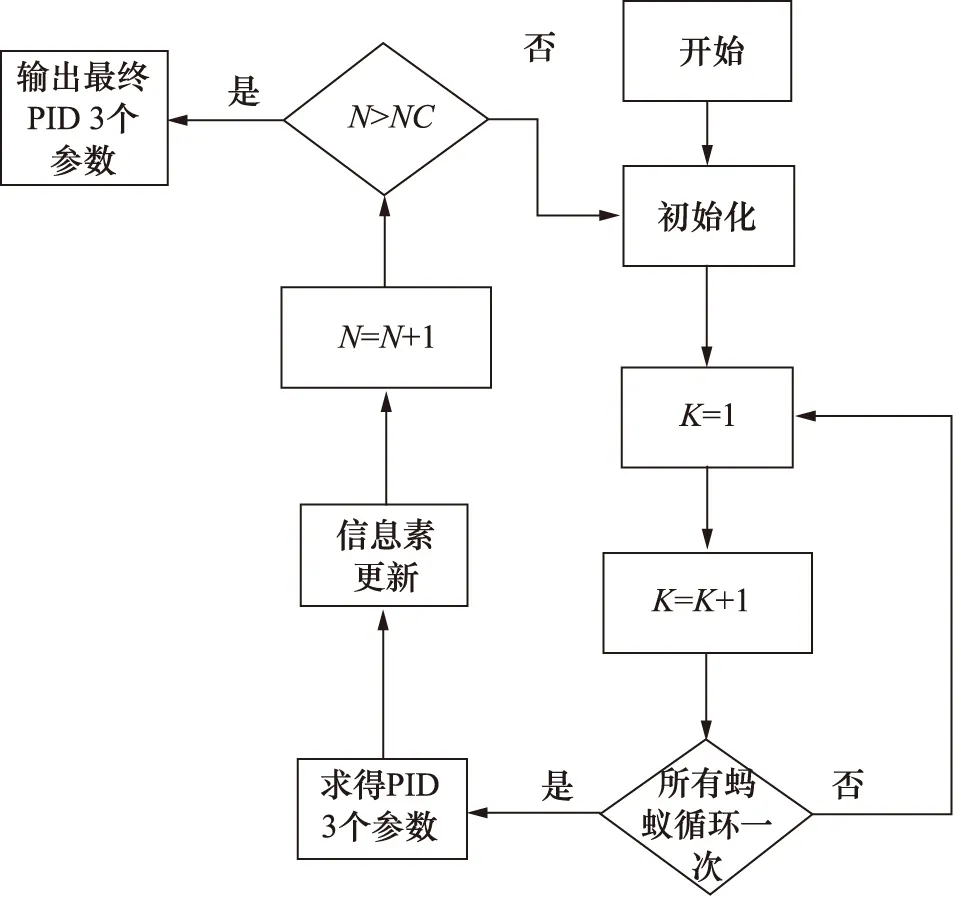
图4 蚁群算法优化PID参数流程图

图4中信息素更新变化按式(11)所示：

τ(xn,ynm,t)=ρτ(xn,y,t)+Δτ(xn,ynm,t)

(11)

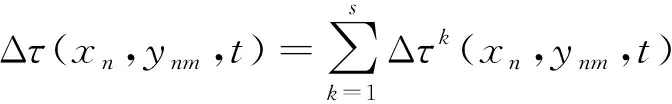
(12)

Δτk(xn,ynm,t)=Q/Fk

(13)

式中，ρ为挥发因子，0<ρ<1；Fk为第k只蚂蚁的目标函数值；Q为蚂蚁完成一次探索释放信息素总量，为一个常数。

根据蚁群算法优化PID参数流程在MATLAB软件中进行编程。部分编程程序如图5所示。

图5 蚁群算法优化PID参数程序

具体过程为：设置蚂蚁数量为40，挥发系数ρ取0.8，信息启发因子α取0.4，最大迭代次数NC取100。限定截割头位姿调节器3个参数Kp，Ti和Td范围设置为(0，30)。采用ITAE作为目标函数，如式(14)所示:

(14)

经过100代迭代，可获得蚂蚁算法优化后的3个参数，如表2所示。

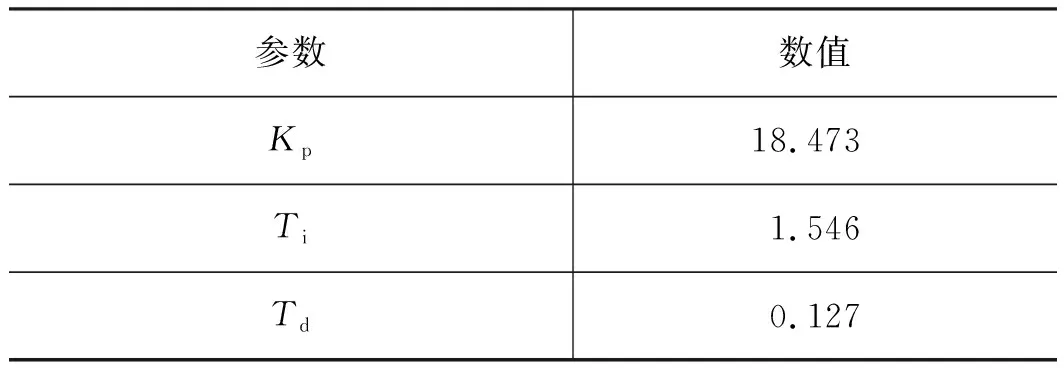
表2 蚂蚁算法优化参数结果

再次采用人工鱼群算法优化PID 3个参数[13]。人工鱼群算法通过模仿鱼群易在富集营养较多的地方进行聚集的特点对鱼群的觅食行为进行最优求解。人工鱼群算法具有全局快速收敛的优点，相比蚁群算法具有更强的跳出局部最优的能力。如图6所示为其结构框图。人工鱼群算法优化PID 3个参数流程，如图7所示。

图6 人工鱼群算法优化PID控制器

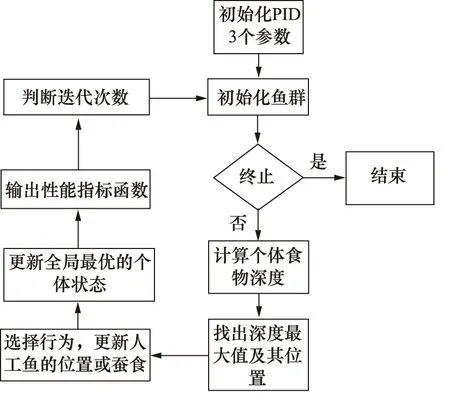
图7 人工鱼群算法优化PID参数流程图

根据人工鱼群算法优化PID参数流程在MATLAB软件中进行编程。部分编程程序如图8所示。

图8 人工鱼群算法优化PID控制器程序

具体过程如下：设置人工鱼的初始种群大小为50，步长为0.8，视野visual=40，尝试次数try-umber=40，拥挤度因子σ=10，最大迭代次数为200，搜索范围设置为(0，30)。采用ITAE的倒数作为目标函数[14]，如式(15)所示:

(15)

经过200代迭代，鱼群适应度提高，可获得人工鱼群算法优化后的3个参数，如表3所示。

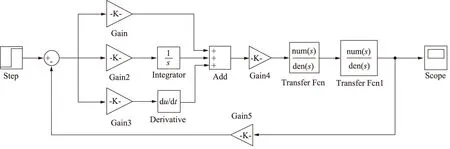
图9 截割头位姿控制系统仿真模型

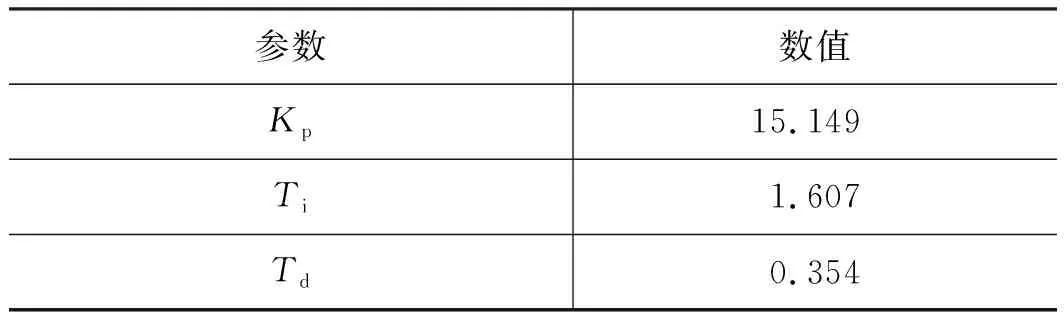
表3 人工鱼群算法优化参数结果

3 轧机辊缝控制系统仿真

由上述所建立的轧机辊缝控制系统传递函数，在Simulink中建立系统仿真模型，如图9所示。本研究对系统施加阶跃信号以及不同频率随机信号，比较经2种算法优化的系统响应性能和抗干扰性能。

首先对模型加入经2种算法优化的PID 3个参数，对系统施加阶跃信号，仿真得到基于2种算法优化的系统阶跃响应曲线，如图10所示。

图10 阶跃响应曲线对比

本研究采用超调量、调整时间和稳态误差3个指标对阶跃信号响应曲线进行评价，评价结果对比如表4所示。

从表4可得，人工鱼群算法相比于蚁群算法，阶跃响应曲线超调量下降了13.725%，调整时间缩短了20.287%，稳态误差降低了29.167%，因此经人工鱼群算法优化的系统响应性能优于蚁群算法。

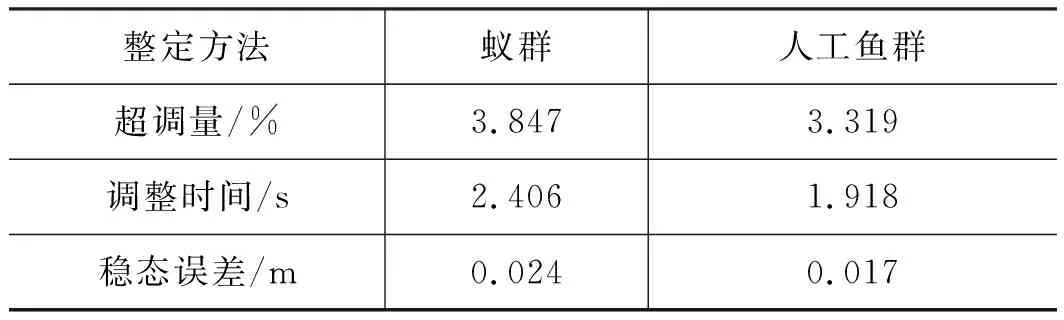
表4 阶跃响应结果对比

下面对系统施加阶跃信号的同时，施加干扰力信号，比较2种算法优化的系统抗干扰性能。

仿真得到基于2种算法优化的系统在干扰力作用下的阶跃响应曲线，如图11所示。

图11 阶跃响应曲线对比(施加干扰力)

表5为用2种算法优化的系统在干扰力作用下响应曲线超调量、调整时间和稳态误差的结果对比。

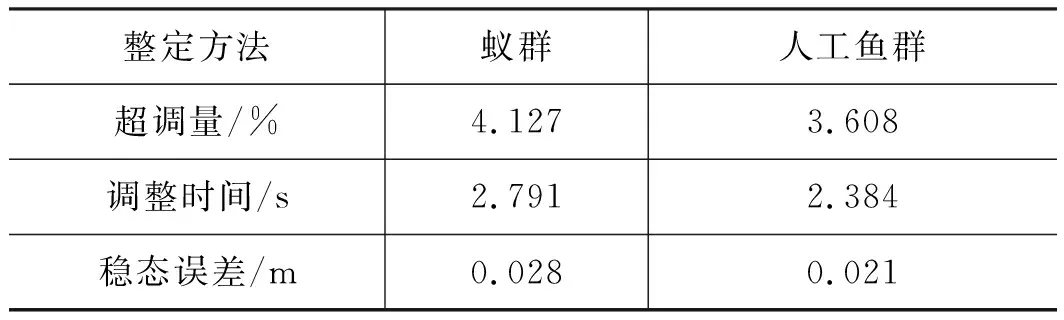
表5 干扰力作用下仿真结果对比

对比数据发现：在干扰力作用下，采用人工鱼群算法优化的系统，响应曲线超调量下降了12.576%，调整时间缩短了14.583%，稳态误差降低了25%，因此人工鱼群算法优化的系统抗干扰性能优于蚁群算法。

最后采用Random Number模块对系统施加1,2,4,8 Hz随机信号。仿真得到系统随机信号响应曲线如图12～图15所示。

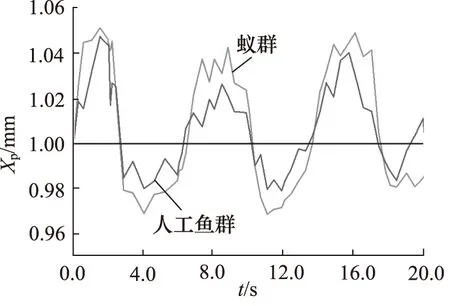
图12 1 Hz随机信号系统响应曲线对比

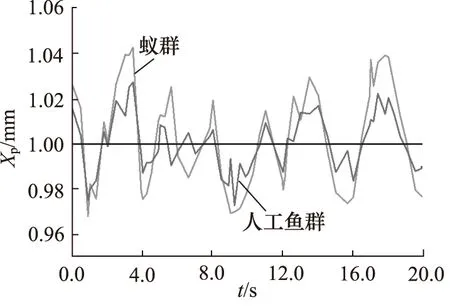
图13 2 Hz随机信号系统响应曲线对比

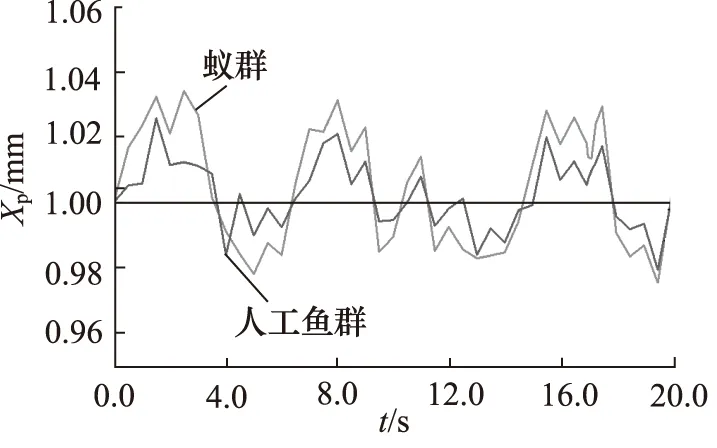
图14 4 Hz随机信号系统响应曲线对比

图15 8 Hz随机信号系统响应曲线对比

不同频率随机信号下的系统响应波动范围对比如表6所示。

表6 不同频率随机信号的响应波动范围对比

从表6可以看出：随机信号频率增加，2种算法下的系统响应曲线波动范围均逐渐减小；不同频率下，相比蚁群算法，采用人工鱼群算法的随机信号响应曲线波动范围较小，因此采用人工鱼群算法优化的系统对随机信号的响应性能优于蚁群算法。

4 结论

为提高轧机辊缝控制精度，建立了轧机辊缝控制系统开环传递函数，分别采用蚁群算法和人工鱼群算法对PID 3个参数进行优化，并对优化后的系统控制性能进行了仿真分析。主要得出以下结论：

针对轧机辊缝控制系统，人工鱼群算法相比蚁群算法，在加入干扰力和不加干扰力两种情况下，系统阶跃信号响应超调量下降了12%以上，调整时间缩短了14%以上，稳态误差降低了25%以上；对于不同频率随机信号来说，采用人工鱼群算法的系统随机信号响应曲线波动范围均小于采用蚁群算法的系统随机信号响应曲线波动范围。因此经人工鱼群算法优化的轧机辊缝控制系统对阶跃信号和随机信号的响应性能以及对干扰力的抗干扰性能均优于蚁群算法优化的系统。