液压调速系统遗传算法优化前馈-反馈PID控制
2020-12-04魏晓朝倪向东韩双蔓钟春发
魏晓朝,倪向东,赵 新,李 申,韩双蔓,钟春发
(石河子大学机械电气工程学院,新疆石河子 832000)
引言
电液比例控制技术因其突出的优点,如高精度控制被控对象、环保节能以及并不复杂的工作过程,而被广泛应用于军事、金属冶炼、船舶、铁路交通等众多工业领域[1-2]。其中,液压调速系统是一个重要的应用方向。国内外诸如拖拉机和采棉机等某些输出功率较大的非道路车辆,大多配有液压机械无级变速器(HMCVT),不仅驾驶员可以高度关注车辆行驶过程,缓解驾驶疲劳,而且车辆作业效率也得以提高。但影响HMCVT传动效率的因素众多,主要为液压系统,所以液压调速系统的性能在一定程度上影响着HMCVT的调速性能[3-5],研究液压调速系统的动态响应对提升HMCVT的调速特性有重要意义。
为了能够提升液压调速系统的速度调节性能,有必要引入合适有效的控制策略。范宇恒等[6]利用STM32单片机设计出在转速扰动的情况下,输出端仍然可以稳定输出转速的泵控马达调速系统。李万国等[7]在分析完由“变量泵+变量马达”组成的容积调速回路后,提出了一种基于给定值静态并结合前馈补偿-反馈控制的转速控制方法,提升了系统的阶跃响应性能。曹付义等[8]为了解决液压机械无级变速器传动系统在阶跃扰动下输出速度波动剧烈的问题,提出了一种基于双子系统前馈补偿模糊PID控制的速度波动抑制方法,成功抑制了系统转速的波动程度。成钊等[9]为了解决泵控马达系统输出速度无规律波动的问题,提出了一种基于系统输出速度偏差及其变化率的非线性PID控制算法,有效提升了系统速度波动抑制性能。赵新等[10]为了解决采棉机行驶系统中机液复合传动系统控制精度低等问题,提出了一种基于液压行驶系统的前馈补偿模糊自适应PID控制算法,提高了控制精度。但目前大多数学者偏向于利用控制算法对液压调速系统输出转速进行控制[11],对液压调速系统参数优化与控制算法相结合的研究较少。
本研究主要针对液压机械无级变速器中液压调速系统输出转速波动的问题,提出了一种基于该系统的遗传算法优化前馈-反馈+PID转速复合控制方法,旨在提高系统的动态响应性能和转速控制精度,以期为工程上的实际应用奠定基础。
1 系统组成与控制系统结构
1.1 系统组成
图1为液压调速系统结构图,核心为容积调速回路,由变量泵和定量液压马达组合而成。液压调速系统通过调节变量泵排量比来控制液压马达转速。首先由指令元件向系统输入信号并通过比例放大器放大,用于调节电液比例阀的流量,然后液压缸活塞位移量也会发生改变,从而调整变量泵斜盘倾角以改变变量泵排量比,最终控制液压马达转速。
1.2 数学模型建立
1) 电液比例方向控制阀阀芯位移函数
(1)
式中,xsv—— 电液比例方向控制阀阀芯位移
If—— 比例放大器输出电流信号
Ksv—— 控制阀增益系数
ξsv—— 控制阀液压阻尼比
ωsv—— 控制阀及衔铁固有频率
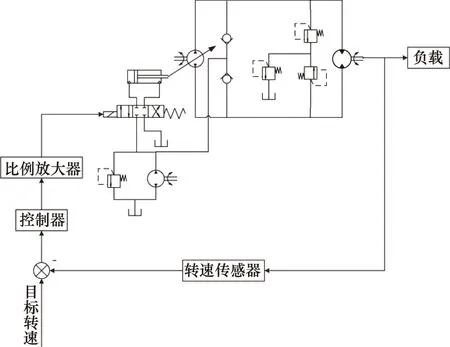
图1 液压调速系统结构图
2) 液压缸活塞位移函数
(2)
式中,xhp—— 液压缸活塞位移
Kfg—— 控制阀流量放大系数
ωhp—— 液压缸活塞固有频率
ξhp—— 液压缸阻尼比
A—— 液压缸活塞作用面积
3) 变量泵斜盘倾角函数
(3)
式中,r—— 变量泵斜盘倾角
Rp—— 变量泵斜盘旋转半径
4) 定量马达轴角速度函数
(4)
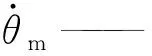
Kp—— 变量泵排量梯度
Np—— 变量泵转速
Dm—— 定量马达排量
ωm—— 液压固有频率
ξm—— 阻尼比
5) 外负载转矩函数
(5)
式中,Tf—— 外负载转矩
Cl—— 系统总泄漏系数
Vc—— 系统工作腔室总容积
β0—— 液压油弹性模量
1.3 控制系统结构
针对搭载液压机械无级变速器的非道路车辆多在重载荷、路况复杂多变的情况下工作,容易引起液压泵控马达调速系统中液压马达输出转速剧烈地波动,导致系统稳定性降低以及动态性能下降等问题,提出一种基于液压调速系统的遗传算法优化前馈-反馈+PID转速复合控制方法,控制系统结构如图2所示。
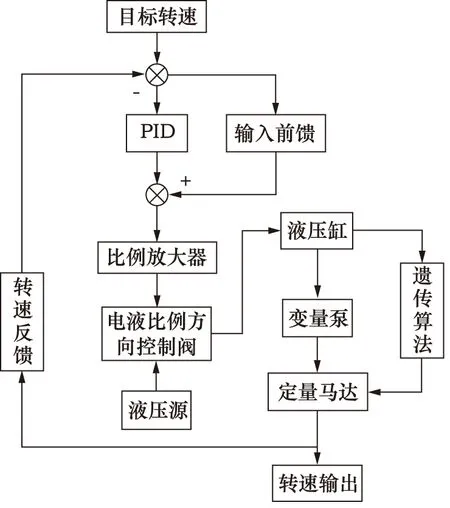
图2 控制系统结构
液压调速系统转速控制系统包括3部分:转速闭环反馈控制系统、前馈补偿控制系统和遗传算法优化控制系统。转速闭环反馈控制系统采用传统PID控制,对系统转速进行基本地调节;考虑到传统液压调速回路存在动态响应速度慢及溢流能量损失等问题,引入前馈补偿控制部分。该部分控制原则是,根据液压调速系统的期望转速,求解出相应补偿基准值,使得整个调速系统响应速度提高,节能性增强,对马达输出转速控制更加精确,最终系统稳态误差减小,调速系统输出转速稳定;遗传算法优化控制部分对液压马达参数进行优化,使得液压系统性能提高。
2 基于遗传算法参数优化
2.1 遗传算法原理
遗传算法产生于达尔文提出的进化论和自然选择学说,可以模拟生物进化论和自然界遗传机制,具有自适应性和全局性的概率搜索能力,最大优势为可以避免所需优化参数在优化期间因为落入局部最优点而以之为最优值的问题[12]。遗传算法最优解求解过程[13]如图3所示。
2.2 优化目标
本研究参数优化针对泵控马达系统进行。由式(4)、式(5)可知,影响系统性能的参数有:液压固有频率、阻尼比、液压马达排量、负载转动惯量及液压油弹性模量。通过理论分析可得液压马达排量与负载转动惯量对系统输出转速影响程度较大。图4和图5分别为系统输出转速随液压马达排量与负载转动惯量变化的曲线,当液压马达排量增加时,泵控马达系统的响应时间会减少,但当排量值过大时,泵控马达系统响应时间减少地不仅不明显,反而系统输出转速的波动程度会增加,则相应地导致系统稳定性下降;当负载转动惯量不断增加时,泵控马达系统的响应时间增加地较为明显,但若负载转动惯量取值较小时,系统响应时间虽会大幅减少,同时也会使马达输出转速波动程度增加。因此优化目标设置为系统输出转速到达目标转速所需的最少时间,优化参数设置为液压马达排量和负载转动惯量。
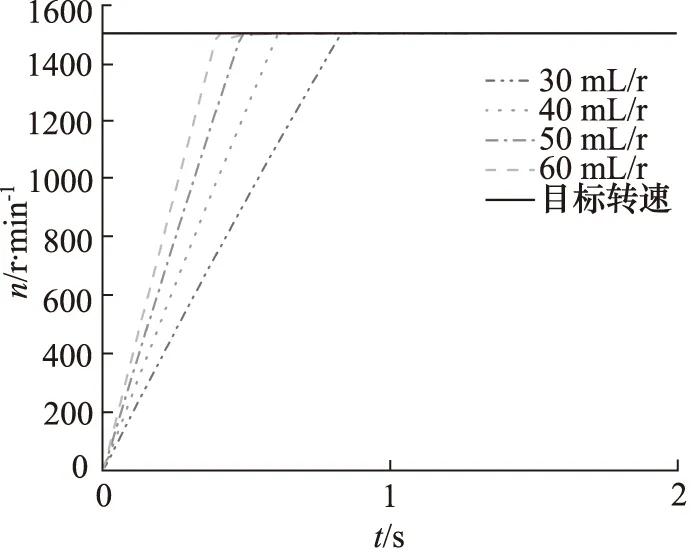
图4 系统输出转速随马达排量变化曲线

图5 系统输出转速随负载转动惯量变化曲线
2.3 系统优化分析
设置种群规模为60,遗传概率为80%,最大迭代次数为50,变异概率为10%。设置优化参数范围:定量马达排量为0~70 mL/r ,负载转动惯量为0~1 kg·m2。得出最优马达排量为61 mL/r,最优负载转动惯量为0.115 kg·m2。在最优参数下,泵控马达系统响应特性曲线如图6所示,马达转速响应超调量为0.16%,到达目标转速的时间为0.8 s,较未优化参数下时间缩短3.3 s,结果较为理想。
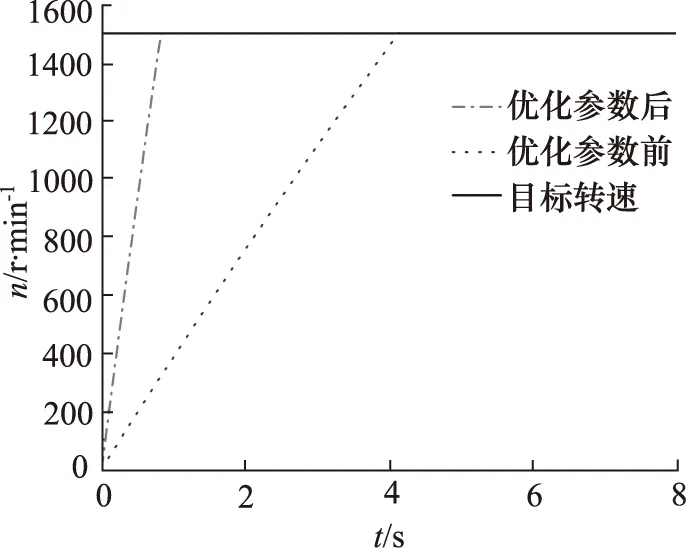
图6 优化前、后泵控马达系统响应特性曲线
3 基于液压调速系统的遗传算法优化前馈-反馈+PID控制仿真结果与分析
根据图2给出的控制系统结构图在AMESim软件和MATLAB/Simulink软件下建立液压调速系统的仿真模型,主要包括PID控制器、前馈补偿器、转速转矩传感器、电液比例阀、液压缸、变量泵和定量马达,关键参数如表1所示。
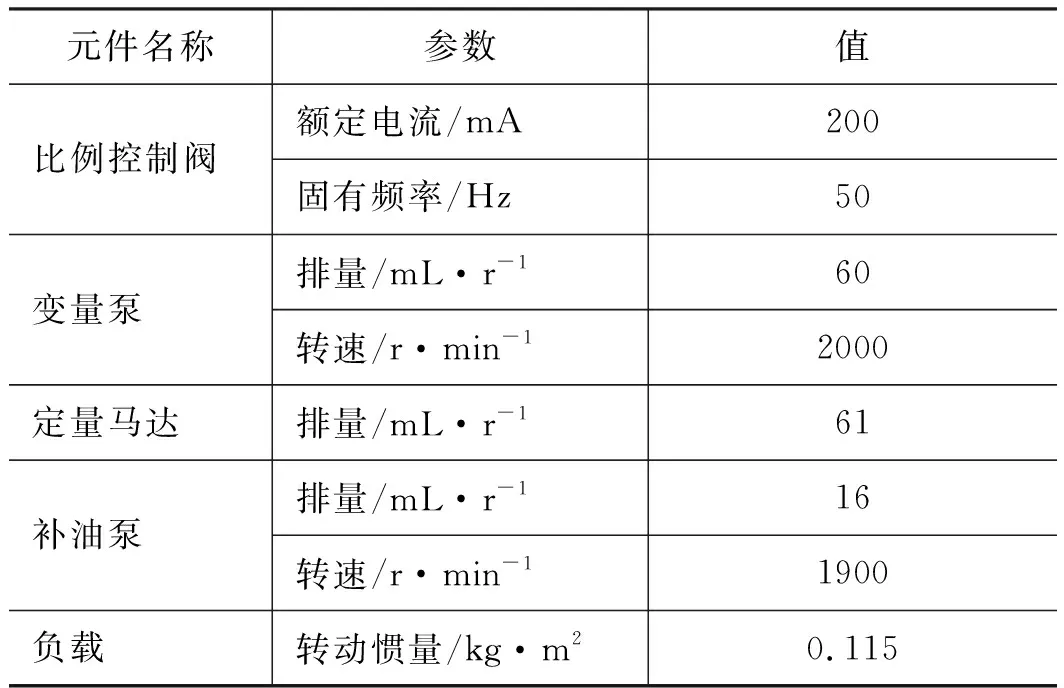
表1 液压调速系统参数
特定的非道路车辆在起步时液压调速系统的输出转速为1000 r/min。分别采用传统PID转速控制方法以及遗传算法优化前、后的前馈-反馈+PID转速复合控制方法对系统输出转速进行控制,对比结果如图7所示。
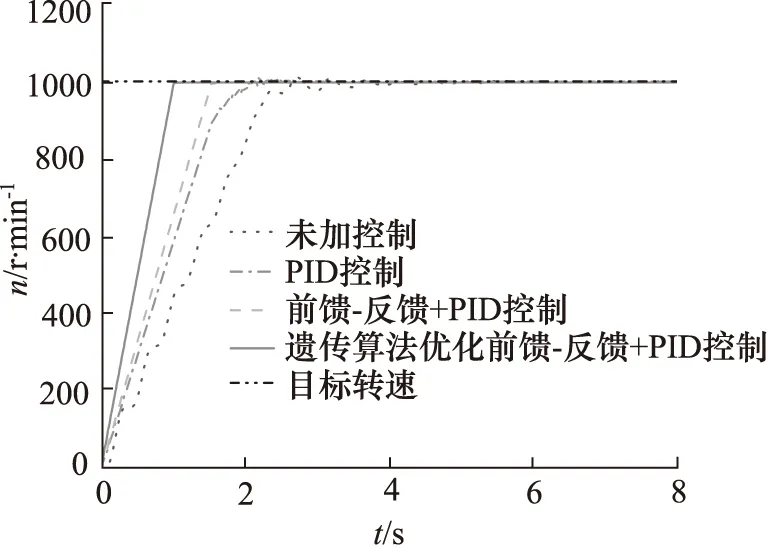
图7 液压调速系统输出转速仿真曲线
当系统采用传统PID控制方法时,系统输出转速的超调量为0.56%,稳定调节时间为3.6 s,仿真曲线基本稳定在马达期望输出转速1000 r/min附近。当系统采用前馈-反馈+PID控制方法时,系统输出转速超调量为0.43%,稳定调节时间为1.7 s,相较于传统PID控制,超调量减少23.2%,稳定调节时间缩短1.9 s,仿真曲线也基本稳定在马达期望输出转速1000 r/min 附近,系统响应速度也有所提高。当系统采用遗传算法优化前馈-反馈+PID控制方法时,系统输出转速的超调量为0.35%,稳定调节时间为1.2 s,相较于传统PID控制和前馈-反馈+PID控制,超调量分别减少37.5%和18.6%,稳定调节时间分别减少2.4 s和0.7 s,仿真曲线仍能稳定在马达期望输出转速1000 r/min附近,且系统输出转速波动抑制效果明显。
针对负载转矩会对液压调速系统产生冲击影响,在第5 s时对该系统突加100 kg·m2的负载转矩。分别采用前馈-反馈+PID转速控制方法及遗传算法优化前馈-反馈+PID转速复合控制方法对突加负载后的系统科学控制,响应结果如图8所示。
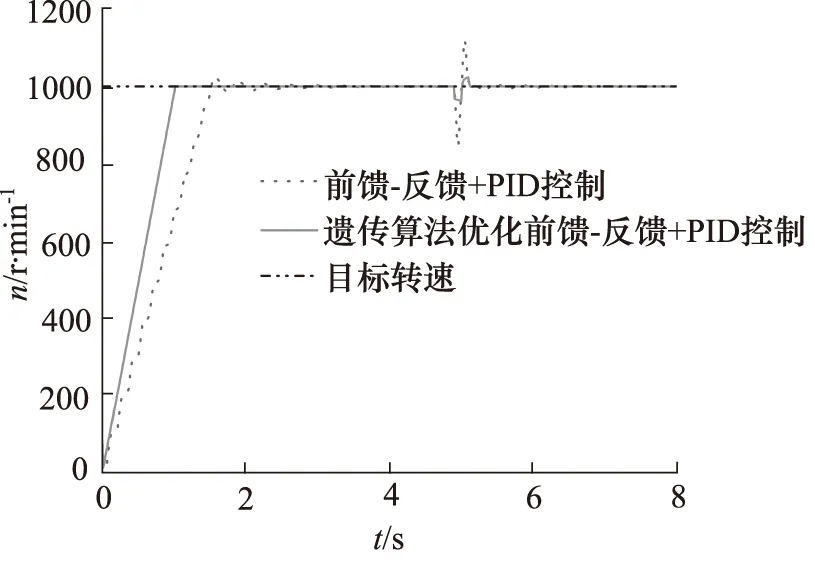
图8 施加负载后液压调速系统输出转速仿真曲线
当施加100 kg·m2的负载转矩后,经过遗传算法优化前馈-反馈+PID控制后的系统调整时间缩短、响应速度提高,转速超调量明显减少。
综上所述,所提出的遗传算法优化前馈-反馈+PID转速复合控制方法具有良好的控制性能,能大幅提高系统的调速性能及稳定性,验证了该控制方法具有准确性及可行性。
4 结论
通过分析液压机械无级变速器中液压调速系统的工作原理及数学模型,研究液压调速系统对输出转速稳定性的控制,主要得出如下结论:
(1) 针对液压动力路中受负载干扰的液压马达转速稳定输出问题,提出一种基于液压调速系统的遗传算法优化前馈-反馈+PID转速复合控制方法;
(2) 利用AMESim软件和Simulink软件建立了液压调速系统的物理模型,并对系统的动态响应特性进行仿真;
(3) 仿真结果表明,所提出的控制方法具有良好的控制效果。基于遗传算法优化的液压调速系统在前馈-反馈+PID控制下的输出转速超调量及稳定调节时间明显减少、抗负载干扰能力增强、能迅速对输入信号进行跟踪。
