湿滑路面汽车轮胎滑水性能影响因素仿真

2020-12-04张丽霞郑超艺杨朝会潘福全

科学技术与工程 2020年30期

张丽霞，郑超艺，杨朝会，郭峰，潘福全，张辉

(1.青岛理工大学机械与汽车工程学院，青岛 266520;2.青特集团有限公司技术中心，青岛 266109)

如今拥有优良的湿滑性能和噪声振动性能已经成为轮胎公司在轮胎研发时考虑的重要因素和基本要求。Pan等[1]明确提出因为雨天路面湿滑，轮胎与路面的附着能力变差，雨天时的汽车交通事故率明显高于晴天时的事故率，可能会超过2～3倍。因此，探究轮胎的湿滑性能具有重要的意义[2]。Okano等[3]基于MSC.Dytran数值仿真软件，分析了轮胎结构的大变形和其引起的水流流动情况，得到了4种不同花纹结构轮胎的临界滑水速度。Ong等[4]根据固体力学和流体动力学，研究了轮胎在湿滑路面上行驶时轮胎、水膜、路面三者之间的耦合关系，发现随着轮胎结构的改变，地面法向力、地面纵向力、轮胎与路面的接触面积和动水压力都会发生变化。Ong等[5]对以上模型进行了改进，基于Adina软件，仿真研究了轮胎的滑水现象，得到了轮胎滑水速度。研究发现水膜厚度、汽车行驶速度、轮胎充气压力和轮胎负荷都会影响轮胎的湿滑性能。吴琦等[6]基于有限元软件FLUENT，研究了轮胎与水膜的相互作用，仿真出在不同的轮胎速度、胎面花纹和水膜厚度时，轮胎受到的水流作用力。杨军等[7]研究发现了路面湿滑时轮胎与路面间附着系数的变化规律。周海超等[8-10]基于计算流体动力学的方法，提出了改变沟槽形状和排列形式可以直接影响轮胎的滑水性能，并采用计算流体动力学，引入仿生减阻理念，提出沟槽底部减阻结构(仿生非光滑花纹沟)的存在可以延缓轮胎滑水现象的产生，提升轮胎的抗滑水性能。

前人研究主要以动水压强或附着系数为指标研究轮胎滑水性能，基于轮胎花纹沟槽深度对滑水性能的影响研究较少，仅文献[8-10]基于计算流体动力学方法，研究了纵向花纹沟深度对滑水性能影响，通过改变沟槽底部减阻结构来提高轮胎滑水性能。临界滑水速度对驾驶员的安全行车有一定的指导意义，因此以临界滑水速度为指标，基于ABAQUS仿真软件，在考虑轮胎花纹沟槽深度等多种因素对汽车滑水性能的影响方面具有一定的创新性。

基于ABAQUS建立了轮胎有限元模型，然后将轮胎与路面水膜进行耦合建模。基于流固耦合仿真分析汽车在湿滑路面上行驶时的滑水性能，以临界滑水速度为指标，研究不同水膜厚度、充气压力、轮胎负载和花纹沟槽深度等因素对轮胎滑水性能的影响。

1 轮胎滑水理论

1.1 轮胎变形体的运动描述及边界方程

在模型建立中，轮胎变形应用Lagrangian方法分析，水流变形应用欧拉方法分析。在不考虑轮胎阻尼系数的假设下，建立的轮胎运动方程为

(1)

式(1)中：M为轮胎的质量矩阵；U为轮胎的节点位移；Fint为轮胎内部载荷；Fext为轮胎外部载荷。

轮胎的初始和边界条件如下。

(1)初始条件：

(2)

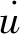
(2)边界条件：

(3)

主要对轮胎进行两个仿真计算过程：轮胎充气和加载隐式计算过程、轮胎滑水仿真显式计算过程，隐式运算用Newmark法，显式运算用中心差分法。

1.2 水流控制方程

分别建立水流的质量守恒，动量守恒和能量守恒方程。

(1)质量守恒方程：

(4)

式(4)中：ρw为水流密度；v为流体运动速度。

(2)动量守恒方程：

(5)

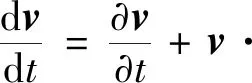
(6)

式(5)中：bw为水流承受的重力；σw为流量柯西应力。

(3)能量守恒方程：

(7)

1.3 水流的初始条件和边界条件

(1)初始条件：

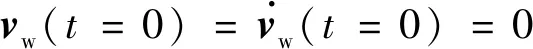
(8)

(2)边界条件：在轮胎和水流的接触边界，水流不应该渗入到轮胎中，所以边界条件为

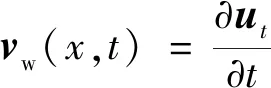
(9)

式(9)中：ut为轮胎在水流作用下的位移。

在轮胎与水流没有接触的区域，需满足：

nσw=FT

(10)

式(10)中：n为水流与轮胎接触方向向外的方向向量；FT为水流的外部作用力。

因为水流运动的大变形不能用Lagrangian网格进行计算，所以用Euler网格描述水流的运动。水流的质量守恒和动量守恒方程在欧拉坐标形式下，可表示为

(11)

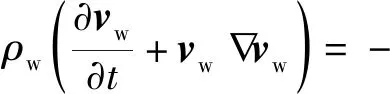
(12)

式(12)中：p为流体静压强；η为水流黏性系数。

1.4 水流自由表面构建

如果水流网格渗入到轮胎网格内部，将使整个流固耦合模型仿真计算错误。水流自由表面采用流体体积方法(volume of fluid，VOF)来构建。流体体积法对网格的变形无任何约束，因此可以应用到水流的自由流动和大变形中，应用于轮胎导致的水流的流动细节处理中非常合适。令F(x,t)表示在t时刻，x节点位置水流体积与网格体积之比，则可与连续方程类似的推导出体积守恒方程：

(13)

2 轮胎有限元模型建立

2.1 轮胎二维有限元模型建立

研究的轮胎规格为205/55R16，由于轮胎断面的对称性，按照轮胎型号尺寸要求，画出轮胎二维半截面几何模型。然后建立材料模型数据库，并对轮胎截面模型进行网格处理。

2.2 轮胎三维有限元模型建立

在inp文件中获取二维的轮胎网格节点信息，然后通过输入命令关键词的方式，将完成轮辋装载和充气的轮胎绕轴线旋转360°生成轮胎三维模型[11]。图1为建立的光面轮胎三维模型，采用相同的方法生成带有纵向花纹的轮胎三维模型。

图1 轮胎三维有限元模型Fig.1 3D finite element model of tire

2.3 流固耦合建模

利用ABAQUS平台建立了轮胎滑水耦合模型。分别建立空气层模型、水膜层模型和刚体路面模型，然后与轮胎模型进行耦合建立轮胎滑水流固耦合模型，如图2所示。

图2 轮胎滑水模型Fig.2 Model of tire hydroplaning

3 模型验证及轮胎滑水过程分析

3.1 仿真与试验结果对比分析

径向刚度表征轮胎的稳态力学性能。试验测量方法是采用平板试验台对轮胎施加垂直方向载荷，软件仿真方法首先模拟轮辋的固定过程，然后模拟轮胎充气过程，最后在轮胎中心处建立Point，对轮心继续施加载荷[12]。为了验证所建轮胎模型的可靠性，将试验所得数据与ABAQUS仿真数据对比。刚度拟合及误差分析结果如表1所示。

由误差结果(表1)可以看出，试验所得的径向刚度数据与建立的轮胎模型仿真数据相差不大，相对误差在2%以内，可以验证：①利用ABAQUS建立的有限元轮胎模型径向刚度特性是有效的。②在建立模型时，对轮胎结构的简化处理、各种轮胎材料的选择等前处理过程是合理的。③轮胎模型有效。

表1 轮胎径向刚度误差分析Table 1 Radial stiffness error analysis of tires

3.2 轮胎滑水模型的可靠性验证

目前美国航空航天局试验得出的NASA公式是界内公认的[13]，经验公式为

(14)

式(14)中：P为充气压力;vc为轮胎的临界滑水速度。

对轮胎模型进行仿真计算和经验公式计算，轮胎负载设置为4 000 N，轮胎气压设置为220 kPa和240 kPa，计算结果如表2所示。

表2 临界滑水速度对比Table 2 Comparison of critical hydroplaning speed

由经验公式和仿真的临界速度对比分析可得，增加轮胎气压，美国国家航空航天局(National Aeronautics and Space Administration，NASA)经验公式和仿真计算所得的临界滑水速度都会变大，两者的变化趋势是一致，说明滑水模型是可靠的；由于纵向花纹轮胎的湿滑性能不如越野花纹轮胎，所以仿真的临界滑水速度小于经验公式计算得到的临界滑水速度。

3.3 轮胎滑水过程分析

图3所示为轮胎在湿滑路面上行驶时与水膜的接触情况，当轮胎与水膜刚刚接触时，轮胎尚未挤压水膜，轮胎充分与地面接触，可以充分发挥轮胎与地面的最大附着利用率；当车辆继续行驶，轮胎开始挤压水膜，轮胎和水膜都发生变形，此时在轮胎与地面接触区有部分水流存在，水膜起到润滑的作用，导致轮胎的地面附着系数利用率下降；如果车速继续增大，轮胎与路面间的水流不能及时排出，由于水流的运动产生动水压强作用于轮胎表面，直至动水压力等于轮胎载荷，此时轮胎完全脱离地面，浮于水膜之上，轮胎的地面附着系数利用率为0，轮胎发生完全滑水现象[14]。

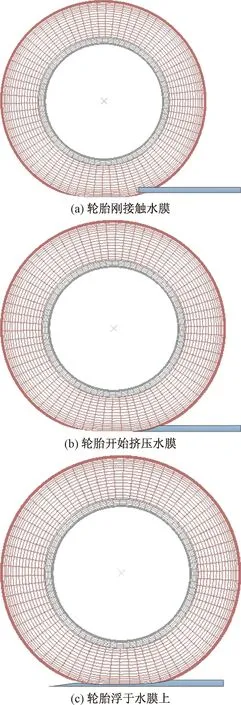
图3 轮胎与水膜接触变化情况Fig.3 The change of the tire contact with the water film

在ABAQUS的inp文件中，定义流体体积分数作为场输出变量[15]。如图4所示，当轮胎滚动经过10 mm水膜时，不同时刻水流的运动情况。

图4 不同时刻水流运动状态Fig.4 The state of flow motion at different times

4 轮胎模型的静态分析

在设置轮胎与路面接触对时，将路面设置为主面，轮胎设置为从面。继续对轮胎充气，在轮辋中心点处作用1/4整车载荷，进行加载仿真分析[16]。

4.1 轮胎加载后的位移分析

轮胎在加载1/4车重时的位移云图如图5所示。由图5可知，轮胎与地面的接触区域呈椭圆形，接触中心的形变量最小，如图5中的蓝色区域，轮胎接地椭圆区域两侧的形变量最大，如图5中的红色区域。

图5 轮胎加载位移Fig.5 Displacement of tire after loaded

4.2 轮胎加载后的应力分析

轮胎在加载1/4车重时的应力分布图如图6所示。由图6可知，受压区域的应力分布也呈椭圆状，在靠近胎肩部位出现了应力最大值。

图6 轮胎加载应力分布Fig.6 Mises distribution of tire after loaded

5 轮胎滑水性能影响因素分析

以水膜厚度、胎压、负载和沟槽深度4个因素作为控制变量，以临界滑水速度表征滑水性能，探究临界滑水速度随各因素的变化趋势。表3为不同仿真工况下的多组数据得到的轮胎临界滑水速度的仿真结果。

5.1 水膜厚度对轮胎滑水性能的影响

针对建立的光面胎和纵向花纹胎，如表3所示不同水膜厚度仿真工况下，轮胎临界滑水速度变化趋势如图7所示。

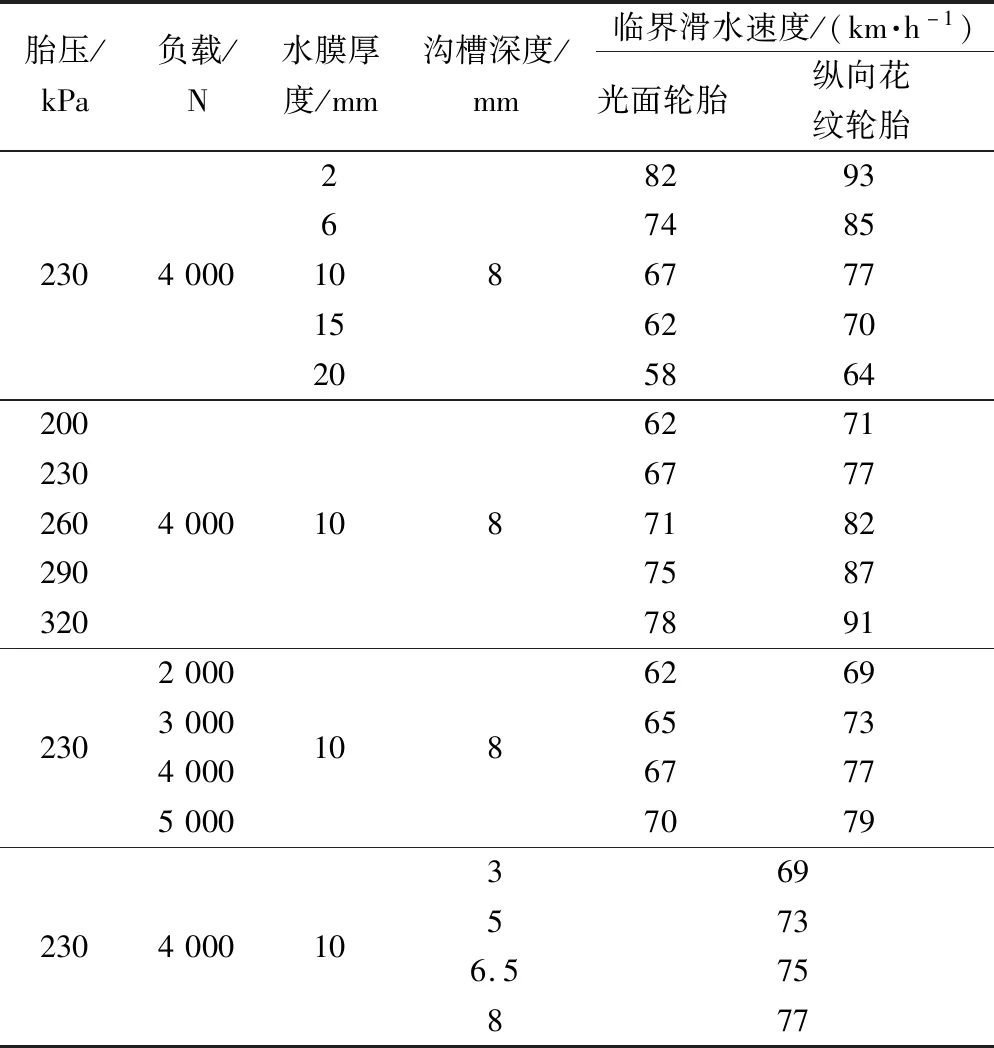
表3 不同仿真工况下临界滑水速度变化Table 3 The change of tire hydroplaning speed under different driving conditions

由图7可知，光面轮胎和纵向花纹轮胎的临界滑水速度都随水膜厚度的增加而减小，这是因为当路面上的水膜厚度增加时，轮胎与路面间的积水增加，随着轮胎的变形，积水不能及时从四周排出，水流会对轮胎产生动水压强，使轮胎的地面附着系数利用率减小。由于花纹的存在，纵向花纹轮胎与地面之间的积水能较多较快的从花纹沟槽中排出，增大了轮胎与地面的接触面积，使纵向花纹轮胎的临界滑水速度一直大于光面胎的临界滑水速度。所以，水膜厚度越大，汽车越容易出现打滑现象，增加了雨天行车的交通事故率，故可以通过改变路面的宏观弧度和微观粗糙度来减小雨天路面的积水深度，从而提高车辆的湿滑性能，保障行车安全。

图7 不同水膜厚度下轮胎临界滑水速度Fig.7 Tire hydroplaning speed under different water film thickness

5.2 充气压力对轮胎滑水性能的影响

不同充气压力仿真工况(表3)下，轮胎临界滑水速度变化趋势如图8所示。

由图8可知，光面轮胎和纵向花纹轮胎的临界滑水速度都随胎压的增加而变大，这是由于随着轮胎充气压力的增加，轮胎在加载行驶时变形会减小，轮胎的受压区域会变小同时轮胎的花纹沟槽会及时快速的排出积水。轮胎的沟槽为快速排水提供了条件，所以纵向花纹轮胎的临界滑水速度一直大于光面轮胎的临界滑水速度。因此在雨天行车时，要时时注意车辆的胎压情况，避免出现胎压小于标准胎压的情况出现，适当的增大胎压能提高轮胎的滑水性能。

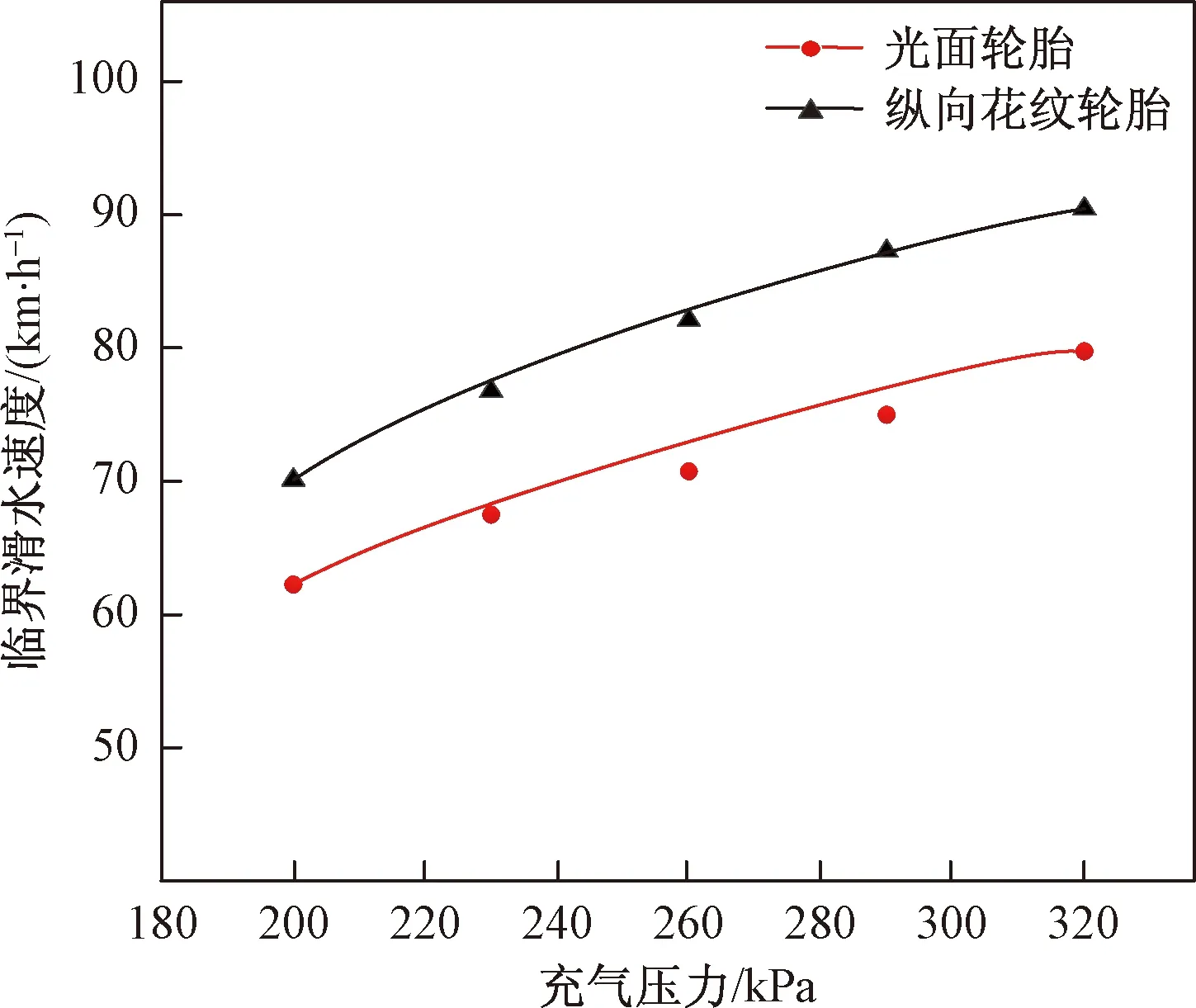
图8 不同充气压力轮胎临界滑水速度Fig.8 Tire hydroplaning speed under different pressure

5.3 轮胎负载对轮胎滑水性能的影响

不同轮胎负载仿真工况(表3)下，轮胎临界滑水速度变化趋势如图9所示。

由图9可知，光面轮胎和纵向花纹轮胎的临界滑水速度都随负载的增加呈上升的变化趋势，由于轮胎负载的增大，轮胎对地面的作用力变大，可以较快地把积水从轮胎与路面之间排出，并且水流的动水压力较晚的达到轮胎的负载，从而延缓滑水现象的出现。纵向花纹沟槽的存在可以更好地排出积水，所以在同一工况下纵向花纹轮胎比光面轮胎的临界滑水速度更高。

图9 不同轮胎负载轮胎临界滑水速度Fig.9 Tire hydroplaning speed under different loading

5.4 花纹沟槽深度对轮胎滑水性能的影响

轮胎的花纹结构设计对滑水性能的影响非常大。不同花纹沟槽深度仿真工况(表3)下，轮胎临界滑水速度变化趋势如图10所示。

图10 不同沟槽深度轮胎临界滑水速度Fig.10 Tire hydroplaning speed under different groove depth

由图10可知，纵向花纹轮胎的临界滑水速度随着沟槽深度的增加而变大。这是因为纵向花纹沟槽既可以排水也可以存水，减小轮胎受到的动水压力，延缓滑水现象的发生。所以当轮胎长时间使用后，花纹磨损严重，会降低轮胎的滑水性能，增加雨天事故的发生率。同时在轮胎花纹的研发设计过程中，在允许的范围内，适当增加花纹沟槽的深度可以提高轮胎的滑水性能。