隐性担保下债券定价的结构化模型及实证分析
2020-12-04徐承龙
赵 丹,徐承龙
(1. 同济大学数学科学学院,上海200092;2. 上海财经大学数学学院,上海200433)
随着国内金融市场的不断发展,企业选择发行债券进行融资,实现企业信息的充分披露,通过对公司信息的传递,可以有效降低信息不对称所造成的融资成本。如今我国企业债券数量不断增加,债券违约已经不仅局限于民营企业债券,截止2016年8月,国信债券市场已有41支债券违约,其中20支来自央企和地方国企,涉及金额164. 7亿元,占到了整体违约金额的65%,研究有违约风险的公司债定价变的越来越重要。同时观察到,政府对于国有企业债券的违约进行了兜底,这就可以看作政府对国有企业债券的隐性担保。政府隐性担保将政府与市场联系在一起,使得两者可以互补,出于保护国有资产、维持经济稳定或缓解地方财政困境等原因,一旦这些企业遭受违约危机,即使并未对其提供法律意义上的直接担保,但仍可能通过注入资本、财政补贴等方式对其进行某种意义的兜底。隐性担保可能会降低债券的违约风险,如何根据模型有效度量政府隐性担保,从而合理估计债券价格引起了越来越多学者的重视。
现有关于我国债券市场隐性担保的文献以经验研究居多。韩鹏飞等[1]利用债券二级市场上的交易数据发现政府隐性担保降低了国有企业债券投资者的风险,从而降低了信用利差,同时信用评级越低,对风险的降低效应越明显。钟辉勇等[2]分析了政府隐性担保对城投债的影响,结果显示有担保的债券和地方财政收入的增加利于提高债券评级,但对信用利差的降低无显著影响。罗荣华等[3]利用对比无担保城投债和有第三方担保城投债的数据分析了地方政府的隐性担保的效果,结果表明无担保城投债与第三方城投债在发行利差上无显著差异,这说明市场认为无担保城投债背后存在着市场的隐性担保且地方政府的财力会影响城投债的发行利差。汪莉等[4]通过理论和实证分析相结合的方式,研究了地方政府隐性担保对城投债发行利率的影响,分析了不同地区的影响程度,结果显示,经济较为发达的地区,政府具有较强的隐性担保能力,从而有利于降低债券利率和发行主体的融资成本。王博森等[5]采用约化模型估计出企业债中存在的隐性担保概率,发现AA 评级中央企业债和地方国有企业债的定价中,分别隐含着对应政府以39. 9% 和6. 7% 概率进行的隐性担保,而类似隐性担保在AA + 评级中央企业债和国有企业债定价中分别为33. 9% 和1. 2%。与既有文献的处理方法不同,本文采用结构化模型研究企业债券的隐性担保,能够进行定量分析且可以做反事实检验。
结构化模型肇始于Merton[6]基于期权定价理论所做的拓展研究,Black等[7]允许债券在到期日之前任意时刻均可以发生违约事件,引进了首次到达模型。利用此方法研究中国公司债定价问题的研究有解文增等[8],该文利用文献[6,9-10]结构化模型对中国市场债券的定价能力进行了分析,结果显示模型整体高估了公司债价格,且3个模型高估公司债价格的百分比逐渐减少,并提出适合中国公司债的结构化模型应降低低杠杆比率和低资产波动率公司债的价格,而提高高杠杆比率和高资产波动率公司债的价格。但该文并未考虑中国市场中普遍存在的政府隐性担保这一特色。
本文尝试将政府的隐性担保作用嵌入到债券定价的结构化模型中,并用债券价格进行定量分析。对于那些违约事件并未实际发生的公司发行的债券,采用模糊集的思想方法,将政府隐性担保概率作为重要参数加入到违约时刻的偿付中,得出适合中国市场实情的定价模型,并选取了2012 年第1 季度至2016 年第3 季度的季度公司债数据为研究样本,进行实证分析。首先,利用公司债价格的历史数据及债券发行主体特征数据等,对模型参数进行合理估计,针对国内市场中违约损失率缺乏历史数据的特点,采用了民企债数据结合最小二乘法进行估计。然后基于本文理论上推导出的含政府隐性担保的可违约债券价格公式,利用普通国企债和央企债的历史交易价格数据结合最小二乘法计算出不同类型企业债的政府隐性担保概率。最后,分析不同信用等级及不同地区的公司债券其政府隐性担保概率的差异性及其各自的特性。
本文主要贡献在于:①利用政府对民企债的政府隐性担保概率为0,在其他参数确定的情况下,通过最小二乘法对违约损失率进行了估计;②首次在债券定价的结构化模型中考虑了政府的隐性担保;③利用中国数据估算出了不同所有制下债券的政府隐性担保概率并对债券评级及地域因素进行了分析。研究结果表明,中央政府对央企债的隐性担保明显高于地方政府对地方国企债的隐性担保;债券评级越高的债券,政府隐性担保概率越高;经济水平发达的沿海地区,政府隐性担保概率更高。本文的研究发现有助于合理估计我国债券市场的价格,有利于投资者合理选择投资债券,具有一定理论和现实意义。
1 考虑隐性担保的可违约债券定价的结构化模型
假设某公司发行了期限为T 的零息债券,在到期日T 向持有者支付债券面值D0,与Merton[1]和Black等[4]中假设基本相同:
(1)市场是完全的,无套利的。
(2)公司资本结构由债务和股权组成,即公司只发行债券和股票。
(3)公司价值不受其资本结构的影响,即不考虑税收和破产成本。
(4)交易连续进行,没有交易成本,证券可以无限细分。
(5)在风险中性的假设下,公司资产价值Vt满足几何布朗运动

式中:r 表示无风险利率;δ 表示支出率;σ 表示公司资产的波动率;Wt表示标准布朗运动;t 表示时刻;r、δ、σ均为常数。
(6)债券可在到期日T 前违约,假设在τ̂时刻违约
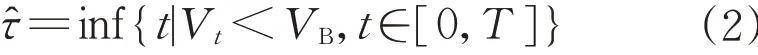
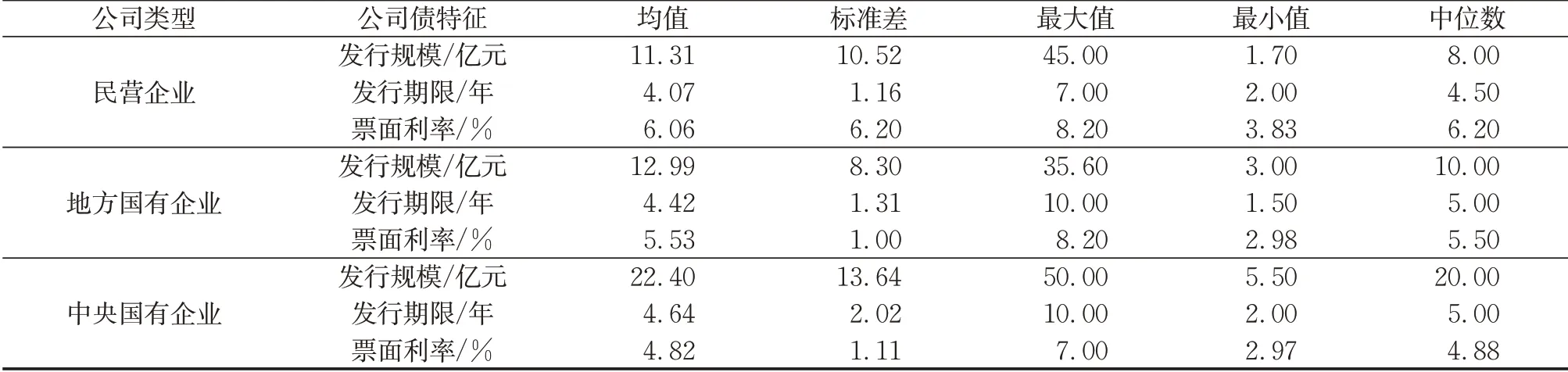
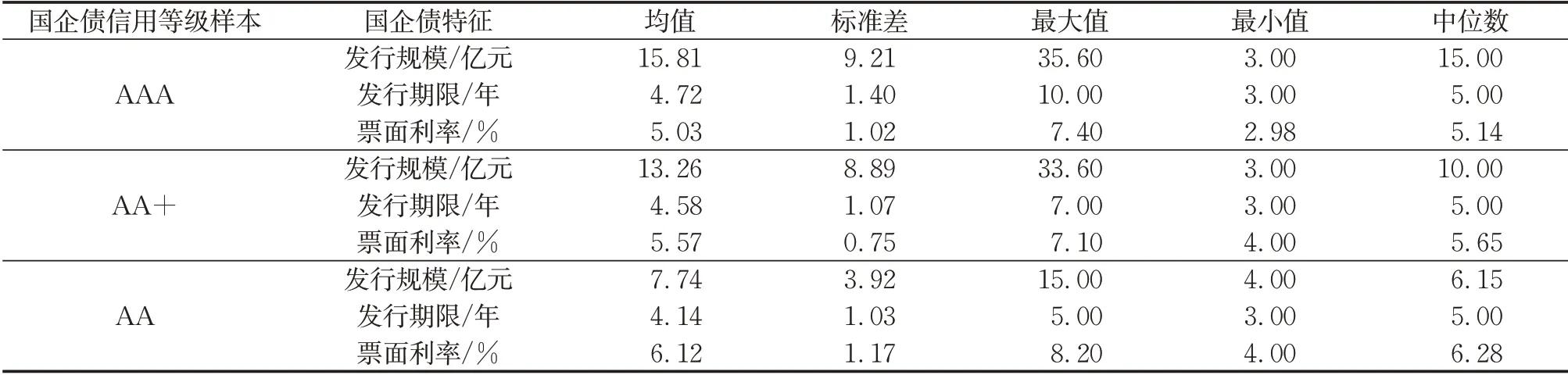
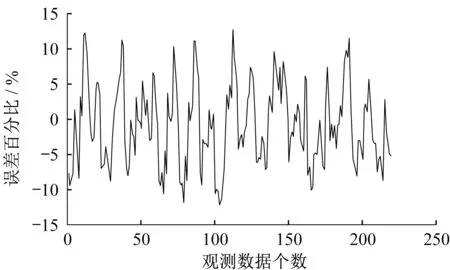
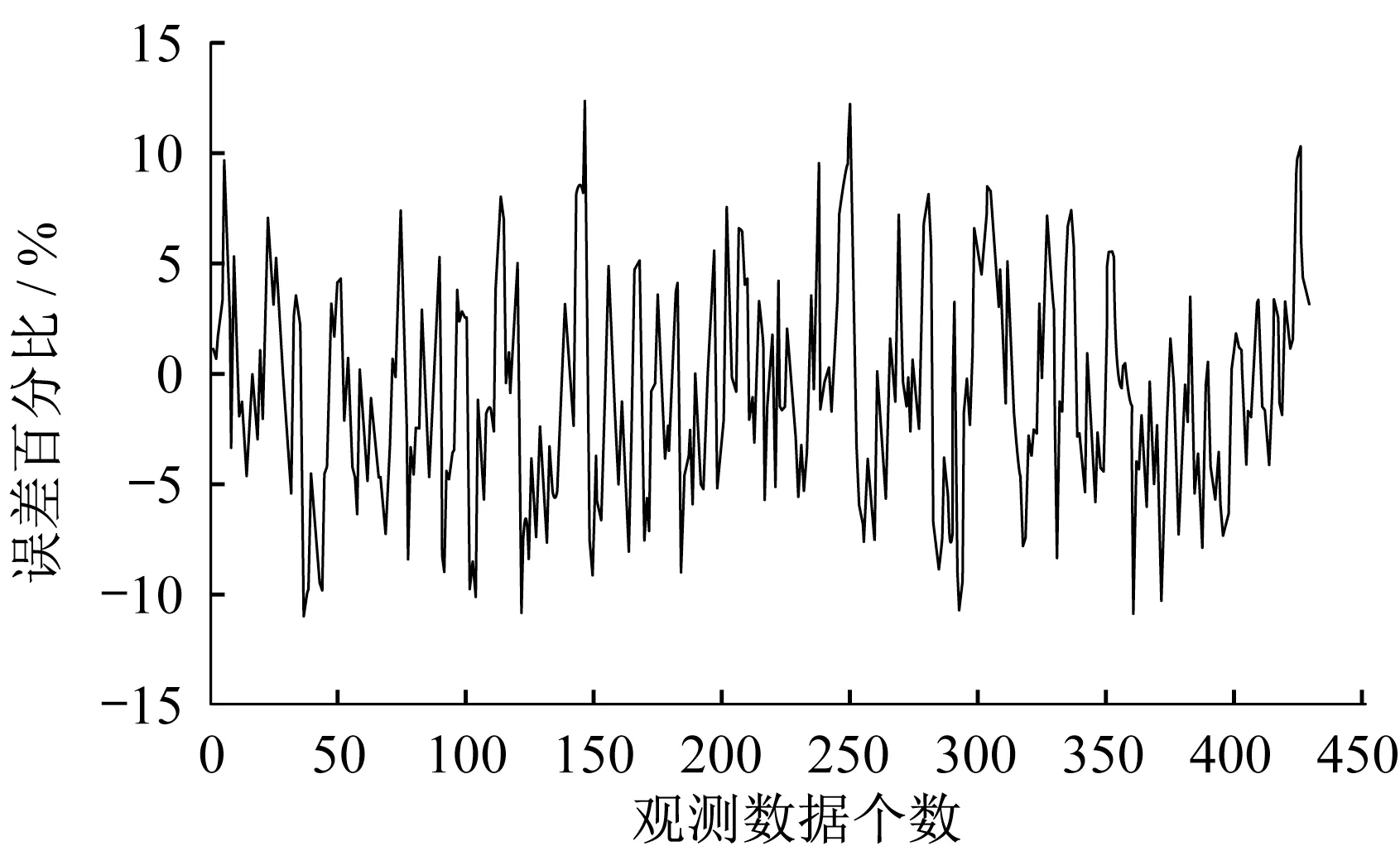
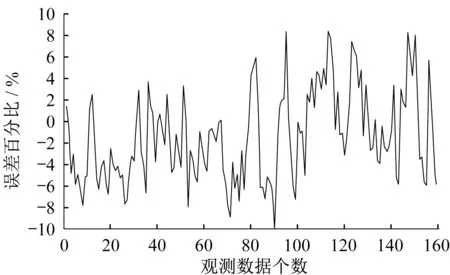
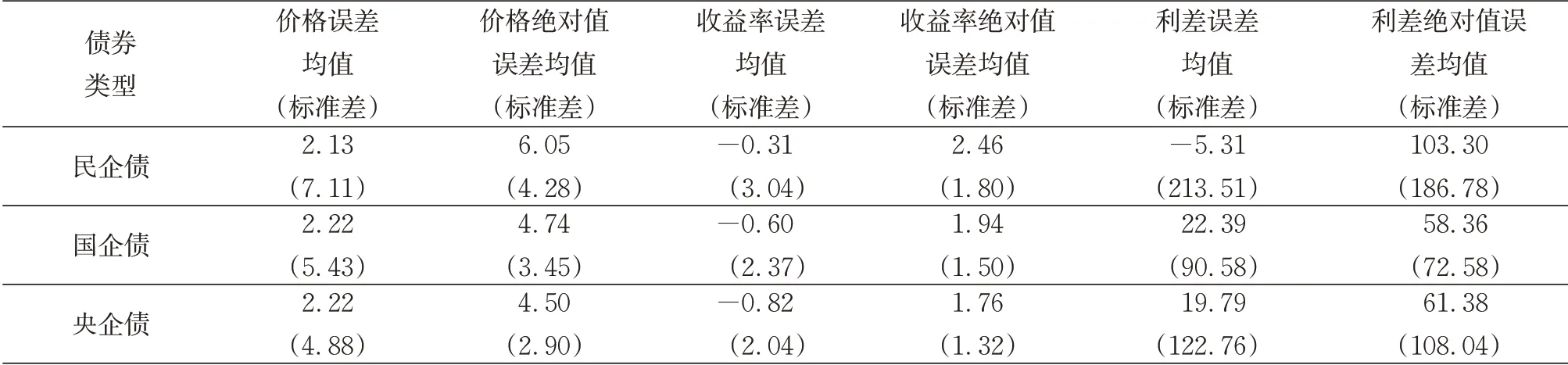
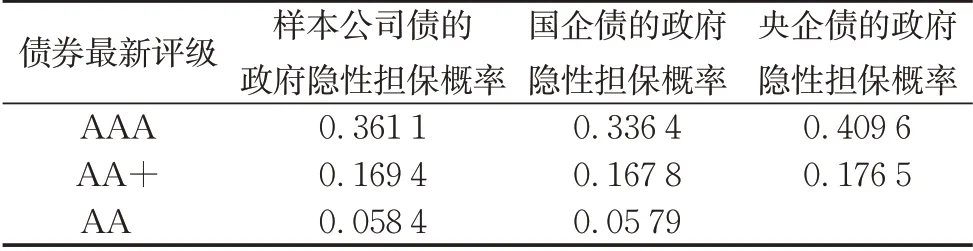
式中:VB为违约临界值,即一旦公司资产价值V (7)企业间存在政府的隐性担保问题,p 为政府隐性担保的概率,若公司发生违约,债券持有者拥有优先权,因而有p 的概率可以得到D0在违约时刻的贴现,有1−p的概率得到公司的全部清算后剩余资产(1−α )VB。 (8)直到债券到期日T公司未发生违约,持有者得到min {VT,D0}:即在到期日,若VT> D0,持有者将得到全部面值D0;若VT< D0,持有者将得到公司的全部资产VT。 引入完备带流概率空间( Ω,Gt,Q ),Q 为风险中性测度,市场全部信息组成的域流为G ={ Gt}t≥0,其中Gt为t时刻所有信息,违约时间τ̂是关于G的停时,即{ τ̂≤t }∈C。则对于债券持有者来说,含有违约风险的零息债券的价格在概率意义下可以表示为 不难发现e−rtPt是一个鞅,对e−rtPt用Itô公式,可得Pt= P(Vt,t )满足下列偏微分方程边值问题: 求解上述方程可得零息债券的价格: 式中: 由式(4)可以看出,前3项之和为不考虑政府隐性担保的情况下,可违约债券的结构化模型的定价公式,含有p的项为考虑政府隐性担保情况下所增加的部分。实证结果表明,与不考虑政府隐性担保的情况相比,在考虑了政府隐性担保的情况下所得的债券价格更高。 模型中参数有可直接观测部分与不可直接观测部分。可直接观测数据包括:公司债发行规模DS、公司总负债D0、债券息票c和其剩余到期时间τ。不可观测数据包括:公司的资产价值V、资产的波动率σ、支出率δ、无风险利率r、违约损失率α和政府的隐性担保概率p。不可观测部分可由可观测数据通过一系列计算近似估计,具体做法与Eom等[11]研究相似。最后再用最小二乘法利用交易数据对政府的隐性担保概率进行估算。 由于文章所求为零息债券价格,而样本债券均为付息债券,所以首先需要对样本债券的观测价格P̂进行处理,具体做法为:利用息票剥离的思想,将息票c以无风险利率r贴现至观测时刻t,观测价格P̂与息票的贴现价格差即为所需的对应零息债券在t时刻的近似观测价格~P,即 式中:tn,n= 1,2,…,[ T −t ]+ 1为从观测日开始至到期日的剩余付息日,其中[ T −t ]表示对剩余到期时间取整,本文所用样本公司债每年付票息1 次。例如,假设债券到期时间为5年,观测时刻为债券发行后的1. 2 年,则剩余付息次数为4 次,付息日分别为债券发行后第2、3、4、5年。 首先,将模型参数大致分为3类:第一类为公司债自身的特征变量,包括债券的剩余期限τ、票面利率c等,可直接得到;第二类为公司债发行主体的变量,包括公司的资产价值V、资产波动率σ、公司资产的支出率δ、公司债的发行规模DS及公司总负债D0等;第三类为其他变量,包括无风险利率r、违约边界VB及违约损失率α以及政府隐性担保概率p等。 V、σ和δ都是不可直接观测的。而D0可由公司的财务报表获得,可用公司的总负债与股票市值的和作为公司资产价值V的替代值。而由于国内市场的公司资本结构较为复杂,公司债发行规模只占了公司总债务的一部分,因此需要选取合适的公司资产进行债券价格计算,假设公司债发行规模为DS,则对应的公司资产为 在每个债券观测样本时刻t,计算之前150 个交易日公司股票收益的波动率作为资产波动率σ的代理变量,与文献[8]一致。资产支出率δ可以由公司的债券息票与分红的加权和估计,而由于国内公司分红率较低,因此本文用公司在债券息票的支出作为支出率的替代变量,具体做法为 在计算每只零息票债券时,选择与该债券剩余期限最接近的国债即期收益率作为无风险利率r 的代理变量,与文献[8]一致。令违约边界VB与公司总负债D0相等,即公司在资不抵债的时候发生违约。 而由于国内债券市场起步较晚,针对违约损失率的数据有所缺失,本文利用市场交易数据采用最小二乘法间接得到:收集民营企业、地方国有企业、中央国有企业的债券数据,由于政府对民营企业的担保概率为0,即p= 0。此时,在其他参数已确定的情况下,则可利用民企债数据通过最小二乘法确定违约损失率α,具体做法为 注意到式(6)中不含有待定参数p,直接在Y的表达式中对α求导,并令其导数值为0,可得 其中,Ai、Bi分别为每个观测价格处根据每个公司实际数据代入式(6)所得的A、B对应值。 模型中的参数估计方法和数据来源见表1。 表1 模型参数估计Tab. 1 Model parameter estimation 接下来,将计算出的α代入式(4)中,再分别利用普通国企债及央企债的数据结合最小二乘法思想计算出相应的政府担保概率p。 式中:Ci、Di分别为将第i个观测价格处的实际数据代入下式中计算所得的对应值: 本文公司债样本数据均来自于国泰安数据库,交易所国债即期收益率来自于Wind数据库,剩余期限在1~10年间,时间间隔为1年。选取2012年第1季度至2016年第3季度的季度公司债数据作为观测样本,令每个季度后的首月的月收盘价作为该季度的公司债观测数据,例如2013年10月的月收盘价作为2013年第3季度的季度收盘价观测样本。 为了能更好地满足模型假设条件,需要对选取的公司债样本数据进行筛选。首先,本文研究对象仅限于固定利率且不含权债券,故剔除浮动利率及累进利率债券,同时含有回售权或提前偿还条款的公司债也不满足本文研究范围,予以删除。其次,本文剔除掉发行主体不在A股上市的公司债样本。接着,类似Eom等[11]的做法,删除剩余期限不到1年的观测样本。最后,删除掉债券价格大于110和小于90的异常值数据。处理后,得到99家A股上市公司发行的116 支债券,共计805 个季度观测数据,其中27家民营企业的债券数据219个,54家国有企业的债券数据428个,18家中央国有企业的债券数据158个。 表2、表3 列举了全部及不同类型的公司债特征,包括债券的发行规模、发行期限及票面利率。根据债券发行期限不同,剩余期限在1 年至10 年属于中期债券,本文公司债属于中期公司债。对比表格中数据,可以发现:首先,民企债、国企债、央企债的发行规模呈递增趋势,而民企债的发行规模均值为11. 31 亿元,国企债发行规模均值为12. 99 亿元,央企债的发行规模均值为22. 40 亿元。这说明,一般来说,央企的偿债能力高于国企及民企,且央企规模较大相应的所需资金规模大,因此,公司债的发行规模也大。其次,3 种类型债券的发行期限也在递增,其中民企债的平均发行期限为4. 07年,国企债的平均发行期限为4. 42 年,央企债的平均发行期限为4. 64 年。这说明,央企相较于国企和民企发行的债券到期时间更长,这与Barclay 等[12]实证结果相一致,规模大的公司具有更多的长期债务。最后,3 种类型债券的票面利率呈减趋势,其中,民企债平均发行的票面利率6. 06%,国企债平均发行的票面利率为5. 53%,央企债平均发行的票面利率为4. 82%。这一结果说明,违约风险小的债券其票面利率也相应较低,央企相对于国企及民企,违约概率较低,其相应的回报率也低。 表2 公司债样本数量统计Tab. 2 Number of corporate bond samples 表3 公司债样本特征统计Tab. 3 Characteristics of corporate bond samples 此外,表4、表5 分别列举了不同信用等级的国企债和央企债统计特征。从表3、表4 看出,信用等级越低,债券的发行规模及发行期限越低,而票面利率逐渐变大。一般来说,公司债的信用评级高,公司的经济实力较好,相应所需的资金也更大,因此债券的发行规模较大。Guedes 等[13]实证结果表明,公司规模越大,债券等级越高的公司更倾向于发行期限长的债券,因此债券的发行期限越大。而由于信用评级高,公司债的违约风险小,投资者所承担的风险也越低,因此票面利率越低。 表4 不同信用等级的国企债特征统计Tab. 4 Characteristics of state-owned enterprise bond samples at different credit ratings 比较表4和表5,相同信用评级的国企债和央企债,发行规模及发行期限变大,票面利率变低,与表3结果一致。 本节采用中国公司债交易数据,利用第2 节提出的定价公式对国企债和央企债的政府隐性担保概率进行估计分析。首先,利用民企债交易数据利用式(7)求得市场中所缺乏的违约损失率数据。接着,利用式(8)求得不同类型债券的政府隐性担保概率,并估计模型的预测误差,包括价格、收益率及公司债利差的误差。其中,本文定义的价格误差等于模型的理论价格减去实际观测到的价格,然后除以实际观察价格,收益率与利差的误差与价格误差定义类似。最后,分析不同债券的信用评级及地区差异性对政府隐性担保概率的影响。 表5 不同信用等级的央企债特征统计Tab. 5 Characteristics of central-owned enterprise bond samples at different credit ratings 首先,由于政府对民营企业不存在担保,因此对民企债而言,政府隐性担保概率p= 0,在其他参数确定的情况下,利用民企债交易数据通过式(7)计算得到回收率α= 0.2218,残差见图1。 图1 违约损失率α=0.221 8时民企债价格残差图Fig. 1 Residual values of private enterprise bond prices at α=0.221 8 然后将α= 0.221 8 代入进国企债价格式(4)中,此时,其他参数都已确定,通过式(8)计算得到国企债的政府隐性担保的概率为p= 0.208 2,此时所得残差见图2。 同理可以得到央企债的政府隐性担保的概率为p= 0.322 9,残差见图3。 图2 国企债的政府隐性担保概率p=0.208 2时债券价格残差图Fig. 2 Residual values of state-owned enterprise bond prices at p=0.208 2 图3 央企债的政府隐性担保概率p=0.322 9时债券价格残差图Fig. 3 Residual values of central-owned enterprise bond prices at p=0.322 9 由图1至图3可知,残差控制在10%以内,说明模型拟合公司债的市场价格能力可信。此时,所得残差平方和最小的违约损失率为α= 0.221 8,将其代入式(8),根据国企债和央企债的交易数据得到国企债和央企债的政府隐性担保概率分别为20.82%和32.29%,此时隐性担保概率不为0,说明我国债券市场上存在政府的隐性担保,且央企债的政府隐性担保概率大于国企债的政府隐性担保概率。债权人认为当公司债发生违约时,政府对央企债的兜底概率较国企债大。这是由于中央国有企业处于国家安全和国民经济命脉的主要行业中,其经营管理大部分受制于政府,政府对其债务兜底的意愿相对于地方国有企业更强,因此央企债的政府隐性担保概率更高。同时,由于中央政府的财力相较于地方政府更好,对债务的兜底能力更强,而这种担保能力也会影响到其担保意愿,因此两方作用使得央企债的政府隐性担保概率更高。 表6展示了模型对全部公司债观测样本的定价误差。结果显示,模型高估了公司债的价格,低估了公司债的收益率,低估了民企债的利差:平均高估民企债价格约2. 13%,收益率的误差为−0. 31%,利差的误差为−5. 31%,这说明对违约回收率的计算具有可信度。同时模型高估国企债价格2. 22%,低估其收益率−0. 60%,高估其利差22. 39%,高估央企债价格国企债价格2. 22%,低估其收益率−0. 82%,高估其利差19. 79%,可以看出将政府隐性担保考虑进模型会使债券利差变大,产生误差的原因可能是中国公司债的流动性差,对公司利差产生了显著影响。 表6 模型定价结果分析Tab. 6 Result analysis of pricing model % 按债券评级进行进一步分析,由于数据量及民企债信用评级大部分为AA+和AA,此处假设企业违约损失率大致相同,直接将α= 0.221 8 代入计算。首先,将国企债和央企债分别按信用评级进行分类,得到AAA级国企债数据197个,AA+级国企债数据136 个,AA 级国企债数据108 个;AAA 级央企债数据97 个,AA+级国企债数据29 个。将不同类型及信用等级的债券数据代入式(8)计算出政府隐性担保概率,结果见表7。 由表7可知,债券评级不同,政府隐性担保概率也不同:政府对AAA级债券的政府隐性担保概率为36. 11%,对AA+级债券的政府隐性担保概率为16. 94%,对AA 级债券的政府隐性担保概率为5. 84%。可以看出,政府对信用评级越高的债券,存在隐性担保的可能性越大。这就是说,站在债权人的角度,信用评级越高,受政府担保的可能性就越大,政府为其提供道德上财务救助的可能性也越大,相应的债券的违约风险也会越小。 同时,AAA 级债券中,央企债的政府隐性担保概率为40. 96%,普通国企债的政府隐性担保概率为33. 64%,AA+级债券中,央企债的政府隐性担保概率为17. 65%,普通国企债的政府隐性担保概率为16. 78%。由此看出,对于相同信用评级的债券来讲,央企债的政府隐性担保概率高于普通国企债的政府隐性担保概率,对于同类型债券来说,债券评级越高,政府隐性担保概率越高。 表7 按信用等级分类的政府隐性担保概率Tab. 7 Probability of government implicit guarantee at different credit ratings 分析地区不同的情况下,政府隐性担保概率的变化。选取公司所在地分别为东三省(黑龙江、吉林、辽宁)和江浙沪(江苏、浙江、上海)的公司债数据进行比较分析。由于主要研究地区对公司债政府隐性担保概率的影响,故选用信用等级相近(AAA 级和AA+级)的国企债和央企债总数据进行计算。结果见表8。 由表8 可知,所在地为东三省的公司债政府隐性担保概率为19. 72%,而公司所在地为江浙沪的公司债政府隐性担保概率为31. 49%。这说明政府隐性担保存在地区差异,经济发达地区的公司债的政府隐性担保概率较高,而经济不发达地区的公司债的政府隐性担保概率相对较低。因为对于地方政府而言,政府的财力状况会影响政府的担保能力,2016年黑龙江地方财政收入为1 148. 4亿元,而上海的地方财政收入为6 406. 1 亿元。这说明政府的财力状况越好,其担保能力就越强,当债券面临违约风险时,政府可以提供相对好的财力进行兜底偿付,从而经济发达地区公司债的政府隐性担保概率更大。 表8 按地区分类的政府隐性担保概率Tab. 8 Probability of government implicit guarantee in different regions 本文从理论模型和实证两方面研究了中国政府对公司的隐性担保问题。在理论模型方面,首次提出基于政府隐性担保的结构化违约模型:将政府隐性担保作为概率常数加入债券定价的结构化模型中,再利用偏微分方程方法求解得到了适合中国债券市场的债券价格的解析表达式。 基于此定价公式,可进一步对含有政府隐性担保的债券进行理论分析。 在实证方面,首先对模型参数进行估计,由于国内债券市场对违约损失率的缺失,本文首先利用民企债数据对国内违约损失率数据进行估计。接着利用国企债和央企债样本数据,对政府隐性担保概率进行了实证分析:①分别对国企债和央企债的政府隐性担保概率进行了估计,发现政府对国企债的政府隐性担保概率为20.82%,对央企债的政府隐性担保概率为32.29%;②根据债券评级不同对债券的政府隐性担保概率进行了估计,债券评级越高的债券,政府隐性担保概率越高;③对不同地区的债券进行了分类分析,发现与内地相比,经济水平发达的沿海地区,政府隐性担保概率更高。 研究结果对于中国特色债券市场的价格分析有重要意义,同时有助于投资者对于债券风险进行合理估计。需要说明的是由于本文计算的违约损失率以及政府的隐形担保概率的大小只是根据公司的类型、信用等级大小以及区域等粗略划分的,因此如何更精确、科学地对不同的公司债券进行特征分析是笔者下一步的研究任务。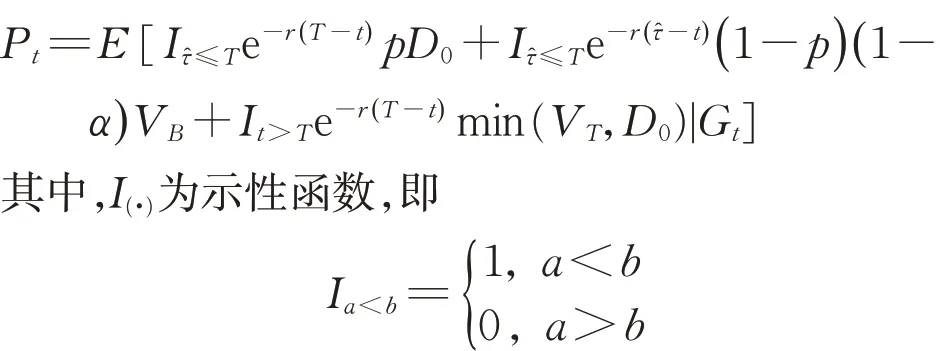
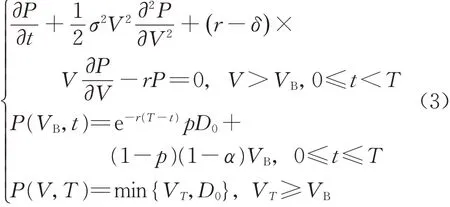
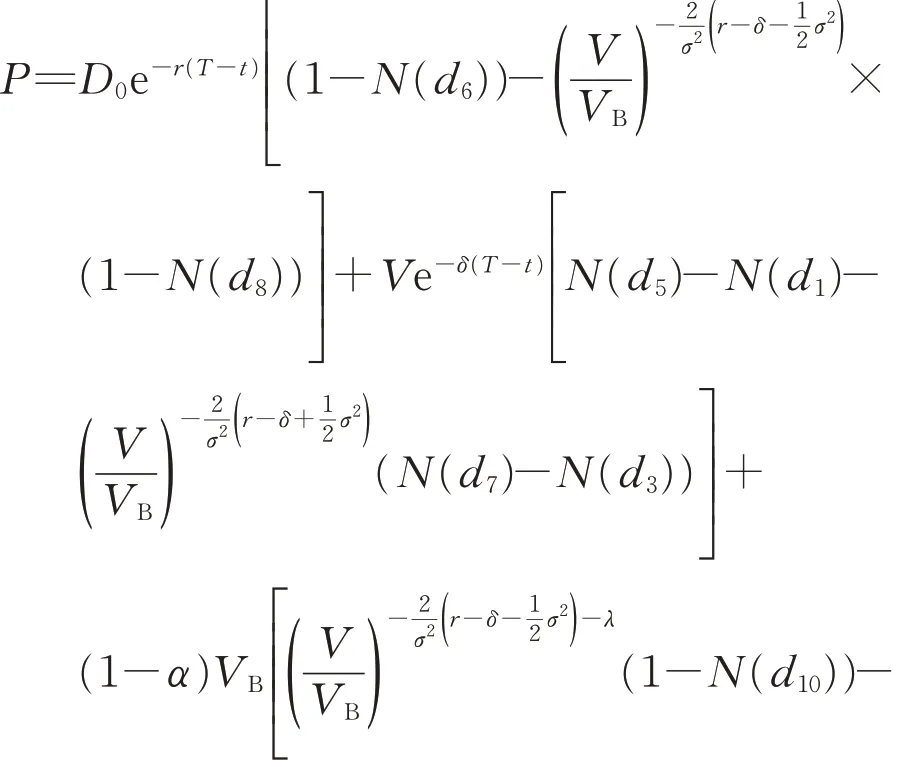
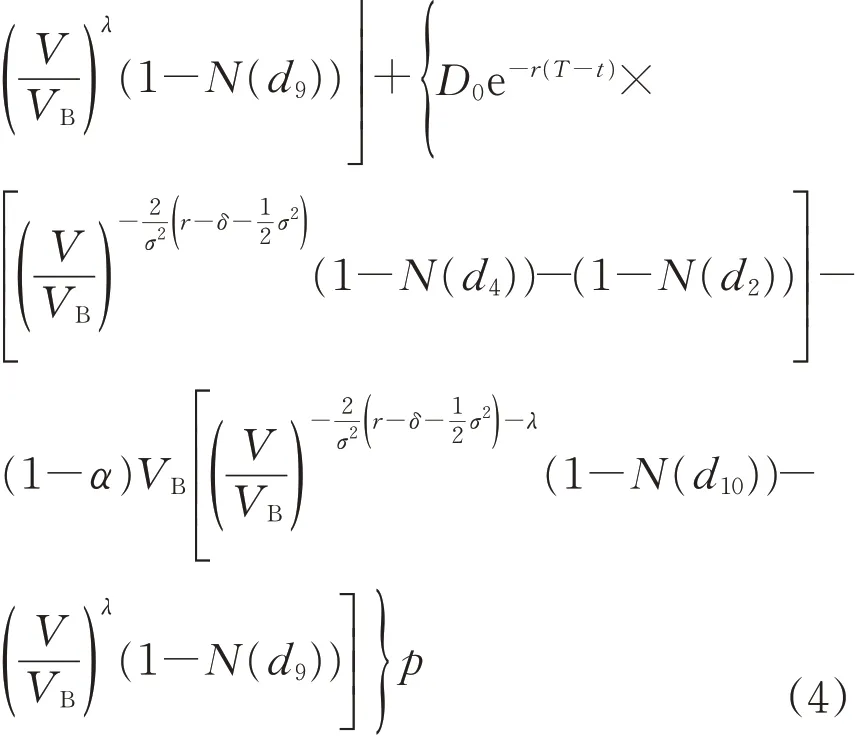
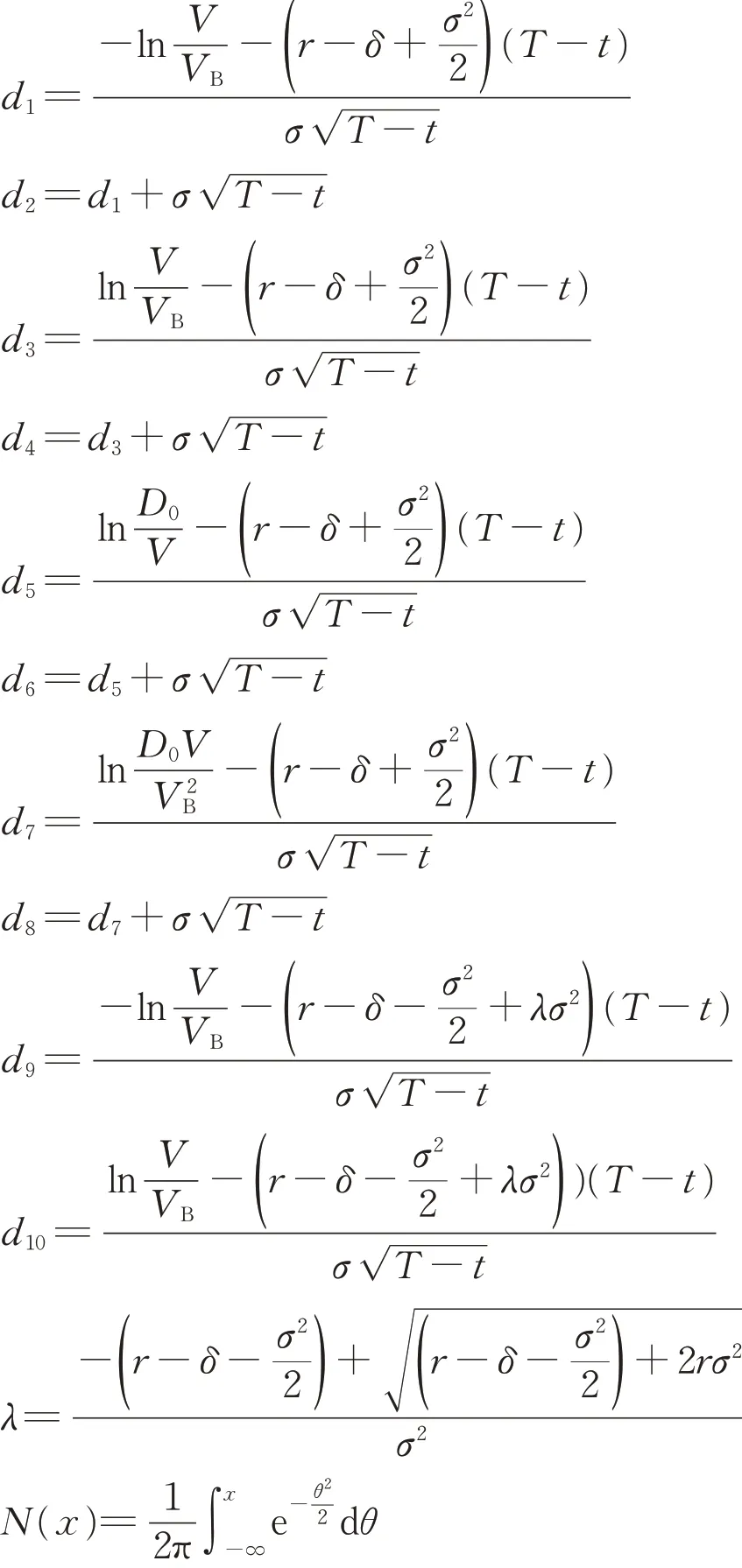
2 模型参数处理及估计方法

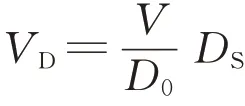
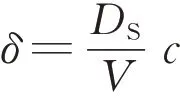
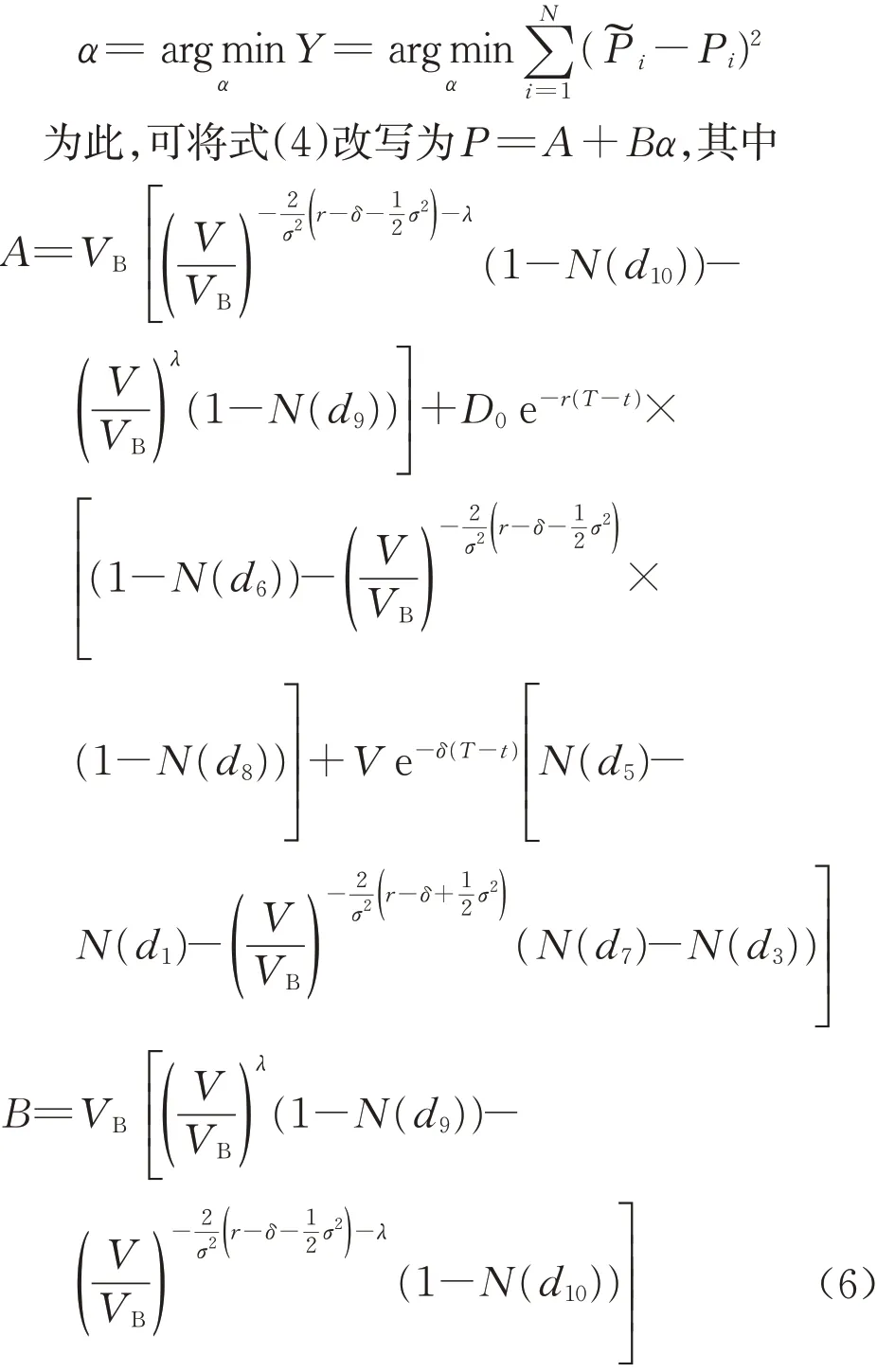




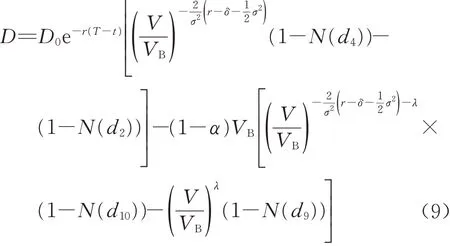
3 数据说明

4 实证结果及分析


5 结论
