求解一类隐式互补问题的加速模系矩阵分裂迭代法
2020-12-04殷俊锋
殷俊锋,丁 戬,李 蕊
(1. 同济大学数学科学学院,上海200092;2. 嘉兴学院数理与信息工程学院,浙江嘉兴314001)
1 背景介绍
互补问题广泛地出现在科学和工程的许多应用中,如弹性接触、经济运输、流体动力学的边界问题、凸二次规划以及反问题等[1],因此受到越来越多研究者的关注和研究,并已经取得了丰硕的成果。本文考虑如下一类隐式互补问题[2]:求向量u和r∈Rn满足

式中:M∈Rn×n为给定矩阵;q=(q1,q2,…,qn) ∈Rn为给定实向量;f为Rn到它本身的一个映射。特别地,当函数f= 0,问题(1)化为线性互补问题[3]。
针对线性互补问题,白中治[4]提出了模系矩阵分裂迭代法,并对系数矩阵为正定或H+‐矩阵下迭代法的收敛性进行了分析。由于模系矩阵分裂迭代算法格式简单且收敛速度较快,该方法吸引了众多学者的关注并得到了进一步的研究。如两步模系矩阵分裂迭代法[5]、广义模系矩阵分裂迭代法[6]和松弛模系矩阵分裂迭代法[7]等。为了更快速有效地求解大型稀疏线性互补问题,白中治等[8]通过引进并行计算技术,构造了模系矩阵同步多分裂迭代法,并建立了此算法在系数矩阵为H+‐矩阵时的收敛性分析。夏泽晨等[9]首次构造了求解非线性互补问题的模系矩阵分裂迭代法,进一步地还有两步模系矩阵分裂迭代法[10-12]、松弛模系矩阵分裂迭代法[13]以及加速模系矩阵分裂迭代法[14-15]等也相继被构造。
李郴良等[16-17]构造求解隐式互补问题(1)的模系矩阵分裂迭代法和模系矩阵同步多分裂迭代法,并建立了当系数矩阵为正定或H+‐矩阵时迭代法的收敛性质。曹阳等[18]对文献[16]中的模系矩阵分裂迭代法的收敛理论给出了更加完整的证明。王艳等[19]采用两步模系矩阵分裂迭代法对隐式互补问题(1)进行求解,并且分析了系数矩阵为H+‐矩阵时算法的收敛性。曹阳等[20]同样构造了两步模系矩阵分裂迭代法求解隐式互补问题(1)并且建立了迭代法在系数矩阵为正定或H+‐矩阵时迭代法的收敛性质。
郑宁等[21-22]通过对向量边计算边更替的思想,将线性互补问题转换成了新的隐式不动点方程,提出了加速模系矩阵分裂迭代法求解线性互补问题,并从理论上分析了算法在系数矩阵为正定或H+‐矩阵时的收敛性质。通过选择合适的系数矩阵,该方法也可以得到文献[4]中的传统模系矩阵分裂迭代法。为了进一步加快求解隐式互补问题的收敛速度,本文引入对向量边计算边更替的思想,提出了加速模系矩阵分裂迭代法。理论分析建立了新方法在系数矩阵为H+‐矩阵时的收敛性质。数值实验表明所提方法是有效的,并在迭代步数和时间上均优于传统的模系矩阵分裂迭代法。
2 加速模系矩阵分裂迭代法
先给出本文讨论中使用的一些记号及基本概念。
给定两个实矩阵M =(mij),N =(nij) ∈Rm×n,如 果 对 任 意 的1≤i≤m,1≤j ≤n 都 有mij≥nij(mij> nij),则记M ≥N (M > N)。本文,用记号| M | =(| mij|) ∈Rm×n表示M的绝对值。
令M ∈Rn×n为一个实n× n 矩阵,它的比较矩阵M =( mij)定义为

若对任意i≠j,有mij≤0,则称M为Z‐矩阵。若M为非奇异的Z‐矩阵且M−1≥O,其中O为零矩阵,则称M为M‐矩阵。如果M 为M‐矩阵,则称M为H‐矩阵。对于H‐矩阵M,有M 非奇异且| M−1| ≤M−1。特别地,对角元为正的H‐矩阵称为H+‐矩阵。
给定M ∈Rn×n,设M = F −G,如果F非奇异,则称M = F −G为矩阵M的一个分裂;如果F是非奇异的M‐矩阵并且G ≥0,则称该分裂为M‐分裂;当F −|G|是一个M‐矩阵,则称M = F −G是一个H‐分裂;如果M = F −| G |,则称此分裂为H‐相容分裂。

的等价不动点方程,其对于建立加速模系矩阵分裂迭代算法是至关重要的。
定理1[16]令M = F −G 为矩阵M 的一个分裂,给定初始向量x(0),对于隐式互补问题(1),下列结论成立:

是隐式互补问题(1)的解。
基于隐式不动点方程(2),李郴良等[16]构造了如下求解隐式互补问题的模系矩阵分裂迭代法。
算法1 (模系矩阵分裂迭代法)
步骤1 定义U ={ u:u−f ( u)≥0,Mu+ q≥0 },令M = F −G为矩阵M的一个分裂。
步骤2 给定ε > 0,u(0)∈U,k = 0。
步骤3 计算解:
1)计算初始向量
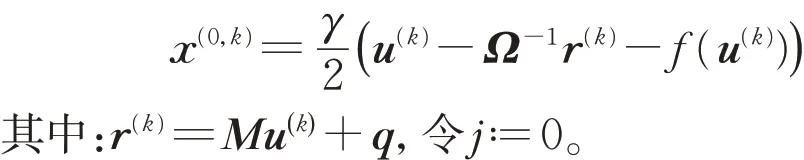
2)通过下列迭代格式计算x(j+1,k):
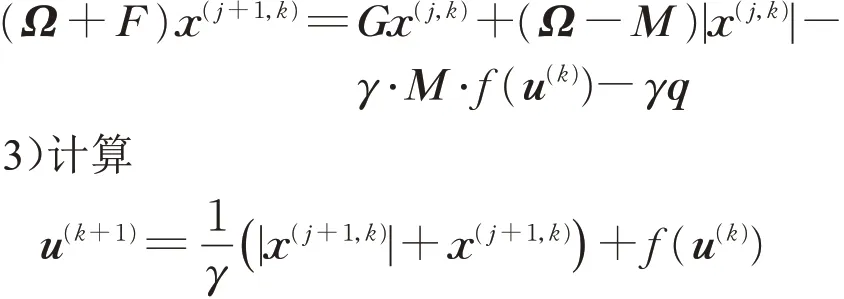
步骤4 如果u(k+1)满足停止准则,则迭代停止。否则,令k = k + 1且转向步骤2。
为了加快求解隐式互补问题的传统模系矩阵分裂迭代法的收敛速度,通过引入对向量边计算边更替的思想,可构造如下加速模系矩阵分裂迭代法。
算法2 (加速模系矩阵分裂迭代法)
步骤1 定义U ={ u:u−f ( u)≥0,Mu+ q≥0 },令M = F1−G1= F2−G2为 矩 阵M 的 两 个分裂。
步骤2 给定ε > 0,u(0)∈U,k = 0。
步骤3 计算解u(k+1):
1)计算初始向量

步骤4 如果u(k+1)满足停止准则,则迭代停止;否则,令k = k + 1且转向步骤2。
3 收敛性分析
本节建立了系数矩阵为H+‐矩阵情况下加速模系矩阵分裂迭代法求解隐式互补问题(1)的收敛性分析。
引理1[23]令M ∈Rn×n是一个H+‐矩阵,则|M−1|≤M−1。
引理2[24]令M ∈Rn×n,则ρ( M )< 1当且仅当
由定理1知,若(u*,r*)为隐式互补问题(1)的解,则
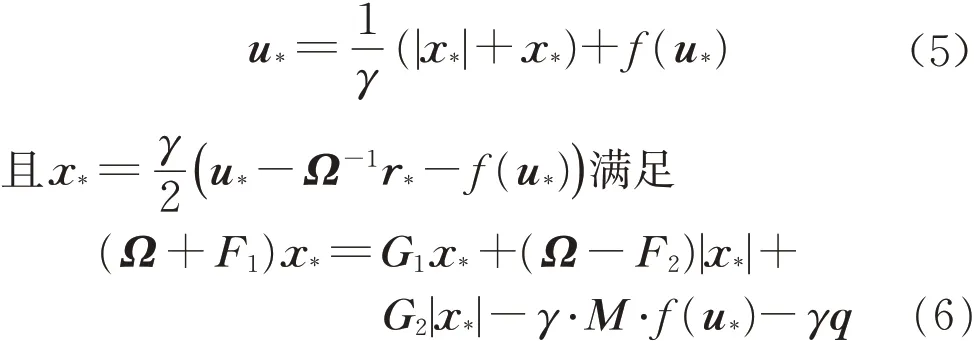
定理2 令矩阵M ∈Rn×n为H+‐矩阵,M =F1−G1= F2−G2为矩阵M的两个H‐相容分裂。假设Ω ∈Rn×n为一个正对角矩阵,γ是一个正常数,且f (u)是一个李普希兹连续函数,即存在非负矩阵N满足|f ( u)−f ( v )|≤N|u−v|,∀u,v ∈Rn,定义

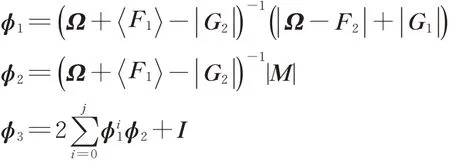
如果Ω ≥diag (F2)且Ω + F1−| G2|是一个M‐矩阵及

因为M = F1−G1= F2−G2是矩阵M 的两个H‐相容分裂,则
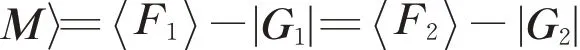
由M是H+‐矩阵可得F1为H+‐矩阵,且由引理1知

类似地,式(3)减去式(6),且两边同时加上绝对值得
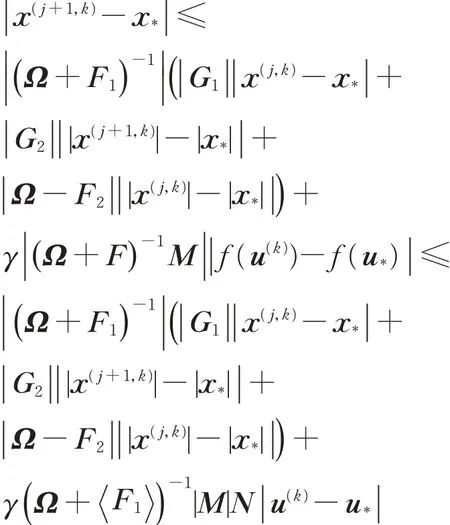
或者等价的有
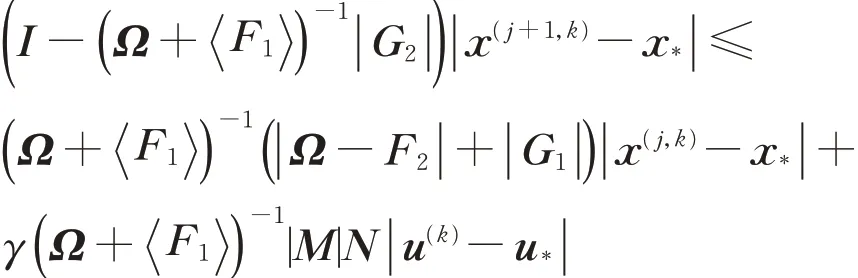
因为Ω + F1−| G2|为M‐矩阵,则Ω + F1也为M‐矩阵。 因此Ω + F1−| G2|是M‐分裂,且

进一步知I −(Ω + F1)−1| G2|为M‐矩阵,且其逆为非负矩阵,从而
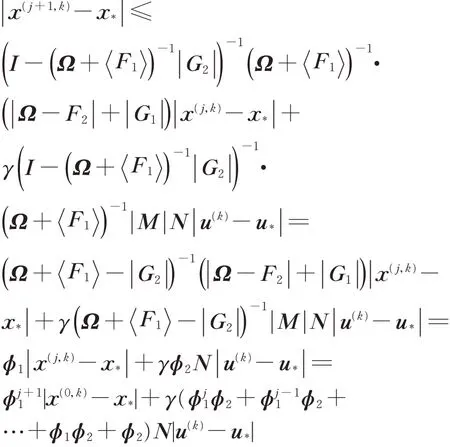
类似可得
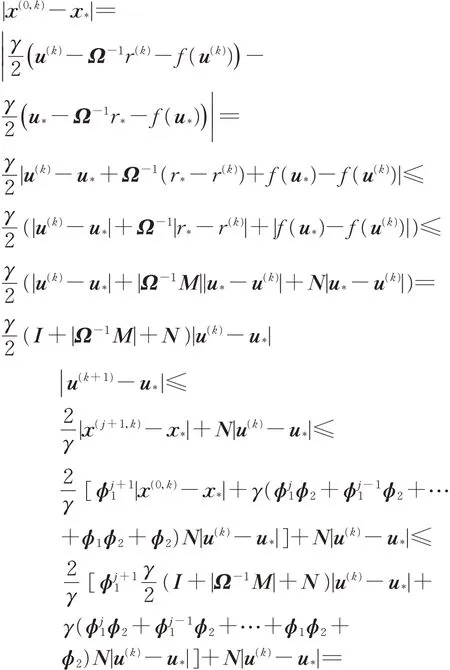

定义Ẑ= ϕj1+1( I +|Ω−1M|+ N )+ ϕ3N,则式(7)可以表示为

显然,如果ρ( Ẑ)< 1,迭代序列{ u(k)}∞k=0收敛到u*。事实上
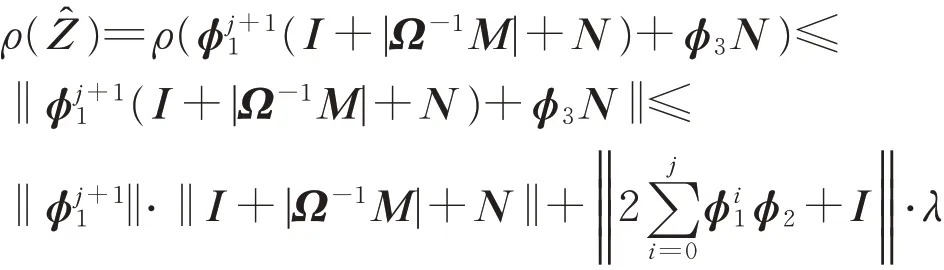
由文献[21]可知当M = F1−G1= F2−G2为矩阵M 的两个H‐相容分裂,且Ω + F1−| G2|是一 个M 阵 时,可 得ρ(ϕ1)< 1。 由 引 理2 可 得= 0。故存在一个正整数j0,当j ≥j0时有
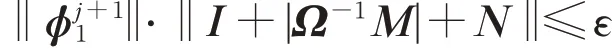
于是,对于∀j ≥j0有

类似地,可以建立下列加速的模系矩阵加速超松弛迭代法的收敛理论。
推论1 设矩阵M 为H+‐矩阵,令M=D−L−U=D−B,这里D、−L和−U分别是矩阵M的对角部分,严格下三角部分及严格上三角部分。 假设Ω为一个正对角矩阵满足Ω ≥D,γ 是一个正常数,若为M‐矩阵,松弛系数α 和β 满足下列条件:
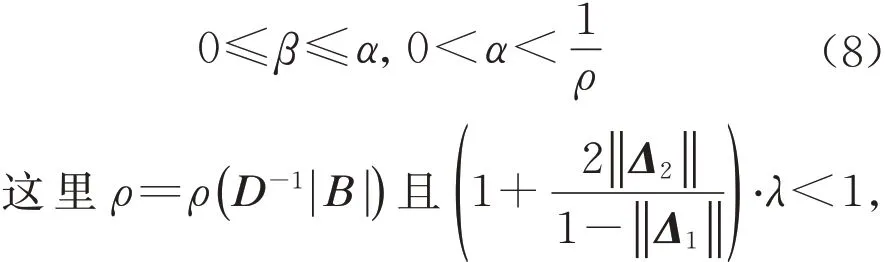
其中λ同定理2中定义。

则任意给定初始向量u(0)∈U,算法2生成的迭代序列{ u(k)}∞k=0收敛到隐式互补问题(1)的唯一解u*。

用式(10)减去式(9),可得

由条件可知Ω ≥D且0≤β ≤α,在式(11)两边同时加上绝对值可得

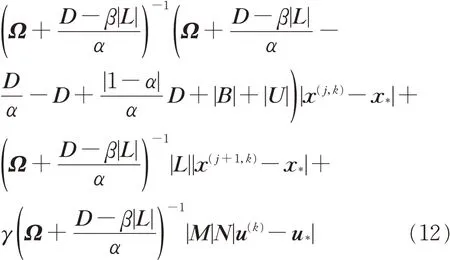
式(12)等价于


与定理2类似可得

由文献[21]可知,当α、β满足条件(8)时,有ρ(Δ1)<1。由引理2 可得jl→im∞Δj1+1= 0。故存在一个正整数j0,当j≥j0时

4 数值实验
本节将给出一些数值算例来验证加速模系矩阵分裂迭代法的有效性。数值实验将从迭代步数(IT)、所消耗时间(CPU)和残差范数(RES)3 个方面来反映算法的优劣。其中残差范数定义为
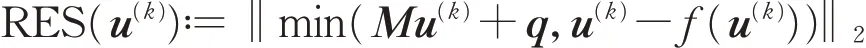
所有计算均在一台CPU 为1. 8 GHz 和内存为8 GB 的机器上运行,编程语言为MATLAB。在本实验中,所有的初始向量取为:u(0)=(0,0,…,0,0,…)T∈Rn. 并且内迭代的停止准则为‖x(j+1,k)−x(j,k)‖≤10−4,外 迭 代 的 停 止 准 则 为RES(u(k))≤10−6。α为加速模系矩阵逐步超松弛迭代法与模系矩阵逐步超松弛迭代法的迭代系数,最优参数为使得这两种迭代法迭代步数与时间最小的参数。
例1 设m为给定的正整数,n=m2。在式(1)中取M=M̂+μI,q=−Mz⋆,其中

为块三对角矩阵,其中S=tridiag(−1. 5,4,−0. 5)∈Rm×m为三对角矩阵,取z⋆=(1,2,1,2,…,1,2,…)T∈Rn和f(u)=(arctan(u1),…,arctan(un))。
例2 设m为给定的正整数,n=m2。在式(1)中取M=M̂+μI,q=−Mz⋆其中

为块三对角矩阵,其中S=tridiag(−1,4,−1)∈Rm×m为三对角矩阵,取z⋆=(1,2,1,2,…,1,2,
表1列出了例1和例2中使用的6种测试方法及其缩写符号。表2 列出了μ= 2,α以0. 2 为间隔从1. 0 到2. 2 变化以及矩阵维数增加时,MSOR 及AMSOR算法迭代步数与迭代时间的数值结果。

表1 测试方法及其缩写Tab. 1 Abbreviations of testing methods
从表2 中可以看到当μ= 2,矩阵维数为400、1 600、3 600 和6 400 时,从最小化迭代时间考虑,MSOR 相对应的最优参数分别为2. 0、2. 0、2. 0 和1. 8,然而AMSOR 的最优参数分别为1. 8、1. 6、1. 6和1. 4。
表3和表4中列出了当μ分别为2和4,矩阵维数增加时在最优参数下6 种方法的迭代步数、迭代时间以及残差范数的比较结果。

表3 例1中最优参数下6种方法的数值结果(μ=2)Tab. 3 Numerical results for six methods with optimal parameters for example 1(μ=2)

表2 例1中当α变化时MSOR和AMSOR的迭代步数与时间(μ=2)Tab. 2 IT and CPU for MSOR and AMSOR with the change in α for example 1(μ=2)

表4 例1中最优参数下6种方法的数值结果(μ=4)Tab. 4 Numerical results for six methods with optimal parameters for example 1(μ=4)
从表3 和图1 中可以看到所有的方法都快速收敛,并且所有迭代法的迭代时间随着矩阵维数的增加而增加。测试的6种算法中AMSOR 需要最少的迭代步数与时间,并且所有的加速模系矩阵分裂迭代法与相对应的模系矩阵分裂迭代法相比迭代步数与迭代时间都更少。
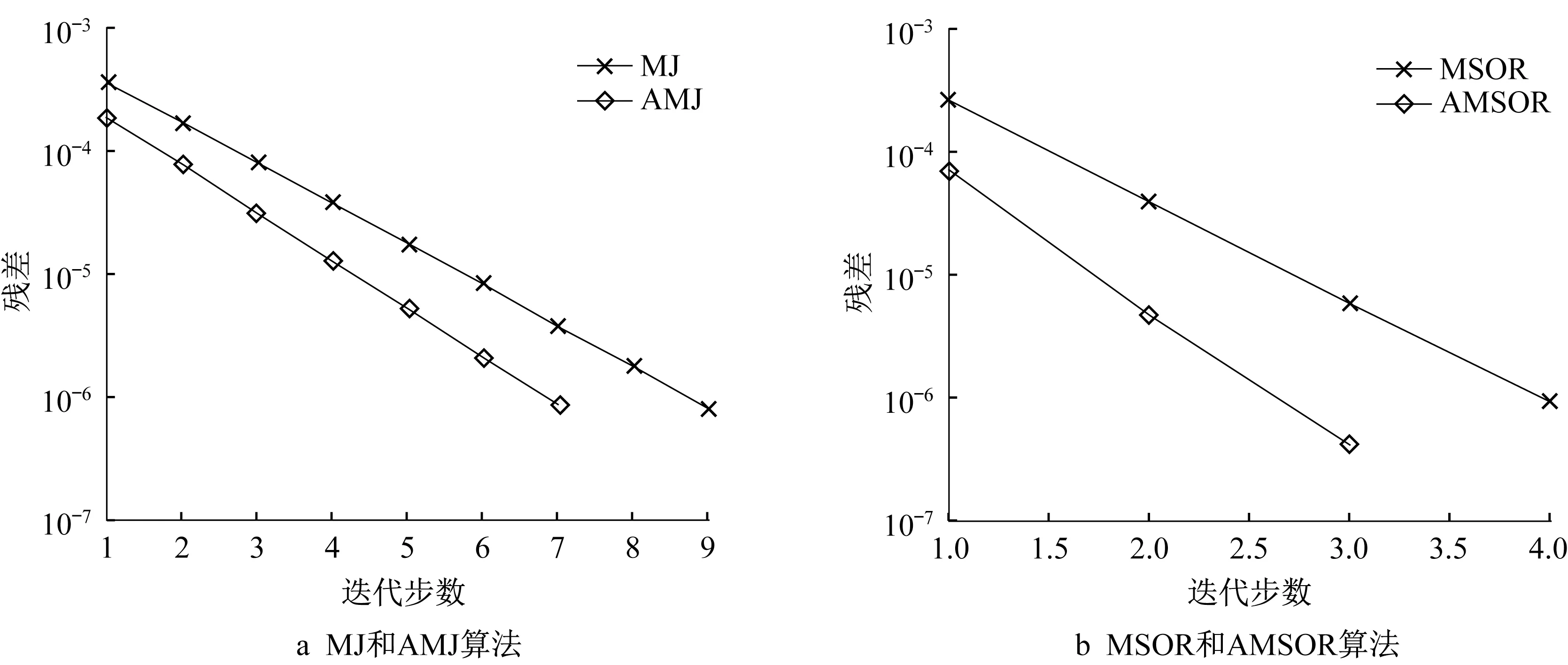
图1 例1两种算法的残差随迭代步数变化的比较Fig. 1 Residual comparison of two algorithms for example 1
当μ= 4时系数矩阵变得更加对角占优。从表4可以看出,在相同的矩阵维数下,6 种方法的迭代步数与时间少于表3 中的结果,并且加速模系矩阵分裂迭代法仍优于相对应的模系矩阵分裂迭代法。
表5 列出了μ= 2 时,α以0. 2 为间隔从1. 0 到2. 2 变化以及矩阵维数增加时,MSOR 及AMSOR算法迭代步数与迭代时间的数值结果。
从表5 中可以看到,当μ= 2,矩阵维数为400、1 600、3 600 和6 400 时,MSOR 相对应的最优参数分别为1. 8、1. 8、1. 6和1. 6,而AMSOR的最优参数分别为1. 6、1. 6、1. 8和1. 8。
表6和表7中列出了当μ分别为2和4,矩阵维数增大时在最优参数下6 种方法的迭代步数、迭代时间以及残差范数的比较结果。

表5 例2中当α变化时MSOR和AMSOR的迭代步数与时间(μ=2)Tab. 5 IT and CPU for MSOR and AMSOR with the change in α for example 2(μ=2)

表7 例2中最优参数下6种方法的数值结果(μ=4)Tab. 7 Numerical results for six methods with optimal parameters for example 2(μ=4)

表6 例2中最优参数下6种方法的数值结果(μ=2)Tab. 6 Numerical results for six methods with optimal parameters for example 2(μ=2)
表6 和表7 中的数值结果进一步验证了从表3和表4得到的结论,并且6种方法对于对称矩阵的迭代步数与时间略多于非对称矩阵。测试的6种算法中AMSOR 算法的计算效率优于其他5 种方法,并且所有的加速模系矩阵分裂迭代法仍优于相对应的模系矩阵分裂迭代法。
5 结论
本文构造了求解一类隐式互补问题的加速模系矩阵分裂迭代法。理论分析建立了系数矩阵为H+‐矩阵时的收敛性。数值结果表明,加速模系矩阵分裂迭代法在迭代步数和迭代时间上均优于传统的模系矩阵分裂迭代法。
然而对于隐式互补问题的求解,无论是模系矩阵分裂迭代法还是加速的模系矩阵分裂迭代法,内迭代的收敛速度在整个迭代过程中都有着十分重要的影响。合适的内迭代停止准则或迭代步数可以加速求解隐式互补问题的计算效率。目前,对于内迭代最优的停止准则以及停止的迭代步数还没有很好的结论,并且内迭代与外迭代之间如何平衡也是一个十分有挑战性的课题,这需要笔者进一步的研究。
