应用图像分析法构建食用亮蓝浓度与色度的定量关系
2020-12-04黄思涵万军伟
黄思涵,万军伟
(中国地质大学(武汉)环境学院,湖北 武汉 430074)
随着人类活动的不断加强,越来越多的污染物进入到地下水,并随地下水运动和扩散,而污染物在地下含水介质中的迁移规律十分复杂。室内砂槽模型的地下水溶质运移实验是研究地下水溶质迁移十分常见的方法,它能够通过控制介质、控制边界条件等揭示典型地下水介质和不同流场条件下溶质迁移的基本规律,因此得以普遍应用。以往室内地下水溶质运移砂槽模型实验多选择易溶盐(如NaCl)作为示踪剂,采用直接从砂槽中取样测试或预先埋置电导电极等方法来确定示踪剂浓度在空间和时间上的变化,但是由于室内砂槽模型的几何尺寸要比实际小很多,采用直接取样会使得流场发生变化,而采用预先埋置电导电极等传感器,又会使含水介质的渗透性发生很大改变,导致模型失真。为此,现在逐渐采用间接的方法获得示踪剂浓度随时间和空间的变化规律,如利用图像检测法通过记录实验全过程的图像信息[1],再利用这些图像信息分析示踪剂运移过程中图像数据和浓度的特征。在砂槽模型实验中,有色示踪剂经常被用来指示溶质的运移状况[2],而有色示踪剂的浓度与其颜色之间又存在着单调的变化关系,图像分析法正是利用示踪剂的这一特点,选取合适的示踪剂色彩模式,建立示踪剂浓度与色彩之间的函数关系式,从而在实验中通过图像分析法就能够间接计算出砂槽各处溶质的浓度,通过不同时间图像的对比又可以研究溶质浓度随时间的变化规律。
目前,罗丹明、荧光素钠等有色示踪剂已广泛地应用于地下水渗流示踪试验研究[3],但是实验发现这些示踪剂易被介质吸附、见光又易分解,较难建立示踪剂浓度与色彩空间准确的定量关系,而食用亮蓝是一种常用的食品添加剂,它具有无毒、水溶性强、不易被砂土颗粒吸附等特性,比荧光类示踪剂性能更加优越,但目前尚未建立孔隙介质中食用亮蓝浓度与色彩空间的定量关系。本文尝试采用图像分析法开展食用亮蓝浓度与色度的定量关系研究,并建立其数学模型,为地下水溶质运移示踪试验提供新的技术方法。
1 图像分析法
1.1 基于朗伯-比尔定律的基本理论
朗伯-比尔定律是图像分析法的物理基础[4],其定义是当一束平行单色光垂直通过某一均匀非散射的吸光物质时,其吸光度A与吸光物质的浓度C和吸收层厚度B成正比,而与透光度T成反比。根据这一原理,本次实验时采用固定砂槽模型的透光度和吸收层厚度,吸光度和物质浓度便成单调关系,颜色的深浅即反映物质的浓度。
图像分析法是利用图像传感器采集实验中已知浓度的有色溶液图像,之后利用计算机对色彩进行分析处理,得到有色溶液浓度与色度之间的定量关系,从而对后续的研究提供有力的支撑。本文利用食用亮蓝作为有色溶液进行图像分析。
1.2 图像分析法的研究历史
图像分析法已有数十年的研究历史,Schincariol等[5]在1993年就开始通过图像分析法确定示踪剂在砂箱中的浓度;Huang等[6]使用荧光示踪剂进行实验,在紫外灯源的照射下计算出了示踪剂的浓度分布状况;Persson[7]在RGB(红绿蓝)空间中使用了3种不同的土样进行示踪试验,并分别得到这三种土样中溶质浓度与图像颜色之间的关系;王康等[8]利用多种染色示踪剂进行了多孔介质非均匀流动显色示踪试验及显色图像信息化研究;Goswami等[9]使用铺满玻璃珠的水箱进行该类示踪试验,并对实验过程中存在的各种误差进行了系统分析;Catania等[10]使用荧光示踪剂来进行示踪试验,得到了示踪剂浓度与图像亮度之间的非线性关系。近年来,随着数码和计算机图像处理技术的不断发展,图像分析法也具有了更好的应用前景[11]。
2 色彩空间的原理与选择
2.1 色彩空间的原理
色彩空间又叫色域,是一种用来定量描述颜色的抽象数学模型[12]。色彩既是客观存在的(不同频率的光),又是主观感知的,有认识差异。色彩学中,人们建立了多种色彩模型,以一维、二维、三维甚至四维空间坐标来表示某一色彩,这种坐标系统所能定义的色彩范围即色彩空间。
在本次研究中需要建立示踪剂的浓度与该示踪剂在色彩空间中的某一数值之间的定量关系,即两者之间的数学模型。常用的色彩空间包括RGB和HSB等。例如在RGB色彩空间中,色彩被分解为三原色,即红(Red)、绿(Green)、蓝(Blue),且都被分成0~255一共256个等级,经过排列组合可以形成1 600多万种色彩。与RGB类似,常用的表示色彩的空间有HSB、CMYK等[13]。
2.2 色彩空间的选择
本次地下水溶质运移示踪试验初期先是利用RGB色彩空间进行试验,但是发现所用示踪剂食用亮蓝与RGB色彩空间三个颜色分量的任何一个参数值都不能建立良好的线性关系。之后对食用亮蓝的HSB色彩空间进行了研究,HSB包含色度(Hue)、饱和度(Saturation)和亮度(Brightness)三个部分,同样每一部分对应一个整数值。通过实验发现:饱和度(S)几乎不随示踪剂浓度发生变化,亮度(B)的变化范围很小,而色度(H)的变化范围较大,并且与示踪剂浓度之间呈现很好的相关性。因此,本实验最终选择 HSB 色彩空间中的色度(H)来进行数据拟合。
3 实验装置与设计
3.1 示踪剂的选择
本次地下水溶质运移示踪试验,最初采用的是传统的红色罗丹明示踪剂进行试验[14],虽然红色罗丹明具有良好的显色性,但是其附着性强,难以清洗,经过罗丹明溶液染色的砂槽模型中白色石英砂难以重新清洗恢复至白色,且被染色的砂箱同样无法恢复至原样,对于需要反复进行多次的室内模拟实验,无论是经济方面还是数据结果方面都会造成极大的不便。
通过查阅示踪剂相关文献[15],发现呈蓝色的食用亮蓝示踪剂非常契合本次实验,食用亮蓝是一种蓝色食品添加剂(双[4-(N-乙基-N-3-磺酸苯甲基) 氨基苯基]-2-磺酸甲苯基二钠盐),分子量为792.86,其在具有良好显色性的同时清理起来也相当方便,可以极大程度地减少示踪剂对于砂槽模型中石英砂的污染以及对不同次图像色度的干扰,且在实验中发现,加入的食用亮蓝颗粒易溶于水,一般情况下无颗粒状沉淀,并在长时间静置中观察到其色度并无改变。因此,最终选用食用亮蓝作为本次实验的示踪剂。
3.2 实验装置
本次地下水溶质运移示踪试验采用白色石英砂作为介质,且为了便于观测不能含有任何有色杂质,先用0.25 mm和0.35 mm的筛子对0.1~0.5 mm的石英砂进行筛分,得到粒径在0.25~0.35 mm比较均匀的石英砂,然后用稀盐酸进行浸泡去除石英砂表面附着的有色杂质,最后利用该粒径范围的石英砂,控制相同的密度,装填砂槽模型为后续地下水溶质运移示踪试验做准备[16]。
在砂槽模型开始之前,为了建立食用亮蓝的浓度与色度关系,首先开展了比色试验。比色试验是先在40个相同形状和体积的比色皿(长×宽×高为1 cm×1 cm×4.5 cm)中按相同密度装填上述与砂槽模型粒径相同的石英砂,同时配置好40种不同浓度的食用亮蓝溶液;然后将40种不同浓度的食用亮蓝溶液分别注入到之前准备好的40个装有石英砂的比色皿中,制备完成40个不同浓度和色度的食用亮蓝溶液石英砂比色皿;最后在DP6030长型补光灯照射的情况下用数码相机拍摄记录下这40个不同浓度食用亮蓝溶液比色皿的色彩图像,以备后面开展图像的数字化处理工作。
3.3 实验步骤
具体实验步骤如下:
(1) 用电子天平称取40份相同质量、相同粒径的石英砂(0.25~0.35 mm),分别装填到40个相同形状和体积的比色皿容器中,控制不同比色皿中石英砂的密度基本相同。
(2) 用电子天平称取40份不同质量的食用亮蓝粉末,将其分别装入1 L体积的容量瓶中,注满自来水(为了与后续砂槽模型实验用水一致),配置得到40种不同浓度的食用亮蓝溶液。经实验发现,当食用亮蓝溶液浓度达到3 g/L时,在溶液底部会开始出现少量沉淀,因此本次实验的食用亮蓝溶液浓度选取范围为0.01~3.00 g/L。然后将这40个已知浓度的食用亮蓝溶液分别注入到40个装有石英砂的比色皿中,得到40个食用亮蓝溶液浓度由高到低的含石英砂的比色皿。
(3) 将上述40个比色皿依次排好,在夜间排除其他所有光源的情况下,用DP6030长型补光灯照射,并用数码相机对40个比色皿进行了拍摄,得到40个不同食用亮蓝溶液浓度比色皿的彩色照片,见图1。

图1 不同浓度食用亮蓝比色皿的彩色图像Fig.1 Color images of cuvettes with different concentrations of edible brilliant blue
(4) 将拍摄记录的图像利用Matlab软件进行分析处理,提取得到40个不同颜色比色皿的色度(Hue)值(H),见表1。
3.4 实验结果与分析
由于本次实验与光学有非常紧密的联系,因此对于实验精度的要求很高。在实验中造成误差的原因有很多,如光线强度的变化、在配置溶液过程中电子天平的误差、石英砂在比色皿中随机排列方式造成的不同孔隙度等。如图1所示为实验所得到的不同浓度食用亮蓝比色皿彩色图像信息,40个比色皿按照食用亮蓝浓度从高到低的顺序从左向右排列,但是第13个和第38个比色皿的色度出现明显突变,如果忽视掉这种误差继续处理势必会对最终求得的结果产生影响。
为了提高实验的精度,降低系统误差带来的影响,本次实验数据一共由4组实验组成,每一组实验包含40个不同浓度的比色皿,按照其色度分布特征进行3组食用亮蓝浓度为0~1 g/L的实验和1组食用亮蓝浓度为1~3 g/L的实验,将获得的一共160组食用亮蓝数据取平均值之后进行整合,共求得57组食用亮蓝浓度与色度的对应关系,其具体实验数据见表1。
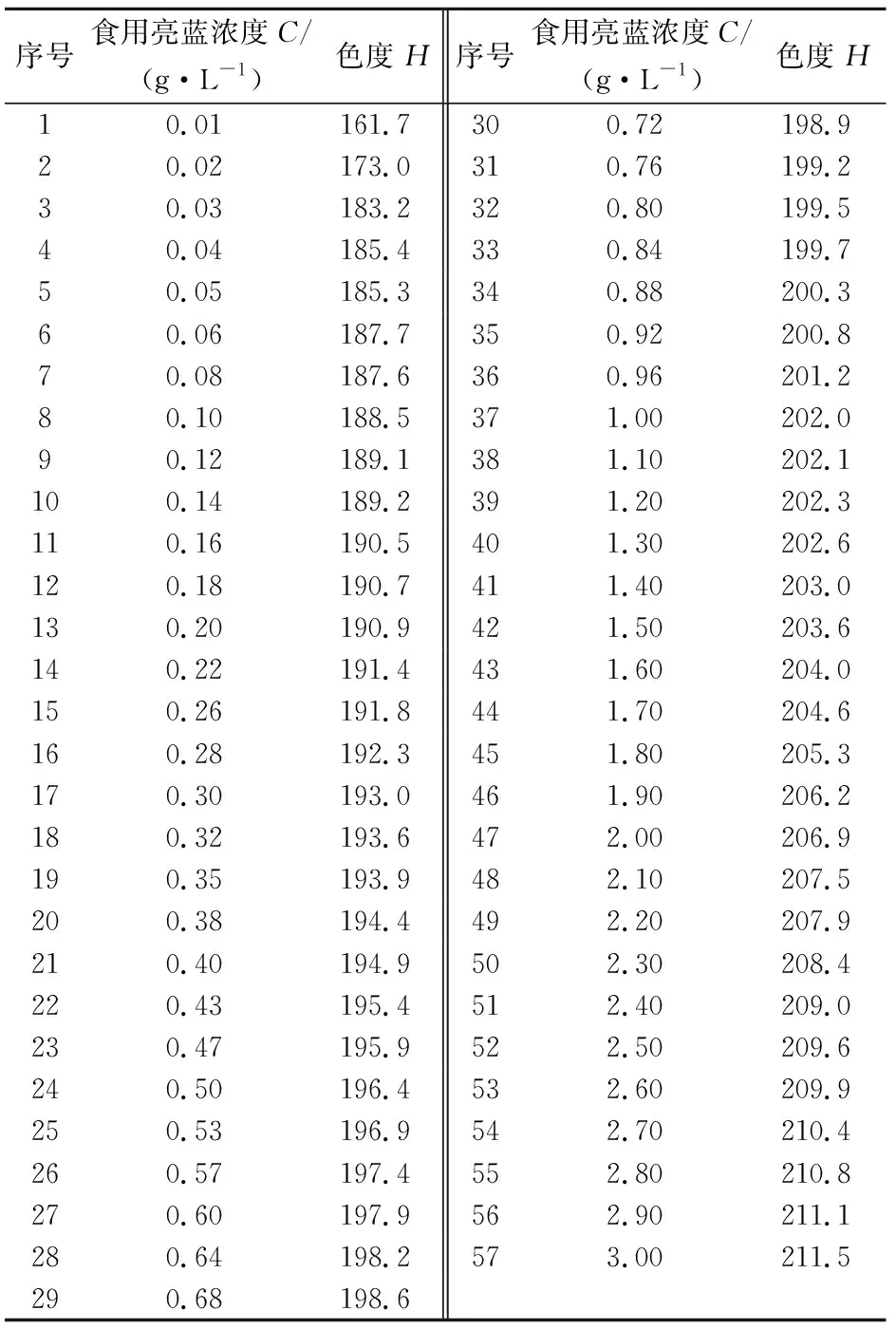
表1 食用亮蓝浓度和色度的实验数据Table 1 Experimental data of chromaticity and concen-tration of eligible brilliant blue
对表1中的实验数据进行拟合,可以得到食用亮蓝浓度C与色度H的数值关系图,见图2。
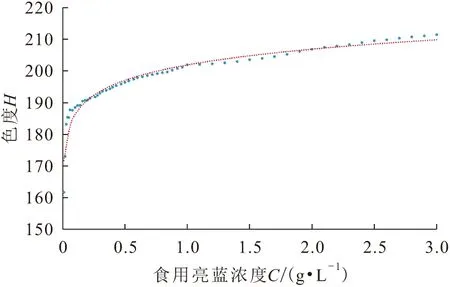
图2 食用亮蓝浓度与色度的数值关系(虚线为对数 拟合曲线)图Fig.2 Numerical relationship between chromaticity and concentration of edible brilliant blue(the solid line is a logarithmic fitting curve)
由图2可见,不同浓度食用亮蓝图像的HSB色彩空间的色度(H)与食用亮蓝的浓度(C)存在明显的相关性,且为单调增函数。
为了采用相关性最好的数学模型来描述两者之间的定量关系,将上述57组实验数据分别采用对数、指数、多项式、幂函数和线性方程进行了拟合,通过计算分别得到了5种数学模型的公式及其相关系数(R2值),见表2。

表2 食用亮蓝浓度C与色度H不同数学模型的拟合 公式及其相关系数(R2值)Table 2 Fitting formulas and R2 values of differentmathematical models for the concentration Cand chromaticity H of eligible brilliant blue
由表2可知,在5种数学模型中,对数函数模型的R2值最大,拟合效果最好,其函数关系表达式为
H=6.766 7lnC+202
(1)
式中:C为食用亮蓝的浓度(g/L);H为食用亮蓝在HSB色彩空间的色度值。
但是,通过观察表1中的实验数据可以发现:当食用亮蓝浓度C≤0.03 g/L时色度的变化很大;当亮蓝浓度C>0.03 g/L时色度的变化很小。因此,为了进一步提高数学模型的拟合精度,本研究将实验数据分为两组:第一组为食用亮蓝浓度C≤0.03 g/L的低浓度实验数据;第二组为食用亮蓝浓度C>0.03 g/L的高浓度实验数据,对这两组实验数据分别再采用不同的函数模型进行拟合。
图3为低浓度(C≤0.03 g/L)食用亮蓝浓度与色度的幂函数拟合曲线图,其中增加了纯净水的对照实验,并得到其色度值为60。
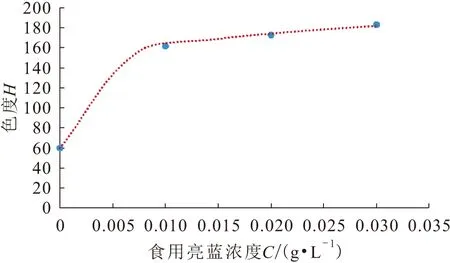
图3 低浓度(C≤0.03 g/L)食用亮蓝浓度与色度的 幂函数拟合曲线图Fig.3 Power function fitting curve of chromaticity and concentration of edible brilliant blue of low concentration (C≤0.03 g/L)
当食用亮蓝为低浓度(C≤0.03 g/L)时,分别采用对数、指数、多项式、幂函数和线性方程5种数学模型对食用亮蓝浓度与色度的关系进行了拟合,拟合得到的数学模型及其相关系数(R2值),见表3。

表3 食用亮蓝为低浓度(C≤0.03 g/L)时不同数学模 型的拟合公式及其相关系数(R2值)Table 3 Fitting formulas and R2 values of differentmathematical models for low concentration(C≤0.03 g/L) of edible brilliant blue
而当食用亮蓝为高浓度(C>0.03 g/L)时,食用亮蓝浓度与色度的幂函数拟合曲线图,见图4。
图4 高浓度(C>0.03 g/L)食用亮蓝浓度与色度的 幂函数拟合曲线图Fig.4 Power function fitting curve of chromaticity and concentration of edible brilliant blue of high concentration (C>0.03 g/L)
同样,当食用亮蓝为高浓度(C>0.03 g/L)时,分别采用对数、指数、多项式、幂函数和线性方程5种数学模型对食用亮蓝浓度与色度的关系进行了拟合,拟合得到的数学模型及其相关系数(R2值),见表4。

表4 食用亮蓝为高浓度(C>0.03 g/L)时不同数学模型的 拟合公式及其相关系数(R2值)Table 4 Fitting formulas and R2 values of differentmathematical models for edible brilliant blueof high concentrations (C>0.03 g/L)
对比表3和表4可知,在食用亮蓝浓度大于0且小于或等于0.03 g/L时幂函数模型的R2值最大(R2值为0.999 4),表明该数学模型的拟合效果最好;在食用亮蓝浓度大于0.03 g/L且小于或等于3 g/L时,也是幂函数模型的R2值最大,表明该数学模型的拟合效果最好;同时,观察到对数函数模型的相关系数也较大,表明拟合效果较好,但是根据色度的定义可以发现其数值恒大于0,与幂函数的性质吻合,不符合对数函数的定义。因此,最终采用幂函数的数学模型来模拟两者的定量关系,其具体表达式为
当0 g/L 当3 g/L≥C>0.03 g/L时,H=201.81C0.031 3. 本文通过室内砂槽模型实验运用图像分析法研究了食用亮蓝浓度与色度的定量关系,得到如下结论: (1) 食用亮蓝的浓度与色度之间存在很好的相关性,两者之间满足单调增函数关系。 (2) 用食用亮蓝HSB色彩空间的色度H值来描述食用亮蓝浓度与色度的关系,比其色彩空间的中的饱和度S和亮度B值以及其他色彩空间的数值关系分辨率更高。 (3) 食用亮蓝浓度C与色度H的整体关系更符合对数函数模型的变化规律,总体满足:H=14.937lnC+232.62,但该函数对低浓度食用亮蓝的刻画精度较低。 (4) 为了更高精度刻画低浓度食用亮蓝的浓度C与色度H的关系,可以采用分段幂指数函数的形式来描述:即当食用亮蓝浓度≤0.03g/L时,H=299.61C0.138 1;当食用亮蓝浓度>0.03 g/L时,H=201.81C0.031 3。 本次室内砂槽模型实验通过图像分析法对食用亮蓝浓度与色度的定量关系展开了研究,并求得了拟合效果最好的数学模型,为运用图像分析法解决溶质运移的问题提供了新的思路。但是受到时间、实验条件等因素的限制,研究还不够全面,在图像分析法的运用方面还有很大的研究空间,因此在本文的研究基础上提出以下几点期望: (1) 本文的目的为提供一种图像信息处理的思路和经过对比分析得到适用于室内地下水溶质运移砂槽模型实验的示踪剂。最终所求得的数学模型的实质是示踪剂浓度与色度的关系曲线,而图像的色度值对光照的影响十分敏感,食用亮蓝的色度值随着光源强度的增加而增加、随着光源强度的减少而减少,因此该数学模型不能普遍适用于任何情况下食用亮蓝浓度与色度之间的关系研究,在其他环境中进行图像分析时需要对光源强度进行统一。 (2) 不同的示踪剂之间有不同的性质,其特性也决定于其适用的领域。除了本次室内地下水溶质运移砂槽模型实验所采用的食用亮蓝以外,还有荧光素钠、罗丹明等更适合于野外实地实验的示踪剂,而对于这些示踪剂,还需要重新探索其浓度与哪个色彩空间中的色度相关性较好,并进一步探究其对应关系的表达式。4 结论与展望
