基于组合赋权-后悔理论的城市综合管廊运维总体风险评估

涂圣文，赵振华，邓梦雪，王 冰

(贵州师范大学材料与建筑工程学院，贵州 贵阳 550025)

综合管廊也称为管线共同沟，是修建在城市道路地下的隧道式构造物，用于放置两类及以上城市工程管线的构筑物，一般还设置有投料口、进风排风井、人员出入口、通风、监控等附属设施[1]。城市地下综合管廊将给排水、通讯、电力、燃气以及热力等各类市政管线统筹放置在地下公用空间内，减少了各类管线的分开外置，美化了城市景观，减少了管线维修时反复开挖道路的施工作业，降低了管线维修的综合成本，是城市现代化的标志之一，也是现代城市建设的趋势[2]。与发达国家和地区相比，我国地下城市综合管廊建设起步较晚，经过几十年的酝酿，进入2014 年之后，随着综合管廊政策密集出台并不断加码、细化，才进入了井喷式的发展阶段，并在“十三五”期间迎来了建设高潮[3-4]。相较于传统直埋式和架空铺设式的模式，将市政管线集中设置在地下综合管廊内，除了具有集约化利用资源的优势外，还可抵御地震、台风、冰冻、侵蚀等自然灾害。但由于各类高危管线的集中入廊，各种管线集中放置在同一空间内，在内、外部因素联合作用和管线间相互影响下，也容易发生电缆破损、管道泄漏导致中毒、爆炸、火灾等灾害的风险[5-6]。

随着我国城市综合管廊建设高潮期而来的，是今后若干年大量综合管廊运维关键时期的到来，如何保障综合管廊的安全，防控综合管廊的各类运维灾害，维护城市重要“生命线”的运营安全，是一个迫切需要关注的严峻问题。近年来，许多研究人员针对城市综合管廊的运维灾害防控问题开展了大量的研究工作。如郭佳奇等[5]系统划分了城市地下综合管廊运维期的灾害类型，分析了城市地下综合管廊火灾和震害的产生机理，并提出了城市地下综合管廊运维期灾害防控的基本原则与应对措施；王述红等[6]建立了综合管廊单一灾种的危险评价指标，应用模糊数学方法和耦合度模型研究了多灾种之间的耦合关系，并提出了综合管廊多灾耦合致灾的风险评价方法；李芊等[7]运用DEMATEL 方法对综合管廊运维管理过程中的风险因素进行了影响程度和重要程度排序，识别了运维管理过程中的关键风险因素，并对关键风险因素提出了具体的防范措施；邓小娇等[8]和王玉琪等[9]采用FLUENT 软件，吴建松等[10]采用OpenFOAM软件，针对城市综合管廊正常通风—泄漏报警—事故通风—警报解除的全过程进行了动态分析，研究了输气管道在城市综合管廊舱室泄漏扩散的基本规律，为燃气泄漏事故应急决策与应急救援提供了理论指导；王明年等[11]采用三维火灾动力学模拟软件FDS5.0，针对电缆火灾对城市综合管廊舱室内部火灾发展过程及温度分布进行了模拟研究，并利用ANSYS有限元软件对城市综合管廊舱室结构进行了热分析，得到火灾下城市综合管廊结构温度场分布以及结构高温损伤深度数据；黄萍等[12]建立了综合管廊火灾安全评价指标体系，提出利用基于AHP-证据理论的评价模型对综合管廊火灾安全等级进行评价。

总体来看，现有研究较多关注的是城市综合管廊燃气泄漏、火灾等这些专项型灾害的影响及其防控，对城市综合管廊运营维护阶段的总体风险评估研究还相对较少。为了有效评估城市综合管廊设施在运维期间的总体风险状态，为合理制定城市综合管廊设施的风险防控措施和应急响应措施提供依据，本文在构建城市综合管廊运维总体风险评估指标体系的基础上，运用基于博弈论思想的组合赋权技术确定了各项评估指标的权重系数，并引入后悔理论来对城市综合管廊运维总体风险进行评估，以为类似的基础设施风险评估提供新的思路和技术手段。

1 城市综合管廊运维总体风险评估指标体系建立以及指标权重确定

1.1 评估指标体系建立

城市综合管廊的运维管理在我国还属于起步阶段，目前相关部门还尚未出台城市综合管廊运维风险评估的相关规定。为了确定城市综合管廊运维总体风险评估的指标体系，除了参考现有的文献[5-7,12-13]等相关研究成果之外，本研究还走访调研了贵安新区、六盘水、长沙等地的综合管廊运维公司。

按经典风险管理理论中风险源辨识的思路，从“人、机、环、管”四个角度建立综合管廊风险评估指标[12]。“人”的角度，主要指的是综合管廊运维工作人员的专业化程度、风险防范意识和工作状态等；“机”的角度，主要指的是运维阶段综合管廊廊体、管线、附属设施、运维设备设施等各类设施是否存在不能正常工作以及发生各种灾害的风险；“环”的角度，主要指的是综合管廊运维中外部地质、水文、气象环境和内部空气、通风、湿度等因素可能导致的风险；“管”的角度，主要指的是综合管廊运维管理方面，诸如管理机构是否健全、管理制度是否完善、管理档案是否完整规范、应急预案是否切实可行等。

将上述“人、机、环、管”四个方面的评估指标进行细化、归纳，建立城市综合管廊运维总体风险评估指标体系，见表1。为了便于从量化的角度分析表1中各项评估指标的风险程度，参考文献[6]、[12]和[14]等关于风险评价、风险评价等级划分和量化取值标准，将表1中各项评估指标的风险状态划分为5个风险等级，各风险等级对应的量化评分值见表2。

表1 城市综合管廊运维总体风险评估指标体系Table 1 Index system of overall risk assessment for urbanutility tunnel during operation and maintenance

表2 城市综合管廊运维风险等级划分及其评分值[6,12,14]Table 2 Risk grade classification and scoring valueof urban utility tunnel during operation andmaintenance

1.2 指标权重确定的博弈论组合赋权法

一般来说，指标权重确定的方法主要分为主观赋权法和客观赋权法。主观赋权法主要依赖专家的经验，赋权结果受专家主观意志的影响明显；客观赋权法则完全依据指标原始评分数据包含的信息量，通过数学模型的计算分析来确定指标的权重,虽然具有较强的数学理论依据，但却完全忽略了专家积极的主观能动性。因此，近年来在安全评价、风险评估领域更多倾向于采用主、客观组合赋权法来确定指标的权重[15-17]。本文采用基于博弈论思想的主、客观组合赋权法来确定城市综合管廊运维风险评估指标的权重，其中主观赋权法选用G1法，客观赋权法运用熵权法。

1.2.1 G1法确定指标的主观权重

主观赋权的G1法最先由郭亚军[18]于2002年提出，该方法能克服层次分析法存在的计算量大、计算过程繁琐、需要一致性检验等缺点，且特别适合于像城市综合管廊运维风险评估这样因素多、规模大的问题，其实现步骤如下[18-19]：

(1) 由专家按指标之间的相对重要性对指标进行排序，并给定相邻两指标xj-1、xj(j=2,3,…,n，其中n为指标数量)之间的重要性程度之比rj。

(2) 由下式计算第n个指标的主观权重wn:

(1)

(3) 由下式计算其他n-1个指标的主观权重：

wj-1=rjwj(j=n,n-1,…,3,2)

(2)

1.2.2 熵权法确定指标的客观权重

属于客观赋权法的熵权法其基本原理是通过充分挖掘指标原始评分值中包含的信息量，根据各指标的变异程度，利用信息熵计算各指标的熵权，再通过熵权计算出各指标的权重系数，其计算过程如下[20]：

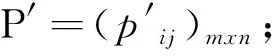
(2) 由信息熵的概念，计算第j个指标的熵值ej：

(3)

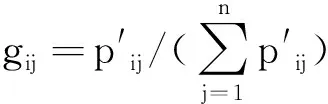
(4)

(3) 计算第j个指标的客观权重wj:

(5)

1.2.3 基于博弈论确定指标的组合权重

在由G1法确定指标主观权重和熵权法确定指标客观权重后，引入博弈论的思想来确定评估指标的组合权重。根据博弈论的思想，若将G1法确定的指标主观权重W1=(w11,w12,…,w1n)和熵权法确定的指标客观权重W2=(w21,w22,…,w2n)看作是博弈的双方，最优组合权重可以看作是博弈双方达成平衡状态。从数学角度来看，平衡状态下，应满足W1和W2与指标组合权重之间的离差之和最小，其实现步骤如下[21]：

(1) 记由W1和W2的线性组合表达的指标组合权重向量W为

=λ1W1+λ2W2

(6)

式中:λ1、λ2为线性组合系数。

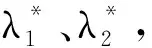
min(‖W-W1‖2+‖W-W2‖2=min(‖λ1W1+λ2W2-W1‖2+‖λ1W1+λ2W2-W2‖2)

(7)

s.t.λ1+λ2=1,λ1,λ2≥0

(8)

(3) 根据微分原理，模型(7)取得最小值的一阶导数条件为

(9)

(4) 将公式(8)求得的线性组合系数λ1、λ2进行归一化处理，有：

(10)

进而得到评估指标的最优组合权重为

(11)

2 基于后悔理论的城市综合管廊运维总体风险评估

城市综合管廊运维总体风险评估属于多属性决策问题的范畴，一般需要依赖于决策理论予以解决。现代决策理论发展迅速，决策方法众多，总体上来看，考虑决策者行为的决策方法已得到了广泛应用[22]。目前，考虑决策者行为的决策方法主要分为两类：一类假设决策者行为是完全理性的，其主要代表是期望效用理论；另一类则假设决策者行为是有限理性的，其主要代表是前景理论和后悔理论。由于有限理性比较接近人的决策行为实际情况，因此有限理性的决策方法已逐渐成为决策理论研究的热点之一。其中的后悔理论模型运算简单，不需要较多的参数，能切实反映决策者的决策行为，而且后悔理论应用于安全和风险评估领域，能够有效规避风险，减少不必要的损失[22-23]。故本文采用后悔理论来对城市综合管廊运维总体风险进行评估。

2.1 后悔理论概述

后悔理论的主要思路是假设决策者的决策过程是一个综合比较的过程，即在决策过程中，决策者会有意识地将自己选择的方案与其他备选方案进行比较，若决策者选择的方案次于其他方案，决策者会感到后悔；反之，若决策者选择的方案优于其他方案，决策者就会感到欣喜。因此，决策者的决策过程具有以下两个方面的特征：①最终的选择方案取决于对决策产生的后悔值和欣喜值的预期平衡；②决策者选择过程中会尽量避开会产生后悔的方案。从这个意义上来看，后悔理论从本质上就具备规避风险的优势。

后悔理论主要通过感知效用函数来体现，其由度量选择方案的效用函数和后悔-欣喜函数两部分所构成，其一般形式可表示如下：

D(x,y)=h(x)+R(h(x)-h(y))

(12)

式中：x,y分别为两个备选方案;D(x,y)为选择方案x的感知效用函数;h(x)和h(y)分别为选择方案x和方案y的效用值;R(h(x)-h(y))为后悔-欣喜值，R>0表明决策者对在方案x、y中选择方案x感到喜悦，反之R<0则表明决策者对在方案x、y中选择方案x感到后悔。

上述过程也可以扩展到多方案的选择，若存在l个备选方案供决策者选择，根据感知效用函数公式(12)，决策者选择方案xi(i=1,2,…,l)的感知效用函数可表示为

Dxi=h(xi)+R(h(x*)-h(xi))

(13)

其中，h(x*)=min{h(xi)∣i=1,2,…,l}。易知，h(x*)-h(xi)≤0，R(h(x*)-h(xi))≤0表示后悔值。

2.2 后悔理论评估步骤

后悔理论用于城市综合管廊运维总体风险评估的主要实现步骤如下：

步骤1:构建各指标的原始评分矩阵。对表1中城市综合管廊运维总体风险评估指标体系各准则层的指标，按表2中的风险等级评分值进行评分，建立各评估指标的原始评分矩阵:Q=(qji)nxm(i=1,2,…,m;j=1,2,…,n。其中m为参与评估的专家人数，n为指标数量)。显然，有Q=PT。

步骤2:构建理想方案。根据原始评分矩阵Q，构建理想方案B=[b1,b2,…,bn]，其中bj(j=1,2,…,n)为第j个评估指标的理想值，本文中由表2可知风险等级越高评分值越小，因此每个评估指标的理想值取各专家评分的最小值，以减少后悔程度。

步骤3:构建评分值的效用值矩阵。计算各评分值的效用值，需要先选择合适的效用函数。如前文所述，决策过程中决策者会尽量避开会产生后悔的方案，即有着尽量回避风险的选择特性。因此，最适宜的效用函数h(x)应该是单调递增的凹函数，即满足h′(x)>0，h″(x)<0。实际的安全风险评估应用中，一般选择幂函数来作为效用函数[14,22]，有：

h(qji)=(qji)α

(14)

式中:α为函数的参数，一般0<α<1，本文中参照文献[14]、[22]，α取值为0.9。

于是，评分值的效用值矩阵H可表示为

H=((qji)α)n×m

(i=1,2,…,m;j=1,2,…,n)。

步骤4:构建评分值的后悔-欣喜值矩阵。基于决策者回避风险的选择特性，与效用函数的性质一样，后悔-欣喜函数R(·)也应该是单调递增的凹函数，一般情况下，后悔-欣喜函数R(·)采用如下的形式[23]：

(15)

式中:β为函数的参数，也称作后悔规避系数，一般β>0，本文中参照文献[14]、[22]，β取值为0.013 3。

于是，评分值的后悔-欣喜值矩阵R可表示为

(i=1,2,…,m;j=1,2,…,n)。

步骤5:构建感知效用值矩阵。由上文所述后悔理论的基本原理，感知效用值为效用值和后悔-欣喜值之和，即感知效用值矩阵D可表示为

步骤6:计算综合评估结果。运用上文第1.2节所述博弈论组合赋权法求得第k个准则层下第j个指标的组合权重wkj(k=1,2,…,4;j=1,2,…,n)，根据下式对各准则层进行加权求和，有：

(16)

式中:Sk为第k个准则层的综合评估值；其他参数同前述。

最后，目标层总的风险评估结果由下式求得：

(17)

式中:S为总的风险评估值;wk为第k个准则层的权重。

3 实例应用与分析

本文以西南某国家级新区试点项目城市综合管廊运维总体风险评估为例，阐述本文方法的应用步骤与效果。

该项目研究过程中，共邀请到5位本领域的专家，通过向专家提供该城市综合管廊项目相关的运维管理资料，并结合邀请各位专家到该综合管廊项目运维管理公司进行走访调研的方式，最后请各位专家按照表2的风险等级划分及其评分值，分别对表1的各分项评估指标进行打分，专家评分结果汇总于表3。

表3 城市综合管廊运维总体风险评估专家评分值Table 3 Scoring value of experts of overall risk assessment for urban utility tunnel during operation and maintenance

3.1 指标权重计算

对该试点项目城市综合管廊运维总体风险进行评估时，首先需要根据前述基于博弈论的组合赋权法求得表1中各项评估指标的权重系数。

3.1.1 G1法确定指标的主观权重

以准则层4个一级指标即人的因素A、设施因素B、环境因素C和管理因素D的权重确定为例，通过专家评价确定这4项评估指标的重要度排序为：B>C>A>D，按重要度排序的各指标权重依次记为w1、w2、w3、w4。相邻指标之间重要性程度之比由专家参照文献[19]的打分标准分别给出，具体比值依次为：r2=w1/w2=1.5，r3=w2/w3=1.3，r4=w3/w4=1.2。根据公式(1)，可计算得到w4=0.164，进而可计算得到w3=0.196、w2=0.256、w1=0.384。则G1法确定的准则层4个一级指标的主观权重为(0.196,0.384,0.256,0.164)。

按同样的步骤，通过专家打分法确定“人的因素”准则层下3个二级指标的主观权重为(0.433,0.309,0.258)，“设施因素”准则层下8个二级指标的主观权重为(0.252,0.14,0.108,0.21,0.09,0.068,0.075,0.057)，“环境因素”准则层下4个二级指标的主观权重为(0.410,0.293,0.163,0.134)，“管理因素”准则层下4个二级指标的主观权重为(0.334,0.257,0.214,0.195)。

3.1.2 熵权法确定指标的客观权重

根据前文所述熵权法确定指标客观权重的计算步骤，按表3中各项指标评分值进行计算，可得到指标层19个指标的客观权重为(0.101,0.142,0.027,0.051,0.185,0.043,0.027,0.030,0.052,0.188,0.016,0.004,0.044,0.008,0.032,0.027,0.010,0.006,0.007)。于是，准则层4个一级指标的客观权重为(0.269,0.593,0.088,0.050)，将各准则层下二级指标的权重进行归一化处理，可得“人的因素”准则层下3个二级指标的客观权重为(0.376,0.526,0.098)，“设施因素”准则层下8个二级指标的客观权重为(0.085,0.314,0.072,0.045,0.051,0.088,0.317,0.028)，“环境因素”准则层下4个二级指标的客观权重为(0.042,0.498,0.095,0.365)，“管理因素”准则层下4个二级指标的客观权重为(0.536,0.211,0.116,0.137)。

3.1.3 博弈论确定指标的组合权重

按同样的步骤，可计算求得“人的因素”准则层下3个二级指标的组合权重为(0.376,0.534,0.090)，“设施因素”准则层下8个二级指标的组合权重为(0.145,0.252,0.084,0.104,0.065,0.081,0.231,0.038)，“环境因素”准则层下4个二级指标的组合权重为(0.175,0.424,0.120,0.281)，“管理因素”准则层下4个二级指标的组合权重为(0.478,0.224,0.144,0.154)。

3.2 城市综合管廊运维的总体风险评估与计算

按前文所述后悔理论的实现步骤，首先根据4个准则层各指标的原始评分矩阵，分别计算各准则层的效用值矩阵、后悔-欣喜值矩阵和感知效用值矩阵。以“人的因素”准则层为例，分述如下：

(1) 根据表3中风险评估专家指标评分值，构建“人的因素”准则层原始评分矩阵QA：

(2) 构建矩阵QA的理想方案BA：

BA=[5,3.5,7.3]T

(3) 根据公式(14)，可计算求得“人的因素”准则层各项指标评分的效用值矩阵HA：

(4) 根据公式(15)，可计算求得“人的因素”准则层各项指标评分的后悔-欣喜值矩阵RA：

(5) 将效用值矩阵HA和后悔-欣喜值矩阵RA相加，得到“人的因素”准则层感知效用值矩阵DA：

同样的步骤，可分别计算得到“设施因素”准则层感知效用值矩阵DB、“环境因素”准则层感知效用值矩阵DC、“管理因素”准则层感知效用值矩阵DD如下：

然后，依据公式(16)，可计算求得“人的因素”各项指标加权求和评估值S1为4.643，“设施因素”各项指标加权求和评估值S2为4.781，“环境因素”各项指标加权求和评估值S3为6.133，“管理因素”各项指标加权求和评估值S4为6.828；再依据公式(17)，可计算求得本试点项目总的风险评估值S为5.11，根据表2可知，该城市综合管廊项目运维总体风险水平为中度风险。

3.3 风险评估结果分析

由上述风险评估计算结果可以看出，由于引入了主客观组合赋权法，该综合管廊项目运维风险评估指标权重的确定更加符合实际情况。如单纯由客观熵权法确定的人的因素、设施因素、环境因素和管理因素4个一级指标的权重为(0.269,0.593,0.088,0.050)，虽然此客观权重基本能反映各项指标之间的重要度排序，但环境因素的权重明显偏小。通过引入G1法，通过专家根据自身合理经验判断确定各项指标的主观权重后，基于博弈论的思想，构建融合主、客观权重值的指标组合权重为(0.248,0.532,0.137,0.083)，一方面考虑了原始评分数据包含的信息量，另一方面也考虑了专家积极的主观能动性，使得指标权重结果更加符合实际情况，更具代表性。

为了检验后悔理论用于城市综合管廊运维总体风险评估的效果，该试点项目研究过程中，同时采用风险评估常用的模糊综合评价法、集对分析法对该综合管廊项目运维总体风险进行了评估，3种评估方法的风险评估结果汇总于表4。

表4 3种评估方法的风险评估结果Table 4 Comparison of risk assessment resultsby three assessment methods

由表4可知，后悔理论评估法与模糊综合评价法和集对分析法的风险评估结果均为中度风险，后悔理论评估法与常用的风险评估方法的评估结果一致，说明后悔理论评估法用于城市综合管廊运维总体风险评估是可行的；同时，后悔理论评估法的综合评估值为5.11，较模糊综合评价法的综合评估值5.85偏小，这表明后悔理论评估法得到的综合管廊运维风险更高，体现了后悔理论从本质上就具备规避风险的优势。由此可见，后悔理论应用于城市综合管廊运维总体风险评估领域，能够有效规避风险，减少不必要的损失。

此外，从上述后悔理论的评估计算过程可知，后悔理论不仅能获得城市综合管廊运维的总体风险状况，也能得到各准则层的风险状况，便于了解风险发生的源头，采取针对性强的风险应对措施。如上文计算求得准则层“人的因素”的风险评估值S1为4.643，“设施因素”的风险评估值S2为4.781，“环境因素”的风险评估值S3为6.133，“管理因素”的风险评估值S4为6.828，由风险等级划分标准可知，“人的因素”和“设施因素”为中度风险等级，“环境因素”和“管理因素”为低度风险等级。其中，“人的因素”的风险评估值最低，表明该准则层风险最高，这主要与工作人员的风险防范意识较低有关；“管理因素”的风险评估值最高，表明该准则层风险最低。通过对该综合管廊运维管理中心进行调研可知，该综合管廊的运维管理机构齐全、制度完善、资料完整，且具有切实可行的风险应急预案，因此要改善该综合管廊项目的总体风险状况，应该从提升管理人员的风险意识和专业化水平等方面予以考虑。

4 结论与建议

(1) 为充分发挥主观赋权法和客观赋权法各自的优势，本文在城市综合管廊运维风险评估中，采用基于博弈论思想的主、客观组合赋权法来确定风险评估指标的权重，其中主观赋权法选用G1法，客观赋权法运用熵权法。实例应用研究表明：融合了主、客观权重值的指标组合权重，一方面考虑了原始评分数据包含的信息量，另一方面也考虑了专家积极的主观能动性，使得指标权重结果更加符合实际情况，更具代表性。

(2) 本文提出了基于有限理性的后悔理论来对城市综合管廊运维总体风险进行评估，并将评估结果与模糊综合评价法、集对分析法两种常用的风险评估方法的评估结果进行了对比分析。实例研究结果表明：后悔理论评估法与常用的风险评估方法的评估结果基本一致，说明后悔理论用于城市综合管廊运维总体风险评估是可行的；同时，后悔理论不仅能确定风险等级，还能给出量化的风险评估值，这是因为后悔理论从本质上就具备规避风险的优势，其给出的量化的风险评估值较其他风险评估方法偏小，有利于减少不必要的损失；另外，后悔理论不仅能获得城市综合管廊运维的总体风险状况，也能得到各准则层的风险状况，便于了解风险发生的源头，采取针对性强的风险应对措施。

(3) 需要指出的是，城市综合管廊运维风险评估中，风险评估指标划分的标准是否合理、指标的评分取值是否合理也会对评估结果产生较大的影响。因此，在后续的研究工作中，还需要进一步补充和完善城市综合管廊运维风险评估指标体系，进一步研究指标评分的取值问题和安全等级划分标准问题，以进一步提高评估指标体系的科学性，增强评估结果的全面性和客观性。