激光强度对单阶谐波增强的影响

刘 航,刘 辉,冯立强,

(1. 辽宁工业大学化学与环境工程学院,锦州 121001; 2. 辽宁工业大学理学院,锦州 121001)

1 引 言

高次谐波是强激光场与原子、分子和固体相互作用时产生的一种非常重要的现象[1]. 在过去二十多年的时间里,高次谐波在分子轨道成像[2]; 化学反应追踪[3]; 探测超快电子运动[4]; 产生阿秒脉冲[5]及单阶谐波脉冲[6]等领域起到了关键作用.

当体系采用原子或分子时,高次谐波的产生可由半经典的三步模型[7]来理解. 首先,激光调制库仑势使电子隧穿电离; 随后,被电离的电子在激光驱动下加速并获得能量; 最后,在激光反向驱动下,电子有几率与原母核发生碰撞,进而辐射出光子能量为基频场倍数的高阶谐波. 一般来说,谐波光谱连续区的强度变化不是很明显,呈现谐波平台区. 因此,通过叠加平台区的谐波可以获得孤立阿秒脉冲[8-10].

除了利用高次谐波获得孤立的阿秒脉冲,另外一个非常重要的应用是获得单阶谐波脉冲. 这一应用对于获得自由电子激光器的种子光源非常有帮助. 基于三步模型,谐波辐射每半个光学周期发生一次,因此,谐波辐射的相位(或辐射时间)是不一致的. 这导致谐波辐射强度的下降. 基于此点,研究人员利用多色场激光波形调制来实现局部谐波相位的匹配,进而获得单阶谐波的增强[11-13]. 最近,Liu等[14-15]利用激光波形调控机制理论获得了一种W形状的波形. 在此波形下成功实现了单阶谐波的增强. 但是,其对单价谐波增强的强度范围并没有研究. 因此,本文理论研究了激光强度对单价谐波增强范围的影响. 结果表明,单阶谐波的增强现象不仅来源于谐波辐射的折叠区域,并且与多重谐波辐射能量峰的干涉有关. 这对Liu等[14-15]的研究结果做出了补充.

2 计算方法

He原子在激光场下的动力学行为可由薛定谔方程来描述,

(1)

其中,V(r)=-1.353/r为He原子的库仑势能. 组合驱动场可以描述为,

E(z,t)=E1f1(t)cos(ω1t+bt2)+

E2f2(t)cos(ω2t)

(2)

fi(t)=exp[-2ln(2)t2/τi2]

(3)

这里,Ei、ωi和τi(i= 1,2)分别表示双色组合场中各分量场的振幅、频率和脉宽.

高次谐波光谱可表示为：

(4)

其中,ω表示谐波频率,a(t)=-〈ψ(r,t)|[H(t),[H(t),z]]|ψ(r,t)〉为偶极加速度.

3 结果与讨论

图1(a)给出双色啁啾激光场驱动He原子辐射高次谐波图. 其中,基频场为15 fs-1600 nm,I1= 2.0×1014W/cm2,b= 6×10-5. 控制场为8.74 fs-800 nm,I2= 2.0×1014W/cm2. 由图1(a)可知,在该波形下,谐波辐射光谱呈现单价谐波的增强现象. 具体来说,第523次谐波与谐波平台区的强度相比被增强了7.5倍. 图1(b)和1(c)给出了上述激光包络图以及谐波辐射的时频分析图[16]. 根据文献[14-15]可知,在W波形下,谐波辐射的增强来源于谐波辐射能量峰的叠加结构. 对应于本文的激光波形可见[图1(b)所示],当电子在A点附近发生电离后,被电离的电子在激光驱动下进行加速,最后在激光反向时与母核在R点附近回碰,进而呈现出谐波辐射能量峰PA,如图1(b)和1(c)所示. 这里,由于激光波形在t=0～1.25 T (T 为1 600 nm激光的光学周期)呈现出反向波包,导致电子在这一特殊结构下会首先减速然后再加速,进而在谐波辐射能量峰PA上呈现了一个折叠区域[图1(c)所示]. 这一折叠区域的范围只覆盖523次谐波,因此,第523次谐波与谐波平台区的其他谐波相比,其强度得到了增强. 但是,仔细分析谐波辐射能量图可见,在PA峰附近还有一个强度较弱的能量峰PB. 分析激光波形可知,PB是由电子在B点处电离在R点处回碰产生的. 并且其能量也覆盖523次谐波范围. 因此,第523次谐波的强度应该是由PA和PB共同作用产生的. 但是,由于PA和PB谐波辐射时间不同,因此其谐波辐射相位不匹配会导致干涉减小的现象. 也就是说,第523次谐波的强度的增强不仅是由谐波能量峰的叠加结构产生的,而且还与不同谐波辐射能量峰的干涉有关. 为了进一步确定这一结论,本文对不同激光强度下单价谐波增强的比率做了研究.

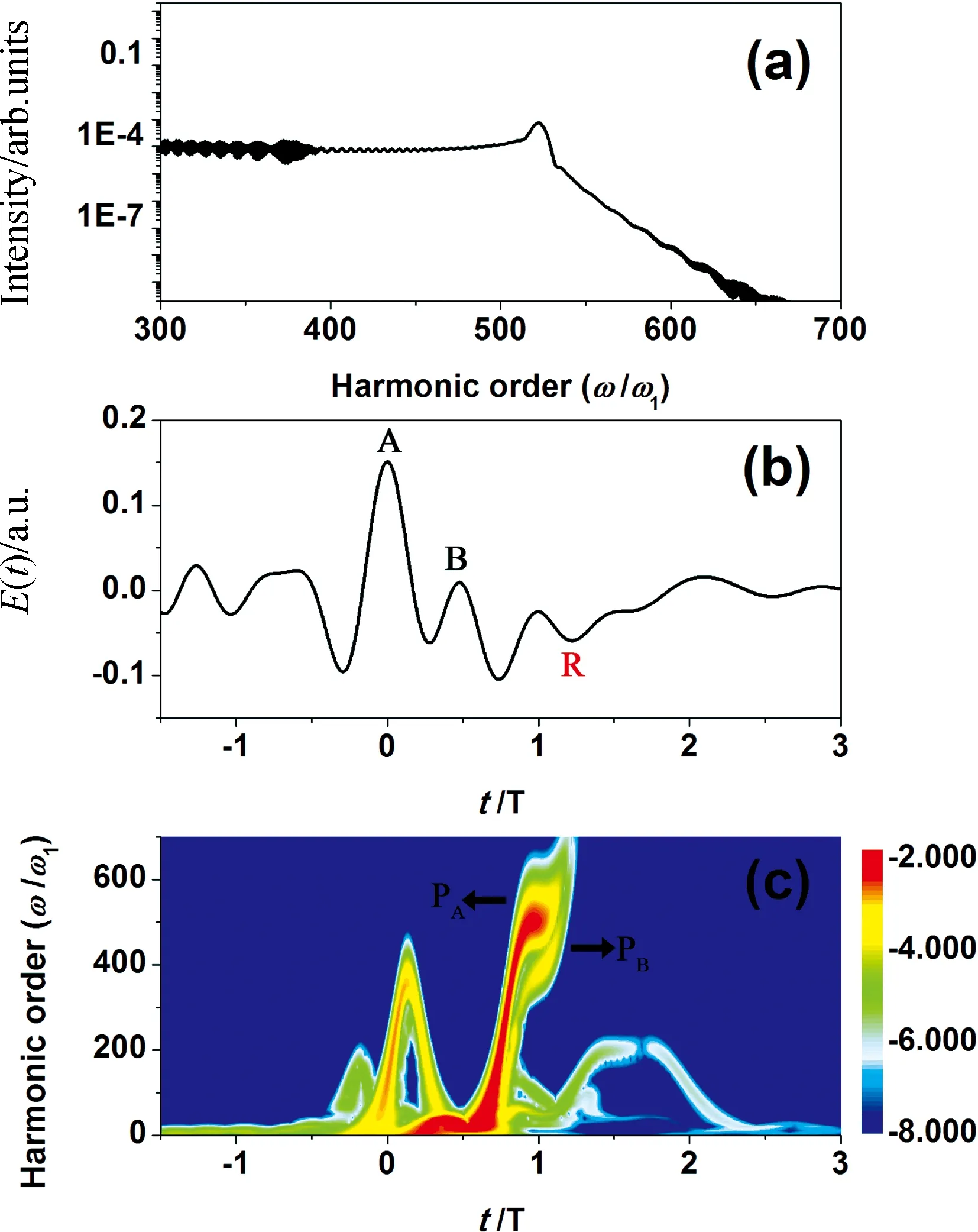
图1 (a)双色场啁啾场下谐波光谱图; (b)(c) 激光波形和谐波辐射时频分析图

图2(a)和2(b)给出了改变基频场和控制场强度时谐波辐射谱图. 如图2(a)所示,随着基频场强度增大,单价谐波增强现象消失了. 但是,随着控制场强增大,单价谐波增强比率呈现先增大后减小的现象,如图2(b)所示. 并且,在I2=2.6×1014W/cm2时,单价谐波具有最大的增强比率. 具体来说,当I2=2.6×1014W/cm2时,第529次谐波比谐波平台区其他谐波强度增大15倍.

图2 激光强度对单价谐波增强的影响：(a) 基频场强度; (b) 控制场强度

为了理解单价谐波增强比率的不同,图3和图4给出了不同激光强度下的激光波形以及在该激光场下谐波辐射的时频分析图. 首先,对于基频场强度增强的情况[图3(a)～3(b)表示I1= 2.5×1014W/cm2的情况,图3(c)～3(d)表示I1=3.0×1014W/cm2的情况],随着激光强度的增大,激光包络中反向波包的振幅大小逐渐减小[图3(a)和3(c)中箭头所示区域]. 因此,在谐波辐射过程中没有明显的折叠区域,如图3(b)和3(d)所示. 这是导致单价谐波增强现象消失的原因. 其次,对于控制场强度增强的情况[图4(a)～4(b)表示I2= 2.6×1014W/cm2的情况,图4(c)～4(d)表示I2=3.0×1014W/cm2的情况],谐波辐射能量峰PA依然存在叠加区域,如图4(b)和4(d)所示. 这是导致单价谐波增强的原因. 随着激光强度增大,A点和B点的激光振幅强度要比图1(b)中的有所增强. 具体来说,当I2= 2.0×1014W/cm2时EA= 0.15 a.u.,EB= 0.009 a.u. [见图1(b)]; 当I2= 2.6×1014W/cm2时,EA= 0.161 a.u.,EB= 0.017 a.u. [见图4(a)]; 当I2=3.0×1014W/cm2时,EA= 0.167 a.u.,EB= 0.021 a.u.[见图4(c)]. 因此,谐波辐射能量峰PA和PB的强度与图1(c)中相比都被增强,这是导致单价谐波增强比

图3 改变基频场强度下激光波形和谐波辐射时频分析图：(a)～(d)I1=2.5×1014W/cm2; (c)～(d)I1=3.0×1014W/cm2 Fig.3 The laser profiles and the time-frequency analyses of HHG for the cases of changing fundamental pulse intensity: (a)～(b) I1=2.5×1014W/cm2 and (c)～(d) I1=3.0×1014W/cm2

图4 改变控制场强度下激光波形和谐波辐射时频分析图：(a)～(b)I2=2.6×1014W/cm2; (c)～(d)I2= 3.0×1014W/cm2Fig.4 The laser profiles and the time-frequency analyses of HHG for the cases of changing controlling pulse intensity: (a)～(b) I2= 2.6×1014W/cm2 and (c)～(d) I2= 3.0×1014W/cm2

率增大的原因. 但是,当I2=3.0×1014W/cm2时,PB较强的强度会导致PA和PB能量峰干涉减小现象的增大,这是导致单价谐波增强现象减小的原因. 这与本文在图1中分析的结果一致.

本文理论研究了激光强度对单价谐波增强范围的影响. 计算结果表明：随着基频场强度增大,单阶谐波增强逐渐消失. 随着控制场强度增大,单阶谐波增强强度呈现先增大再减小的现象. 分析结果表明：单阶谐波增强不仅来源于谐波辐射能量峰的折叠区域,并且与多重谐波辐射能量峰的干涉有关.