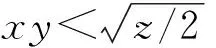On a problem of Lazar on unit fractions

, ,

(1. School of Mathematics,Sichuan University,Chengdu 610064,China; 2. School of Mathematics and Statistics,Southwest University,Chongqing 400715,China; 3. School of Science,Xihua University,Chengdu 610039,China)

Abstract: Let n be a positive integer. The well-known Erdös-Straus conjecture asserts that the positive integral solution of the Diophantine equation and (x,y)=1. Meanwhile,Lazar pointed out that it would be interesting to find an analog of this result for 5/p instead of 4/p,which is also a conjecture due to Sierpinski. In this paper,we answer Lazar’s question affirmatively and also extended Lazar’s result by showing that the Diophantine equation

Keywords: Diophantine equation; Continued fraction; Convergent; Erdös-Straus conjecture

1 Introduction

The Rhind papyrus is amongst the oldest written mathematics that has come down to us,which concerns the representation of rational number as the sum of unit fractions:

This has suggested numerous problems,many of which are unsolved,and continues to suggest new problems. One of these problems is the Erdös-Straus conjecture[1-17],which concerns the following Diophantine equation

(1)

LetNdenote the set of all the positive integers. For any positive integern,letf(n) denote the number of positive integral solutions (x,y,z)∈N3to the Diophantine equation (1),that is,

(x,y,z)∈N3}.

Then one has

f(1)=0,f(2)=3,f(3)=12,f(4)=10,

f(5)=12,….

The Erdös-Straus conjecture asserts thatf(n)>0 for alln≥2 (see,for example,[3,5]). Some related results are provided in Refs.[1,4,6-7,9-11,13].

Theorem1.1Letp≥7 be an arbitrary prime number andabe an integer with 1≤a≤6. Then there are no triple (x,y,z) of positive integers which is a solution of the Diophantine equation

(2)

Evidently,Theorem 1.1 gives an affirmative answer to Lazar’s question[12].

2 Several lemmas

For any positive integern,leta0,a1,…,anbe real numbers withai>0 fori=1,…,n. We define the finite simple continued fraction,denoted by [a0;a1,…,an],as follows:

Thek-th convergents of the continued fraction [a0;a1,…,an] is defined by [a0;a1,…,ak],wherekis a non-negative integer withk≤n.

Before giving the proof of Theorem 1.1,we need the following classical result of the theory of continued fraction which can be found in Ref.[8].

Lemma2.1[8]Letm,n,randsbe positive integers with gcd(r,s)=1. If

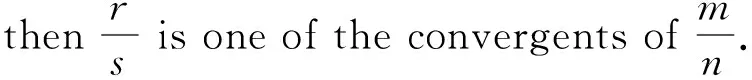
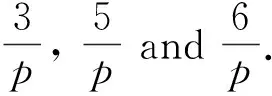
Lemma2.2Letp≥7 be a prime number. Then each of the following is true:

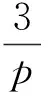
(a) Letp≡1 (mod 3). Then by the Euclidean algorithm,we obtain that

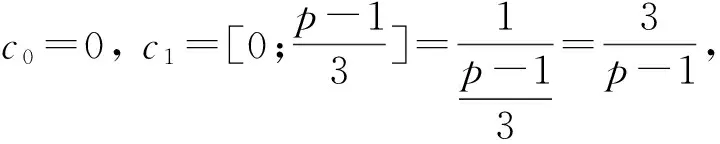
(b) Letp≡2 (mod 3). Then we deduce that

2=1×2+0.

and

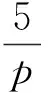
Lemma2.3Letp≥7 be a prime number. Then each of the following is true:

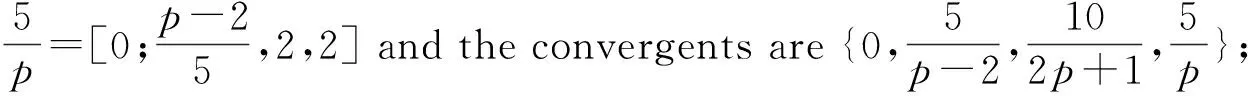
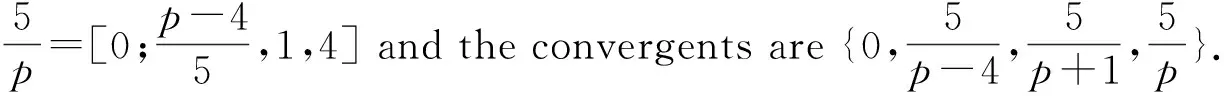
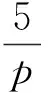
(a) Ifp≡1 (mod 5),then the Euclidean algorithm give us that

(b) Ifp≡2 (mod 5),then we obtain that

2=1×2+0.

and

(c) Ifp≡3 (mod 5),then one gets that

3=2×1+1,2=1×2+0.

and

(d) Ifp≡4 (mod 5),then we deduce that

4=1×4+0.

and

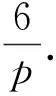
Lemma2.4Letp≥7 be a prime number. Then each of the following is true:

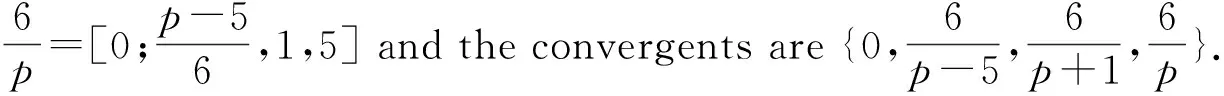
(a) Ifp≡1 (mod 6),then by the Euclidean algorithm one obtains that

(b) Ifp≡5(mod 6),then one derives that

5=1×5+0.

and

3 The proof of Theorem 1.1

According to Lazar’s result[12],Theorem 1.1 is true whena=4. So we just need to prove Theorem 1.1 for the remaining casesa∈{1,2,3,5,6}. This will be done in what follows.

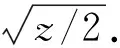
which is equivalent to the following Diophantineequation

(3)

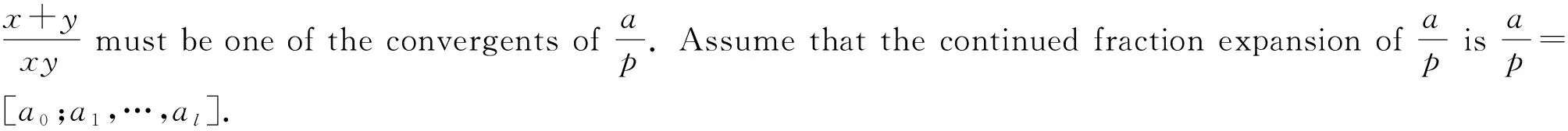
Sincexandyare coprime,x+yandxyare also coprime. Our fractions are reduced by deducing thatx+y=pkandxy=qk. The fact that suchxandymay exist relies on the solvability inNof the following quadratic equation

X2-pkX+qk=0.

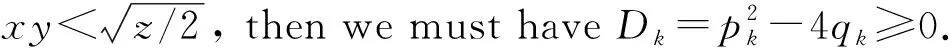
Case2a=2. Sincepis a prime withp≥7,we havep≡1(mod 2). By Euclidean algorithm,one deduces that

Case3a=3. After reducing all the fractions in Lemma 2.2,we obtain that

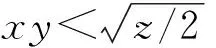
Case4a=5. By using Lemma 2.3,after reduced all the fractions,we deduce that

Case5a=6. From Lemma 2.4,after reduced all the fractions,we obtain that