多物理场耦合仿真对流在微波加热中的作用机理研究

杜知了， 吴 喆， 甘伟伟， 曾葆青

(1.电子科技大学物理学院， 成都 610054; 2.电子科技大学电子科学与工程学院·示范性微电子学院， 成都 611731)

1 引 言

液体或气体中的对流是生活中很常见的一种物理现象，蒸煮等底部加热的烹饪方式就是通过热对流作用实现对食物的加热.这是由于液体底部先受热的部分温度升高，引起密度梯度发生变化.此时底部密度相对小于上半部，则将在重力作用下形成自然对流[1-6].液体或气体中，较热的部分上升， 较冷的部分下降，循环流动，互相掺和，最终使温度趋于稳定[7].实际上对流是有物质流动参与的热传导，由于物质流动，增大了液体/气体中的传热能力，比单纯的液体/气体导热的传热能力强，因此热对流是液体的主要传热方式[8-10].

近几年来，厂家设计的微波炉时大多采用将耦合窗置于微波谐振腔的底部的方案.在生活中总会出现经过该类型微波炉加热的水或者牛奶等液态食物内部总会出现温度分层的现象，即上面热下面冷.然而对比电热器等底部加热的方式，并没有出现此类现象.因此采用液体热对流的观点去解释这种现象并不能成立，而且到目前为止，尚未看到国内外有关的研究报告.本文使用多物理场仿真软件COMSOL Multiphysics模拟了微波加热和电热器等加热一杯水的过程，集成流场，电磁场与热场相互协同作用，弥补了单一电磁仿真软件(如HFSS)只能考虑电磁场的效应而忽略多种物理热场耦合的不足[11].通过对比分析两者加热时水中温度分布的变化情况，从宏观的角度去解释产生微波加热液体分层现象的机理，希望能为微波炉的设计与优化提供新的思路.

2 多物理场模拟的物理基础

微波炉中的电磁场分布可由麦克斯韦方程可得[12]

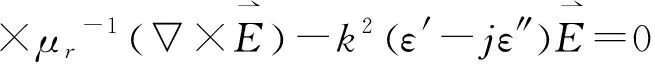
(1)

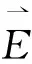
(2)

其中，Pv是微波损耗.电磁能转化为热能后可以实现对食物等介质的加热.所以Pv为传热方程的热源项.

(3)

其中，ρ是流体密度；Cp为恒压比热容；T为温度；k为导热系数.液体中对流是通过自身各部分的宏观流动实现热量传递的过程.液体先受热的部分温度升高，引起密度梯度发生变化，然后引起液体的流动.

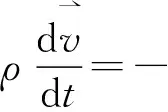
(4)

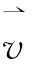
3 多物理场仿真

本文中，在COMSOL中建立简化的微波炉仿真模型，其尺寸为267 mm×270 mm×188 mm.微波通过位于腔体底部的矩形波导后，经过耦合窗馈入谐振腔，功率设置为500 W，电磁波的模式为TE10.负载采用装有500 mL水的玻璃水杯(底部半径35 mm，顶部半径45 mm，厚度为1.3 mm)，玻璃转盘(半径122.5 mm，厚度6 mm)，如图1所示 .玻璃杯和水的初始温度都为室温20 ℃，加热时间60 s.此外，为了进一步研究微波加热中对流的影响，本工作中设置了一个对照仿真模型：把水假设为固体，即加热物为具有与水相同的电磁和热学特性的“固体”，没有对流的影响.

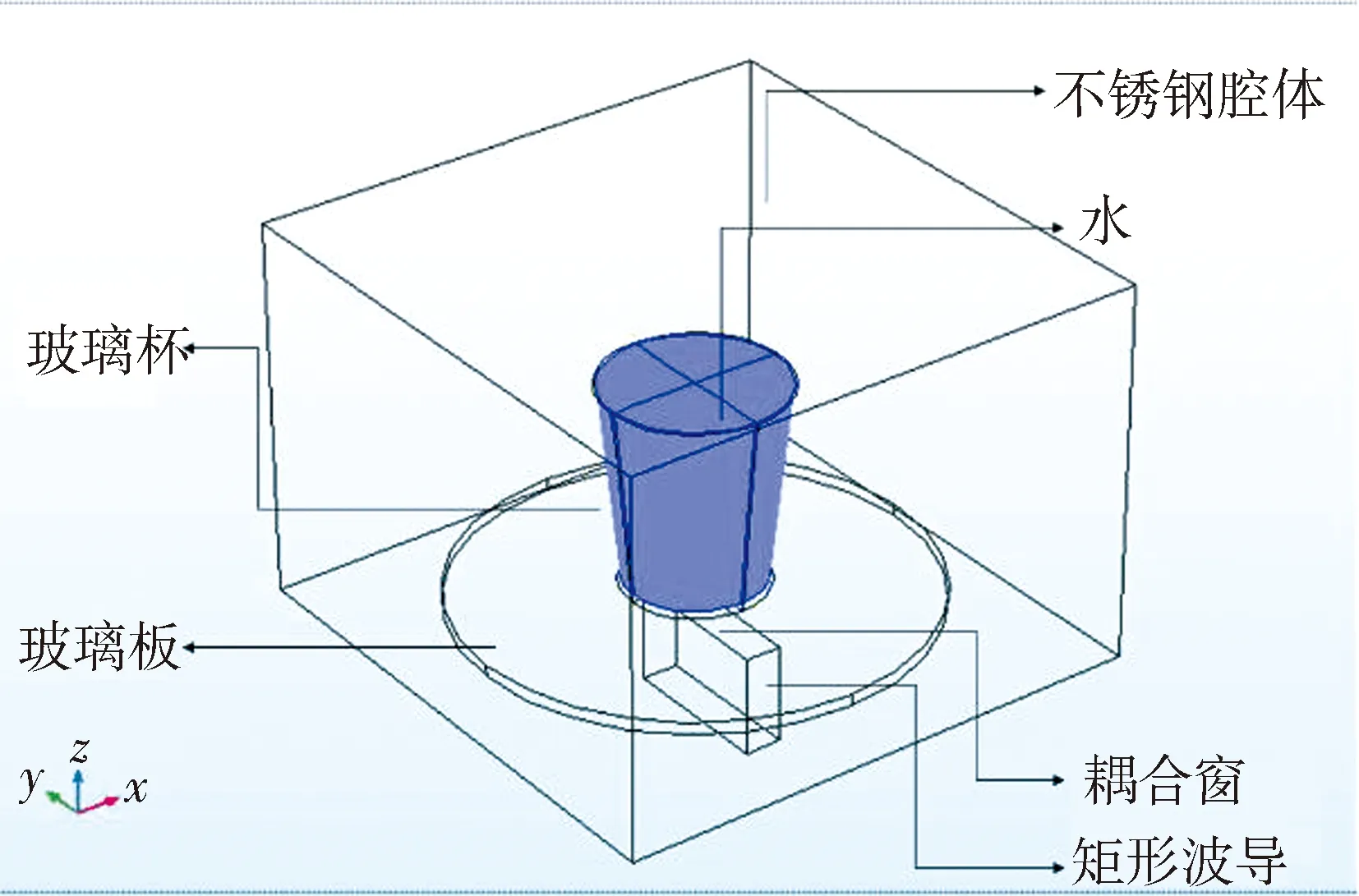
图1 微波加热几何模型Fig.1 Geometric model of microwave heating

多物理场的本质是一组偏微分方程，同时COMSOL Multiphysics是以有限元法为基础，通过求解偏微分方程(单场)或偏微分方程组(多场)来实现对物理场的仿真.在实际情况中微波炉不锈钢加热腔组分复杂而且厚度不均匀，在软件中无法精确建模.所以我们将微波炉腔体假设为具有与不锈钢或搪瓷相同物理参数的无厚度的面边界.

对于电热器等底部加热方式模型，使用与上述相同尺寸玻璃杯和等量的水.假设玻璃转盘表面与玻璃杯底面之间为理想接触，由于顶面和外表面与空气接触，使用对流热通量边界条件.为了便于仿真，我们将加热源抽象为设置在底部的恒定为200 ℃的温度边界条件，加热时间为90 s.

4 电热器加热方式仿真结果

从加热30 s，60 s和90 s时刻的温度分布来看(如图 2)，加热到30 s时，水杯底部靠近热原部分温度先升高，而远离热源的上半部区域依旧维持在20 ℃左右.于是下部水的密度变小，在重力作用下开始逐渐向上半部区域流动，同时上半部低温水向下流动.到60 s时刻，由于上下部高温水的向上流动过程中，上半部区域的温度已经升高到25 ℃左右.随着时间的增加，杯中的水循环流动，互相掺和，到90 s时，上半部温度达到28℃左右，水的最顶部出现了温度为32 ℃的2 mm薄层，温度分布呈现“三明治”的状态，但由于顶端温度较高区域极小，实际使用过程中常常无法感知.从整个过程来看，在对流的影响下，底部温度先升高，然后带动上半部温度升高，最终温度趋于平均.

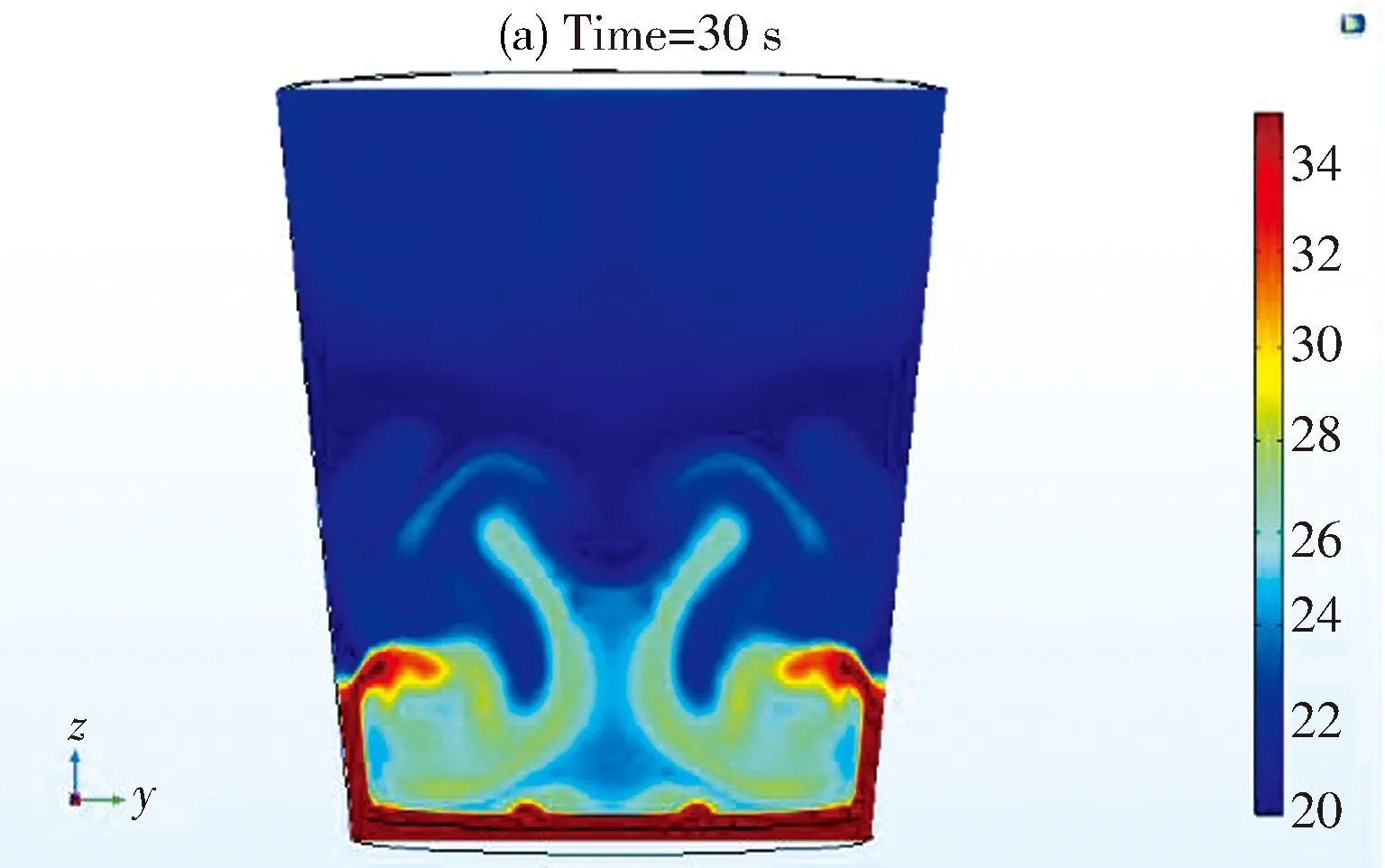
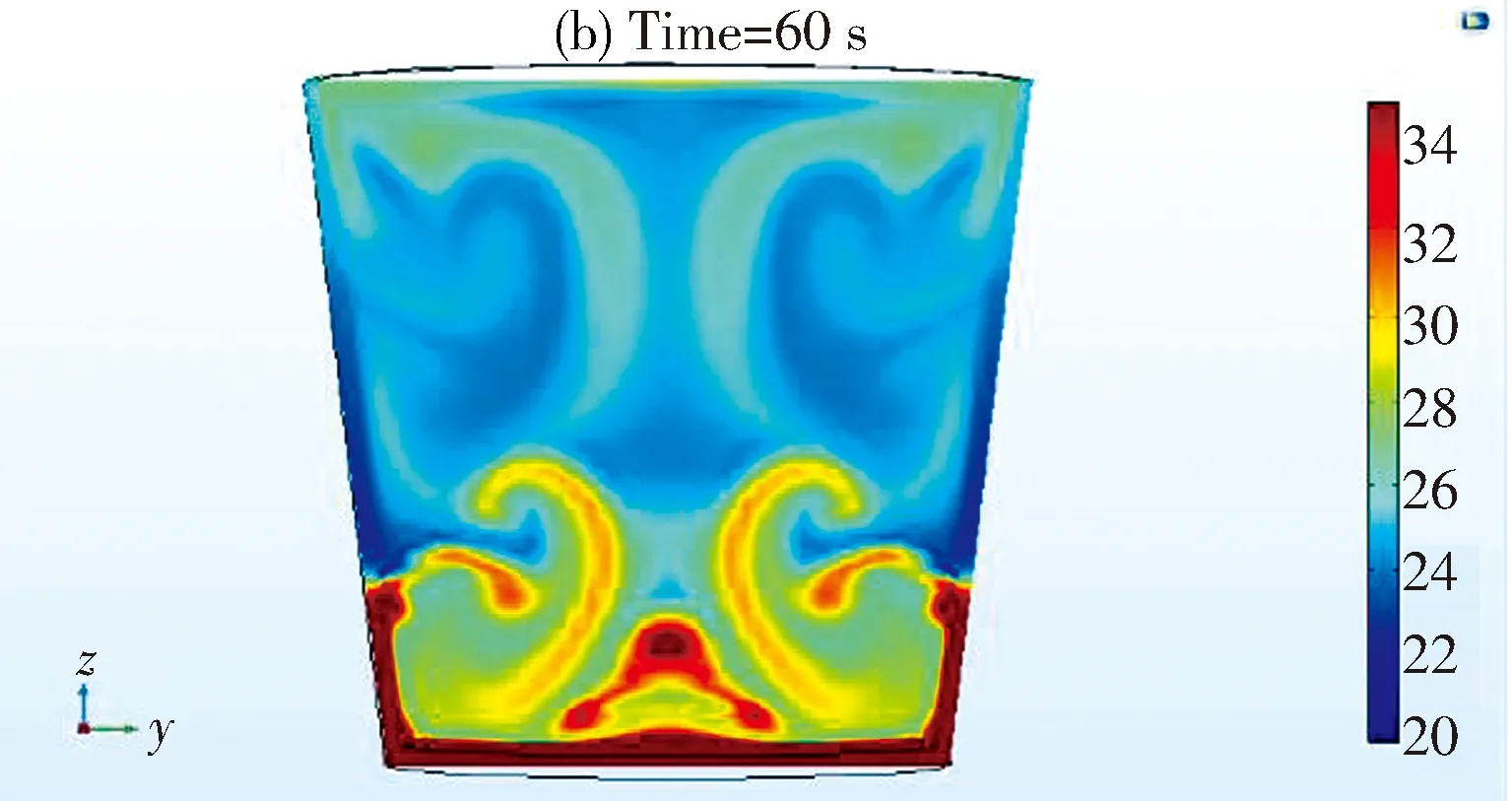
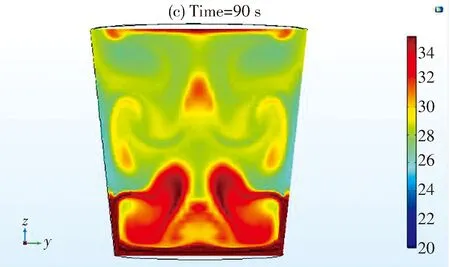
图2 等时间间隔的温度分布

5 微波加热仿真结果

图3是微波加热时不考虑对流的影响，即把水假设为固体时的仿真结果.水中的电场分布呈现出周期性的电场强弱变化，这是由于微波在水中的相对波长为

(5)

(a) 电场分布

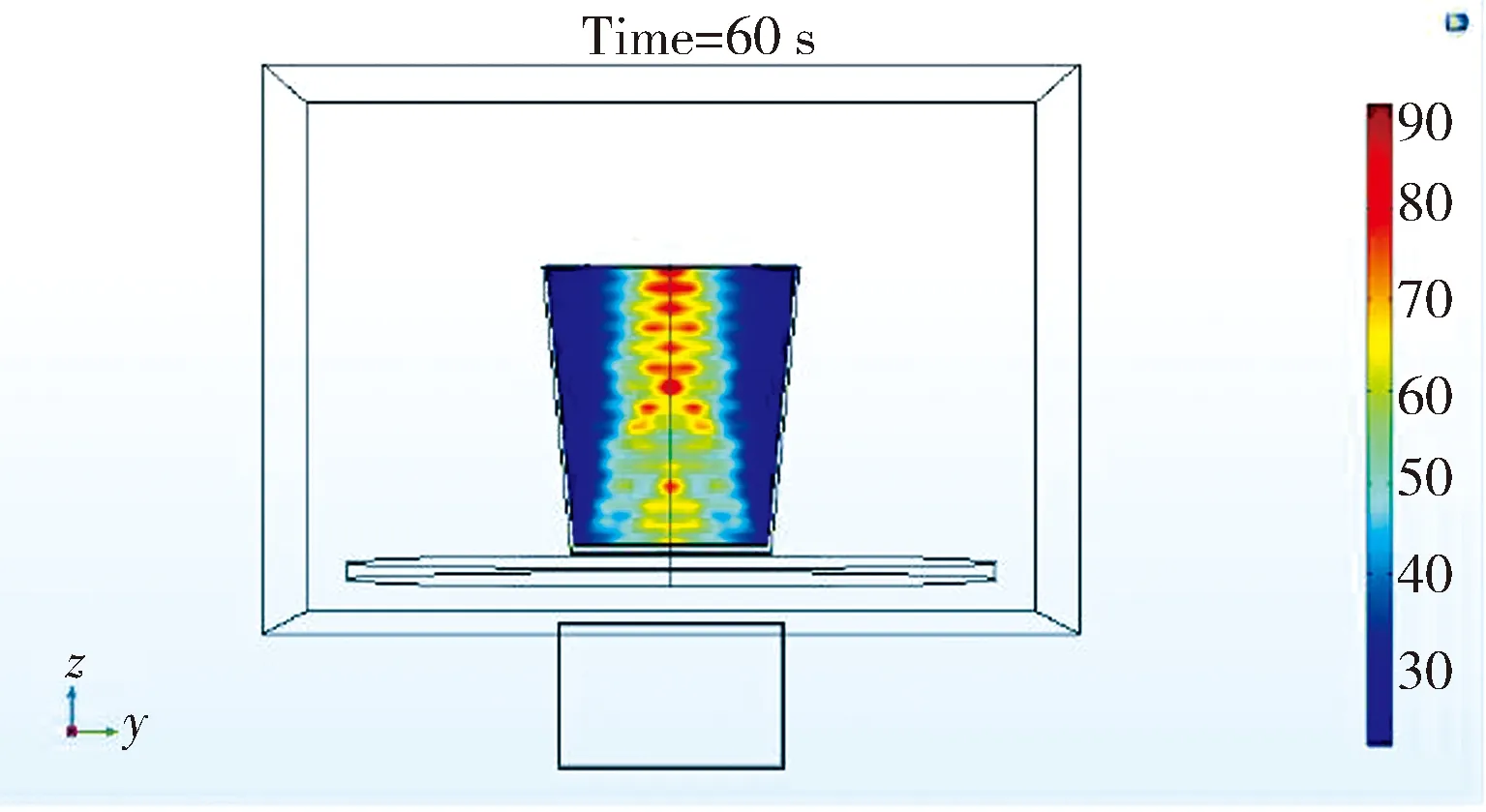
(b) 温度分布

如图3(a)，温度在50 ℃以上的区域主要集中在水的中线附近，其中上半部区域温度超过70 ℃的高温热点较多，而其他区域温度并没有明显的升高，说明没有对流的作用下微波加热均匀性较差.

图4是模拟实际的微波加热水的仿真结果.从图4(b)可以看到，微波加热水60 s后，杯子中水的温度出现了自上而下的分层现象，顶部温度最高达到了35 ℃以上，底部却在32℃左右，最大温差接近4 ℃.对比图3(b)，说明对流使水中的温度分布更均匀.这是由于整个加热腔内位于水杯顶部电场较强如图3(a)与图4(a)，所以同一时刻上半部区域水吸收的功率强于其他区域，因此水中温度最先升高的区域位于水的上半部.如果此时存在对流作用，加热过程局部的温度率先升高就会引起对流.但是根据对流的形成原理可知：(1) 局部的温度差引起密度的差异；(2) 存在高度差，才能使密度不同的区域在重力作用下发生上下流动.所以在微波加热水的过程中，上半部分的温度始终要高于下部分的温度，因此上半部分水的密度略大于下部.所以只是局部区域的相对流动，没有自下而上的对流，最终出现了如图4(b)所示的温度分层现象.这也可以解释为什么微波炉加热水容易出现暴沸现象：传统的烧水方式都是下方加热，在加热过程中会有自下而上对流，水中的空气泡在上升的过程中起到了搅拌作用，到达正常沸点时，蒸汽压力等于外压，水就很平稳的沸腾，不会产生暴沸[13].

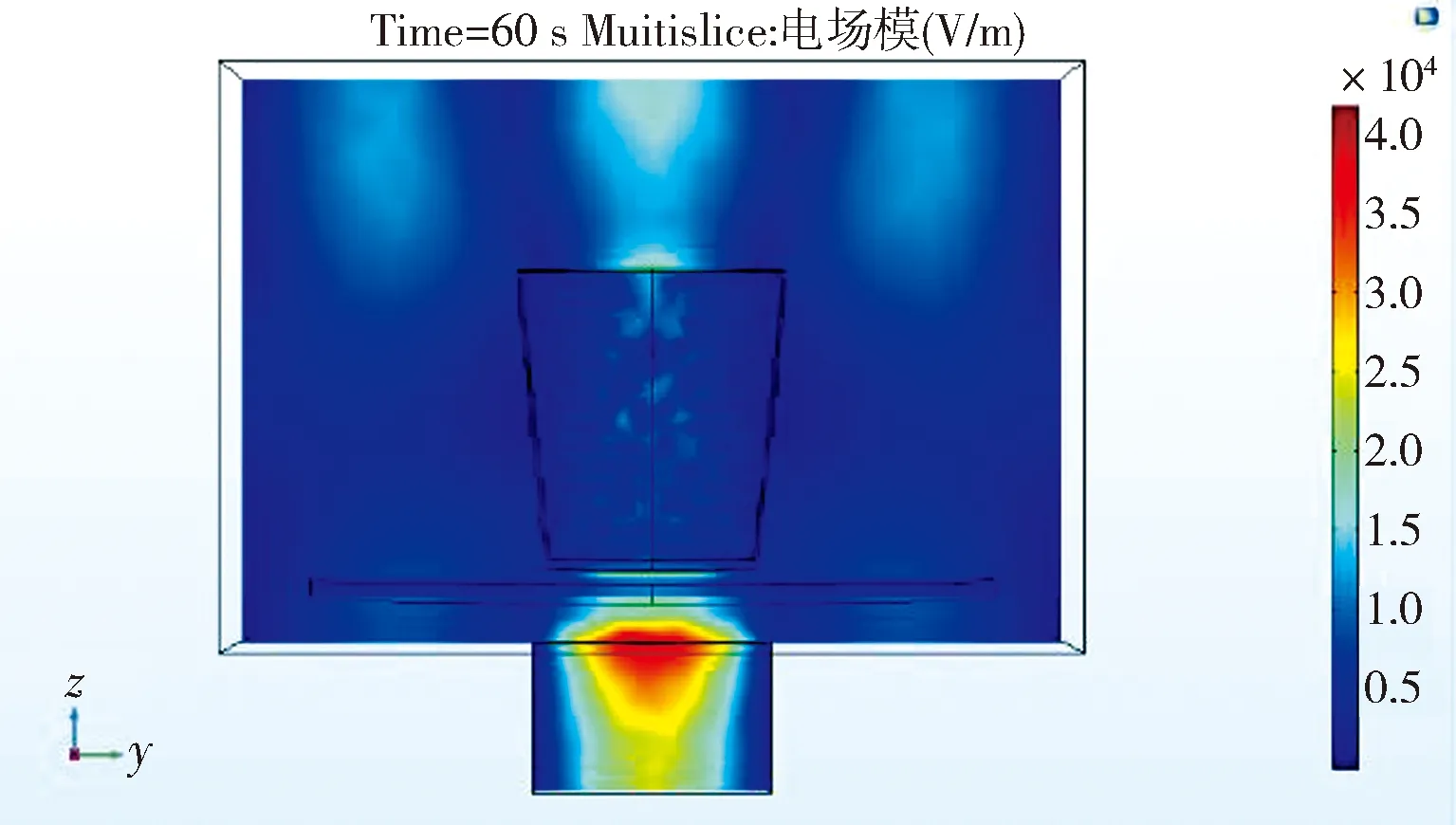
(a) 电场分布

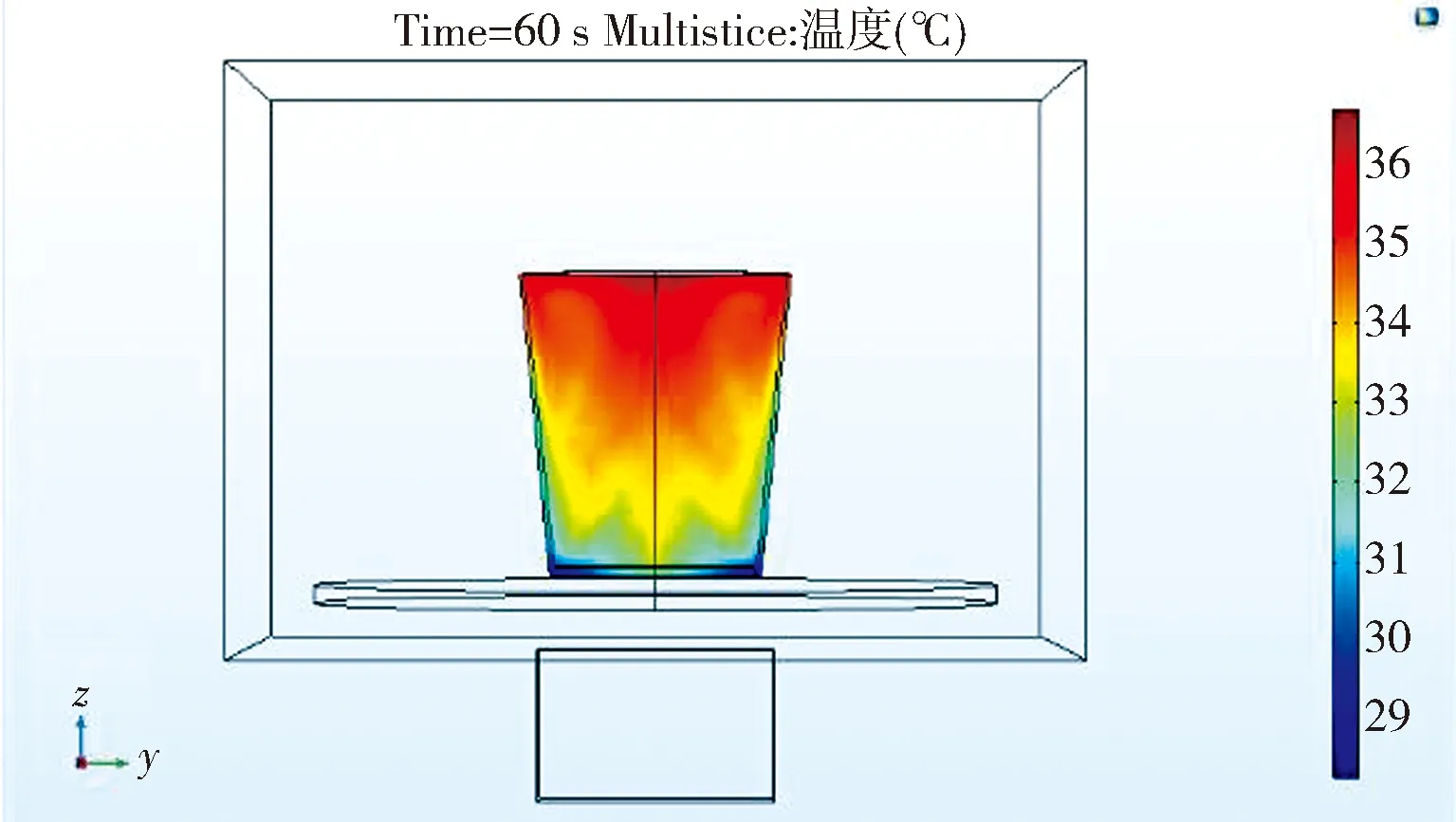
(b) 温度分布

对比图3(a)与图4(a)可知，尽管对流可以引起水中局部温度的变化，但是对电场的分布影响较小.这是由于在相同的时间内对流引起的温度变化对介电常数影响较小.

6 结 论

家用微波炉就是一个典型的微波谐振腔，炉内的电磁场分布不均匀，在加热的过程中局部温度快速升高，在这种情况下热对流现象会变得比传统加热方式更复杂和不确定，因此不能运用电热等底部加热方式中的热对流去解释微波加热中的对流现象.本文通过多物理场的仿真计算，模拟了微波与电热器等底部加热的方式在加热杯中水的情况，通过分析对流现象对电场与温度分布特性的影响得出：对流对微波腔内的电场分布影响较小；微波加热杯子等容器盛装的液体时，微波加热水的过程中，上半部分的温度始终要高于下部分的温度，因此产生局部区域的相对流动，并非电热器等加热方式中的自下而上的对流，最终导致微波加热的液体中出现温度上下不均匀的温度分层现象，而且上下部分的最大温差接近4 ℃.