导叶开度对混流式水轮机转轮应力应变的影响

2020-12-04史广泰朱玉枝刘宗库李金

排灌机械工程学报 2020年11期

史广泰，朱玉枝，刘宗库，李金

(1. 西华大学流体及动力机械教育部重点实验室，四川成都 610039; 2. 西华大学能源与动力工程学院, 四川成都 610039)

混流式水轮机适应水头范围广,结构紧凑，转轮效率较高，被广泛应用于水电站.水轮机转轮由于受到流固耦合作用的影响容易发生变形，从而造成水轮机转轮叶片出现裂纹和断裂等问题，这将严重影响水轮机机组的安全稳定运行.

目前已有较多学者对水轮机转轮内的流固耦合特性进行了研究.文献[1-2]研究了不同工况下水轮机转轮叶片应力分布情况，以及应力及应变的变化规律.文献[3-4]通过对水轮机的转轮进行数值计算，得到其应力与位移分布位置及最大值随水头变化的规律.肖若富等[5]分析比较了转轮的应力和变形值，得到引起单、双向耦合计算结果差别的重要因素是变形量大小.郑小波等[6]基于双向流固耦合，对贯流式水轮机进行数值计算，得到耦合作用降低了转轮水力性能，与考虑单向流固耦合情况相比其等效应力的分布一致.文献[7-8]利用双向流固耦合方法，研究了耦合作用下混流泵和核主泵叶轮的力学特性.文献[9-11]基于流固耦合对混流式水轮机进行数值计算，得到了不同工况下转轮的动应力特性，进而分析了叶片产生裂纹的原因并提出一些对策.文献[12]研究得到了水轮机转轮叶片在水力激励下的疲劳裂纹扩展规律.文献[13-14]通过对水轮机进行数值计算，研究得到其应力的分布情况.

由于实际运行过程中固体变形对流体的影响极小，故文中主要通过研究总结转轮变形和应力的分布情况以及变化规律，并将计算结果与转轮实际破坏位置进行比较.

1 理论基础

1.1 数值计算基本方程

水轮机内部的流体流动必须满足连续性方程、动量方程[15]等，具体如下.

连续方程：

(1)

动量方程：

(2)

其中Suj为附加源项，而

(3)

1.2 流固耦合计算基本理论

Newmark时间积分法的具体方程为

(4)

(5)

由式(4)—(5)可得

(6)

(7)

ut+Δt可根据t+Δt时刻的运动方程求得，即

(8)

式中：M，C，K，F分别为结构总体质量矩阵、结构阻尼矩阵、结构的总刚度矩阵、作用在节点上的外载荷向量.

2 研究对象

选择一混流式水轮机作为研究对象，其主要参数：水轮机型号为HLD307-LJ-290，转轮直径为2.93 m，转轮叶片数为15，活动导叶数和固定导叶数均为20；最高水头为184.0 m，额定水头为159.3 m，最低水头为145.7 m，额定流量为62.7 m3/s，额定转速为272.7 r/min，额定出力为92.3 MW，最大出力为107.0 MW，最大吸上高度为-3 m.

在最低水头、额定水头和最高水头时对混流式水轮机3种导叶开度(40%，70%和100%)下转轮的应力应变特性进行数值计算.

3 网格划分和边界条件设置

采用三维建模软件对水轮机各过流部件进行三维建模，其三维模型包括各个过流部件的水体模型和结构模型.所建立的水轮机过流部件的三维几何模型如图1所示.然后对所建立的模型进行网格划分，并进行网格无关性验证，确保网格满足计算要求.图2为最终划分的网格，网格数为5.0×106.

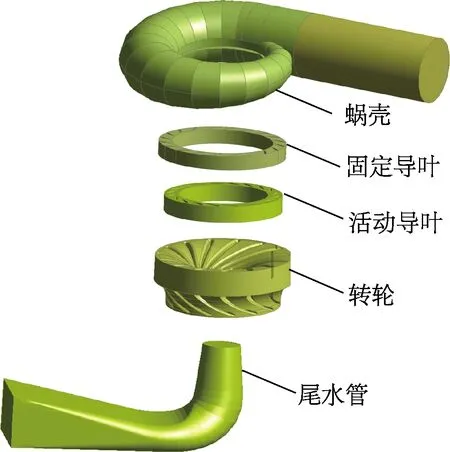
图1 水轮机三维几何模型

图2 水轮机过流部件网格划分

基于单向流固耦合的方法，采用standardk-ε湍流模型和Scalable壁面函数，运用ANSYS CFX软件对混流式水轮机过流部件进行数值计算，计算时首先对水轮机进行定常计算，然后以其结果作为非定常计算的初始值进行非定常相关数值计算.在数值计算时设置进口为总压进口，出口为静压出口，壁面为无滑移壁面，工作介质为纯水.在进行非定常计算时，时间步长设为1.833 52×10-3s,即以转轮每转过3°的时间为1个时间步长.计算收敛后，取最后1个周期进行分析.残差收敛标准设置为10-5，当计算残差小于10-5时，即认为计算收敛.转轮转速设为272.7 r/min，方向同z轴，转轮受到来自流体的压力，其大小直接由流场计算结果导入.

转轮叶片材料为ZG06Cr16Ni5Mo不锈钢，具体参数为密度8 g/cm3，弹性模量210 GPa，屈服强度600 MPa，泊松比0.3.

4 转轮现场破坏分析

图3为现场所拍摄到的混流式水轮机转轮破坏位置.

图3 混流式水轮机转轮实际破坏位置

由图3可见，混流式水轮机转轮叶片发生破坏的主要位置位于转轮叶片出口靠近下环以及与泄水锥交接处.为了分析该转轮叶片出现破坏的机理，采用数值计算方法在不同导叶开度下对该机组进行流固耦合计算.

5 计算结果分析

5.1 水轮机转轮瞬态变形分析

图4为额定水头下水轮机转轮不同导叶开度λ时的瞬态变形图，图中δ为变形量.由图可知：在不同导叶开度下，水轮机转轮叶片瞬态较大变形主要分布在叶片出水边中部，且随着导叶开度逐渐增大，转轮叶片出口中部的最大瞬态变形量也逐渐增加，且最大变形区域逐渐增大；下环处的变形量大于上冠处，在40%开度下，叶片表面变形不均匀，随着导叶开度增大其变得更加均匀.通过局部放大图还可见，在所选不同开度下叶片出口边均发生了明显的变形.

图5为水轮机转轮最大变形图.由图可知，同一水头下，随着导叶开度增大，水轮机转轮叶片最大瞬态变形逐渐增加.由图还可见，在同一导叶开度下，随着水头增加，水轮机转轮叶片最大瞬态变形逐渐增加.

5.2 应力分析

图6为额定水头下水轮机转轮不同导叶开度时的最大主应力σmax分布图.由图可知，在40%开度下，最大主应力主要集中在水轮机转轮叶片出水边靠近下环处和叶片出水边与泄水锥交界处.由图3可知，在运行情况下叶片出水边靠近泄水锥处出现贯穿性裂纹的位置与最大主应力较大位置刚好对应.下环所受应力大于上冠处所受应力，且随导叶开度增大其不均匀程度增大.

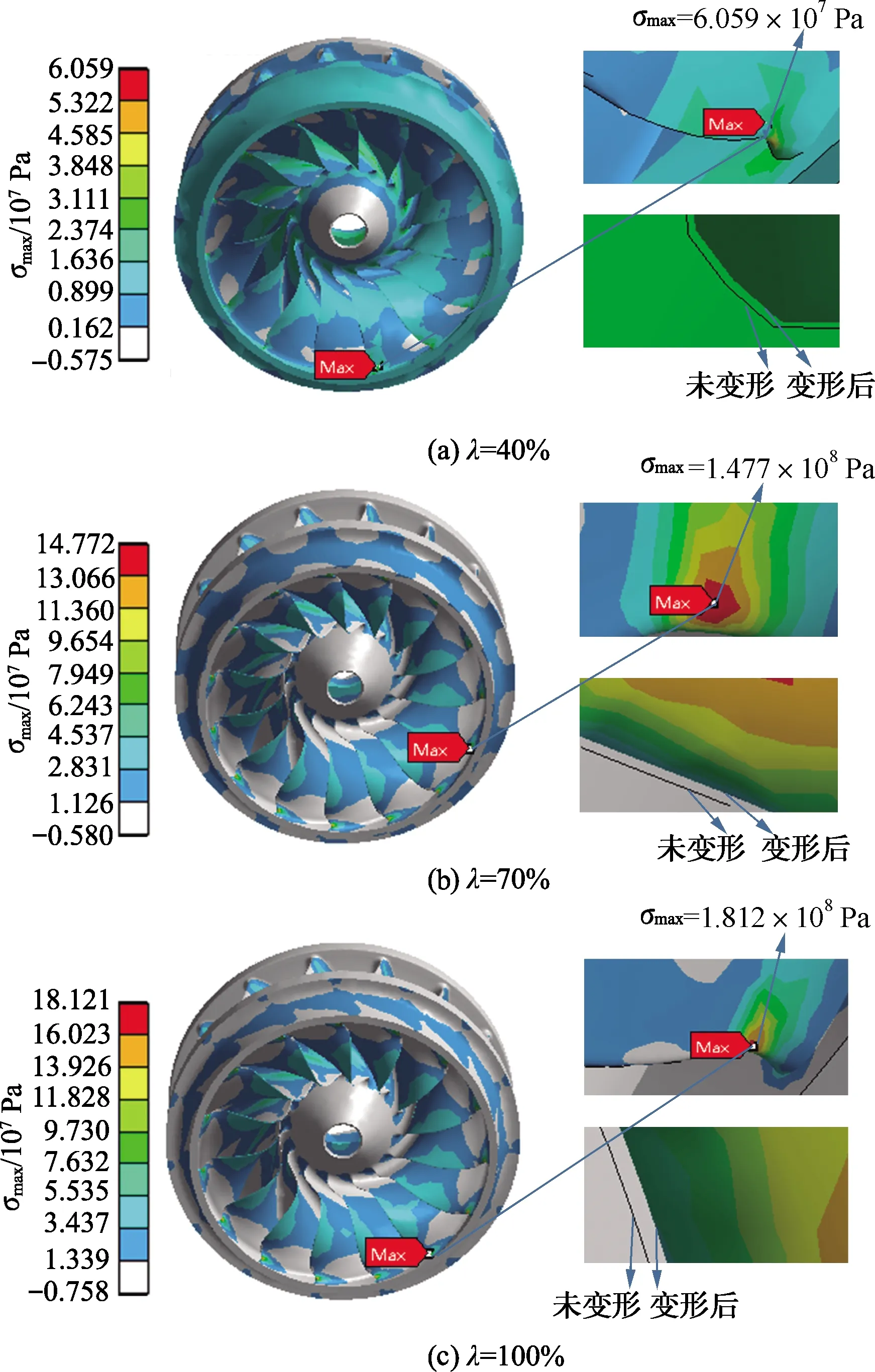
图6 水轮机转轮最大主应力

由图6还可见，随着导叶开度增大其最大主应力最大值逐渐增大.在100%开度下最大主应力最大值最大，且作用位置也位于转轮叶片出水边靠近下环处，由于转轮叶片出水边靠近下环处较叶片其他位置薄，因此较大的应力作用在抵抗变形薄弱处易出现裂纹和断裂情况，这对水轮机正常运转极为不利.

图7为水轮机转轮最大主应力图.由图可知，同一水头下，随着导叶开度增大，水轮机转轮叶片最大主应力逐渐增大.由图还可见，在额定水头和最高水头下，开度70%前的最大主应力变化率较开度70%后的大.

图7 水轮机转轮最大主应力变化

5.3 等效应力随时间变化图

图8为额定水头下水轮机转轮不同导叶开度时的等效应力σe.由图可知,在不同导叶开度下，水轮机转轮较大等效应力主要集中在叶片出水边与泄水锥交界处和叶片出水边靠近下环处，且随着导叶开度增大，最大等效应力也逐渐增大.由图还可见，下环所受等效应力大于转轮上冠所受等效应力，且随着导叶开度逐渐增大，较大等效应力分布的区域越集中.这与图3中该水轮机转轮出现裂纹和掉块的情况相一致，即该转轮发生破坏的主要原因是由于流固耦合作用的影响.

图8 水轮机转轮等效应力

图9为水轮机转轮最大等效应力σe,max图.由图可知,在同一水头下，随着导叶开度增大，水轮机转轮叶片最大等效应力逐渐增大；同一导叶开度下，随着水头增加，水轮机转轮叶片最大等效应力逐渐增大.

综合图7和9可知，在100%开度下，从最低水头到额定水头，转轮等效应力与最大主应力均增大了9.8%；从额定水头到最高水头，其增大了15.9%.

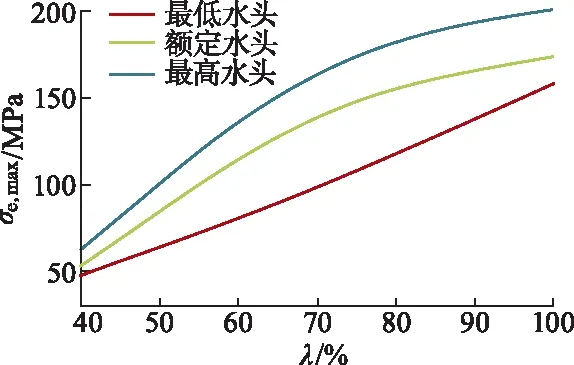
图9 水轮机转轮最大等效应力变化

综合上述分析并结合转轮叶片材料参数可知，此转轮材料为塑性材料且通过查阅文献可知该材料的屈服极限为600 MPa.在额定水头、不同开度下，水轮机转轮叶片所承受的瞬态最大主应力最大值均远小于许用应力，故水轮机转轮材料满足强度要求.不同开度下，转轮最大等效应力的最大值皆小于材料屈服极限，没有超过疲劳极限.为了避免叶片出现裂纹, 可以在叶片出水边与上冠交接处加装应力释放三角块，以降低叶片最大有效应力值、改善叶片应力分布[11].