且“形”且“真晰”

邱小珊

【摘要】初中阶段的几何学习，是学生数学基础几何学习的起步阶段：初步学会如何分析图形，联系所学图形的定义、几何性质，进行简单有序的逻辑推理去解决问题;为逐步构建完整的几何知识体系、培养严谨的几何分析能力及逻辑推理思维打下扎实的基础。

【关键词】基本模型图;阶梯式教学;知识体系;模型思想

【中图分类号】G633.6【文献标识码】A【文章编号】1992-7711（2020）32-201-02

在北师大版数学七年级下册第二章《相交线与平行线》这一章的教学中，笔者把“转化”思想、整体思想、模型思想贯穿于这一章教学的整个过程——在解题的过程中，把复杂的问题，转化为几个简单的小问题;把问题中复杂的图形、结构，转化为简单的、经典的基本图形结构，利用基本模型图的概念、性质以及相关定理等知识，清晰、快速地解决问题，让学生对直线的位置关系有了一个由浅入深的阶梯式的认识，帮助学生从“模型思想”的角度完整地构造几何知识体系。这样的学习思路和方法，降低了学生几何学习的台阶，学生在心理上很容易接受，从而解题的效率也提高了。在教学中真正做到以学生为学习的主体，贯彻课标中“基础教学”的指导思想。

初中阶段的几何学习，是学生数学基础几何学习的起步：初步学会如何分析图形，联系所学图形的定义、几何性质，进行简单有序的逻辑推理去解决问题;为逐步构建完整的几何知识体系打下扎实的基础。所以，如何有效学习初中阶段的几何基础知识，打好几何学习的入门基础，尤为重要。

一、为什么要重视几何知识中的基本模型图

平面几何是研究平面上几何图形的性质（形状、位置、大小关系等等）的数学分支，要能够有效地解决一个平面几何问题，不仅要正确地认识一些基本平面模型图及其性质，还要具有把复杂问题转化为简单、基本问题的能力——从复杂问题中挖掘出基本模型图，并运用所选的基本模型图的性质、判定等知识及方法去解决问题。学会用基本模型图的相关知识去解决问题，不仅能提高解题的效率，又能进一步加深对知识的理解，构建知识之间的联系，逐步构建完整的数学知识结构，从而提高数学素养。

例如，在七年级下册第二章《相交线与平行线》的教学中，紧扣相交线和平行的基本模型图，强调解题中转化思想的应用;在八年级下册第一章第3节、第4节《线段的垂直平分线》、《角平分线》的教学中，强化垂直平分线和角平分线性质的基本模型图及模型思想，降低起点，根据我们学生的实际学情——基础差，图形分析能力差，确定这样的出发点是很适合的，避免了学生在几何解题方面无从下手的尴尬局面。平行线、垂直平分线、角平分线的性质是几何学习里面很重要的基本性质，是后面学习全等三角形、平行四边形、相似三角形、圆等几何知识的重要基础。

本文将简单总结关于《相交线与平行线》、《垂直平分线》、《角平分线》这三课的课堂教学指导。

二、基本模型图的相关知识

笔者认为文献中对基本图形的相关知识的总结比较全面。

图形作为几何学科的研究对象，无论多么复杂，都是由一个或者若干个最简单的、最基本的图形组合而成，找到这些基本图形往往也就找到了解决问题的突破口。那什么是基本图形呢？笔者参考了以下几种理解：

1. 基本图形的几种看法

（1）埃及人把正方形、矩形、三角形和梯形作为基本图形;

（2）认为基本图形是课本上一些重要的定理或者重要练习所对应的图形（如切割线定理、割线定理和射影定理等图形）;

（3）认为现行初中几何课本中的概念、性质、例题、习题所对应的图形可视为平面几何基本图形;

（4）认为现行初中几何课本中一些具有广泛应用的、有代表性和典型性的图形可称为基本图形;

（5）认为凡是与几何定理相关的图形都是基本图形;

（6）认为现行中学平面几何课本中概念、定理、公理所对应的图形都称为基本图形，它們可分为第一类和第二类基本图形。所谓第一类基本图形，是指点、直线、射线、线段、角、相交线、平行线、三角形、四边形、多边形和圆等，其余的则称为第二类基本图形。

参考以上几种看法，我认为，基本图形，就是在几何问题中，组成一个几何问题的最简单的、最基本的，但又最重要的，且具有特定性质的，或者可以独立形成概念的，能明确阐明应用条件和应用方法的图形。

2.基本图形的分类

基于不同的分类标准，基本图形也有许多不同的分类方法：

第一类，现行教材中概念、公理、定理以及推论所对应的图形（如点、直线、射线、线段、角、相交直线、平行线、三角形、四边形、多边形和圆等）;

第二类，教材中具有一定典型性的例题、习题所对应的图形，也可以说是若干个第一类基本图形的组合（如“X”型，“A”型，“三线八角”， 直角三角形及其斜边上的高，三角形及其角平分线，平行四边形及其对角线，垂径定理及其推论，圆内接四边形及其对角线，圆及其切割线，圆的相切或相交等）， 在实际教学中教会学生挖掘这些基本图形的结构性质并运用其性质解决问题具有重要的实践性意义。

三、相交线与平行线的“基本模型图”的教学思路

在七年级下册第二章《相交线与平行线》的基本模型图，是以平面中直线的两种位置关系来展开讨论的：相交线的基本模型图（一般的相交、特殊的相交即垂直），平行线的基本模型图（“三线八角”、同位角、内错角、同旁内角）。直线的这两种位置关系的基本模型图，是本章学习的基础，更是几何解题的重要基本模型，对于系统学习几何，培养图形分析能力、逻辑推理能力、深化模型思想的理解及运用都有重要的启发作用。

下面，笔者将展示这两种基本图形，以及如何进行清晰有效的教学引导。

1.两直线相交的基本模型图的教学思路

（1）相交线的定义：若两条直线只有一个公共点，称这两条直线为相交线。

（2）根据这个定义，就可以画出相交线的基本模型图如下：;;

（3）研究相交线，形成基本概念、掌握性质：

①在这个基本的几何模型中，基本的幾何元素（图形）有：一个交点（点O）;两条直线（直线AB，CD）;四个角（∠AOD;∠AOC;∠BOD;∠BOC）;

②位置关系：直线AB与直线CD相交;

③相关性质：四个角的位置关系、数量关系的探讨：引出对顶角的概念（对顶角的位置关系和数量关系）、余角和补角的概念以及性质;通过对这些角进行定性和定量的探索，深刻了解两直线相交的性质并得到巩固。

④由抽象到具体：特殊的直线相交关系：互相垂直。用具体的特殊角（90度角）这一数量研究两直线互相垂直的性质。再把两直线互相垂直应用到实际问题中：过一点有且只有一条直线与已知直线垂直;通过垂直来定义：点到线之间的距离。（图形语言、数学语言可参考北师大版数学教科书七年级下册第二章）

（4）解题中基本模型图的应用：从几何图形中提炼出相交线的基本图形，再利用对顶角相等或者余角、补角的性质，解决全等或者相似的相关问题;用垂直的基本图形的性质解决几何问题和实际问题。构建完整的数学知识体系。

2. 两直线平行的基本模型图的教学思路

（1）平行线的定义：若两条直线没有公共点，称这两条直线互为平行线。

（2）根据这个定义，就可以画出相交线的基本模型图如下：（口头上我们称它“三线八角”：其中，所成的夹角之间的关系有：Z型中互为内错角，F型中互为同位角，U型中互为同旁内角）

（3）研究平行线，形成基本概念、掌握性质：

①在这个基本的几何模型中，基本的几何元素（图形）有：三条直线，两个交点，八个夹角;

②直线之间的位置关系：一组直线互相平行;两组直线相交;;

直线相交的关系在上面已经学习过，故进行下面的教学引导：

③两条平行线之间的位置关系的探讨：两直线平行这种位置关系的性质太抽象，需要通过定量来研究平行这一性质，因此引出第三条直线与原来两条直线形成相交关系，构造角这个具体的量，通过研究所成的角之间的数量关系来体现原两条直线的位置关系;反过来，两直线的平行关系这一性质又可以推理出各类角之间的数量关系。这就是平行的性质与判定。（图形语言、数学语言可参考北师大版数学教科书七年级下册第二章）

这是研究几何性质的重要方法：量的关系体现性质的关系，即量变促成质变;反过来，性质可以推理出量的关系。

（4）解题中基本模型图的应用

教学手段：引导学生在几何图形中，能用铅笔描绘（识别并提炼出）平行线“三线八角”的基本模型图，进一步分析角与角之间的位置关系和数量关系（Z型中互为内错角？F型中互为同位角？U型中互为同旁内角？），从而解决与直线性质或者角的数量有关的问题。

四、垂直平分线与角平分线的“基本模型图”的教学思路

1.线段的垂直平分线

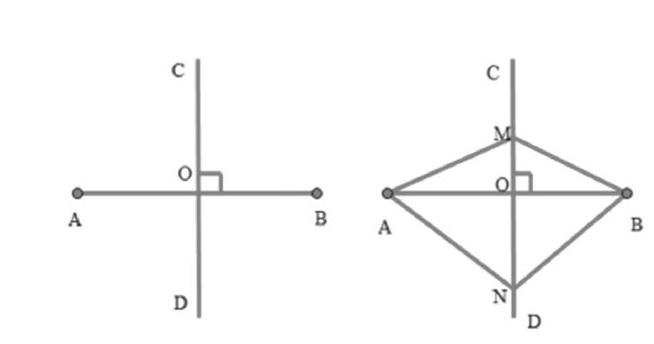
（1）基本模型图：

（2）定义：与线段垂直并平分该线段的直线;

性质：线段垂直平分线上的点到线段两端点的距离相等。

（3）线段垂直平分线基本模型图的补充推论：

①全等三角形的提炼与运用：ΔMAO≌ΔMBO;

相关知识点：全等的判定与性质等;

②等腰三角形的提炼与运用：等腰三角形ΔMAB;

相关知识点：等腰三角形三线合一等;

③直角三角形的提炼与运用：RtΔMOA等;

相关知识点：直角三角形角的性质;勾股定理;三角函数等;

（4）解题中基本模型图的应用

教学手段：几何问题中遇到线段垂直平分线，首先能快速识别基本模型图，熟练运用其定义、性质解决问题;第二是能够利用基本模型图的补充推论去解决更加综合的几何问题;第三，在提高题中，能够由此启发添加辅助线构出此模型图，从而运用性质和推论解决问题。

2.角的平分线

（1）基本模型图：;

（2）定义：平分一个角的射线;

性质：角平分线上的点到角的两边的距离相等。

（3）角平分线基本模型图的补充推论：

①全等三角形的提炼与运用：ΔDEO≌ΔDFO;

相关知识点：全等的判定与性质等;

②点到线之间的距离的提炼与运用;

相关知识点：距离的概念;

③直角三角形的提炼与运用：RtΔMOA等;

相关知识点：直角三角形角的性质;勾股定理;三角函数等;

（4）解题中基本模型图的应用

教学手段：几何问题中遇到角平分线，首先能快速识别基本模型图，熟练运用其定义、性质解决问题;第二是能够利用基本模型图的补充推论去解决更加综合的几何问题;第三，在提高题中，能够由此启发添加辅助线构出此模型图，从而运用性质和推论解决问题。

关于线段垂直平分线和角平分线的教学指导：

学生在学习的过程中，从一个简单的定义、性质及其图形开始，通过对图形的分析，把几何中相关的知识联系起来，在这样的学习过程中，知识之间的联系逐渐清晰;几何的知识系统逐渐完善，在往后几何学习、解题中对知识和方法的理解会越来越深刻、提炼知识也会越来越快。因此，笔者认为这是几何教学中有效的指导方法。

综上所述，在数学几何模块的学习中，由基本图形构成的基本模型图是学习几何的重要部分，对于基础比较差的学生，阶梯式学好基本模型图（由最简单的几何图形以及最简单的图形之间的关系图开始，逐渐过渡到重要性质的典型基本图形，逐步把几何知识联系起来，形成一个逐渐完整的几何知识体系，以整体的思维看待几何知识、几何问题），可以更好地理解几何性质和启发解题思路，进一步而言，有助于学生头脑中数学知识结构的完善以及问题解决中知识和方法的提炼，也就是数学素养的提高。

另外，基本模型图的熟练掌握，对于数学的提高也是非常关键：基本模型图是一个整体，审题有了分析基本模型图的习惯，就提高了对数学解题的整体思想的理解，这是数学的重要思想;对于难度比较大的几何题，需要作辅助线的时候，往往可以从基本模型图出发去分析、构造，得到启发，从而可以很快做出有效的辅助线构图，解决问题。

初中阶段平面几何的基本模型图不止以上几种，在课堂学习的过程中，从新知的理解到知识的运用，我们都要教会学生懂得以整体的角度去看待、理解、运用基本模型图;善于自己去总结、积累并且可以做到变式创新提高，从更高的角度去渗透每个基本模型图，提高几何解题能力及自身的数学素养。由基本模型图散发开去，最后又离不开几何知识系统这个整体。

【参考文献】

[1]高一子.基本图形在平面几何中的数学运用[ J ].陕西：师范大学出版社，2015：6.

[2]傅佑珊.平面几何基本图形的方法与教学实践[ J ]. 北京教育学院学报，1997（2）： 71.

[3] /徐方瞿.基本图形分析法[M] .基本图形分析法[ M].郑州：大象出版社，1986：1.

[4] 沈文选，杨清桃.数学史话览胜[M] .哈尔滨：哈尔滨工业大学出版社，2008：15.

[5] 桂文通.基本图形法在几何解题中的应用[J] . 数学教学通讯，2002 （10） ： 38.

[6] 李美华.平面几何中基本图形的应用[J]. 玉溪师专学报：综合版，1998， 14 （6） ： 43.

[7]席高文，许梦日.中学几何研究与教学[M] . 郑州：郑州大学出版社，2007： 174.

作者单位

（广东省佛山市南海区桂城街道映月中学;广东;佛山;528000）