基于薛定谔方程的光纤传输过程

于 涧, 刘 玲, 连俊芳

(1.沈阳师范大学 数学与系统科学学院, 沈阳 110034; 2.北华航天工业学院 文理学院, 河北 廊坊 065000; 3.怀仁十一中, 山西 怀仁 038399)

0 引 言

非线性偏微分方程[1]作为数学模型在很多领域中都起着重要作用。作为描述波包在非线性介质中传播的方程-非线性薛定谔方程,在非线性物理方程学中具有重要地位。光纤几乎都是非均匀的,在实际应用中其损耗一般是不能达到理想化的,于是采用非线性薛定谔方程[2]描述其对应的传输过程。上述方程已具有其对应解法,如相似变换法[3]、Hirota方法[4]等。又因为光脉冲传播较为复杂,且长距离传播和其他客观原因所引起的损耗是不能忽视的, 于是建立变系数耦合非线性薛定谔方程[5]模型。高维耦合非线性薛定谔方程[6-9]的解可以解释相对较丰富的物理现象。所以将(1+1)-变系数耦合非线性薛定谔方程拓展到(2+1)-维变系数耦合非线性方程。

1 孤子解

应用(2+1)-维变系数耦合非线性薛定谔系统描述带有偏振效应的二维渐变折射率非线性波导放大器内一束光的传输过程:

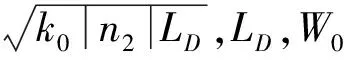
构造变换:

这里的g和h是关于x,y,t的复函数,f是实函数。

其中Dx,Dy和Dz是双线性算子,f(x,y,t)是变量x,y与t的可微函数。

当μ(t)=β(t)γ2(t)-γ′(t),令χ(t)=aβ(t),a为常数,方程(3)和方程(4)的双线性形式如下所示:

基于式(5)和式(6),方程组(1)和方程组(2)的孤子解可由以下展开式得到:

式中:ε是参量;gi和hi(i=1,3,5,…)是x,y和t的复函数;fj(j=2,4,6,…)是x,y和t的实函数。把式(7)和式(8)代入双线性形式(5)和式(6)中,令ε的同幂次项系数为零,当N=1时,式(5)和式(6)可截断至

g=εg1=εAeθ,h=εh1=εBeθ,f=1+ε2f2=1+ε2Ceθ+θ*,

可以得到

当N=1时,取ε=1,从而可得(2+1)-维变系数耦合非线性薛定谔方程(1)和方程(2)的单孤子解为

2 孤子的传输特性

2.1 畸形波

根据(2+1)-维变系数耦合非线性薛定谔方程(1)和方程(2)的解(12)、(13),选取如下所示参量得到畸形波[14-15]解。

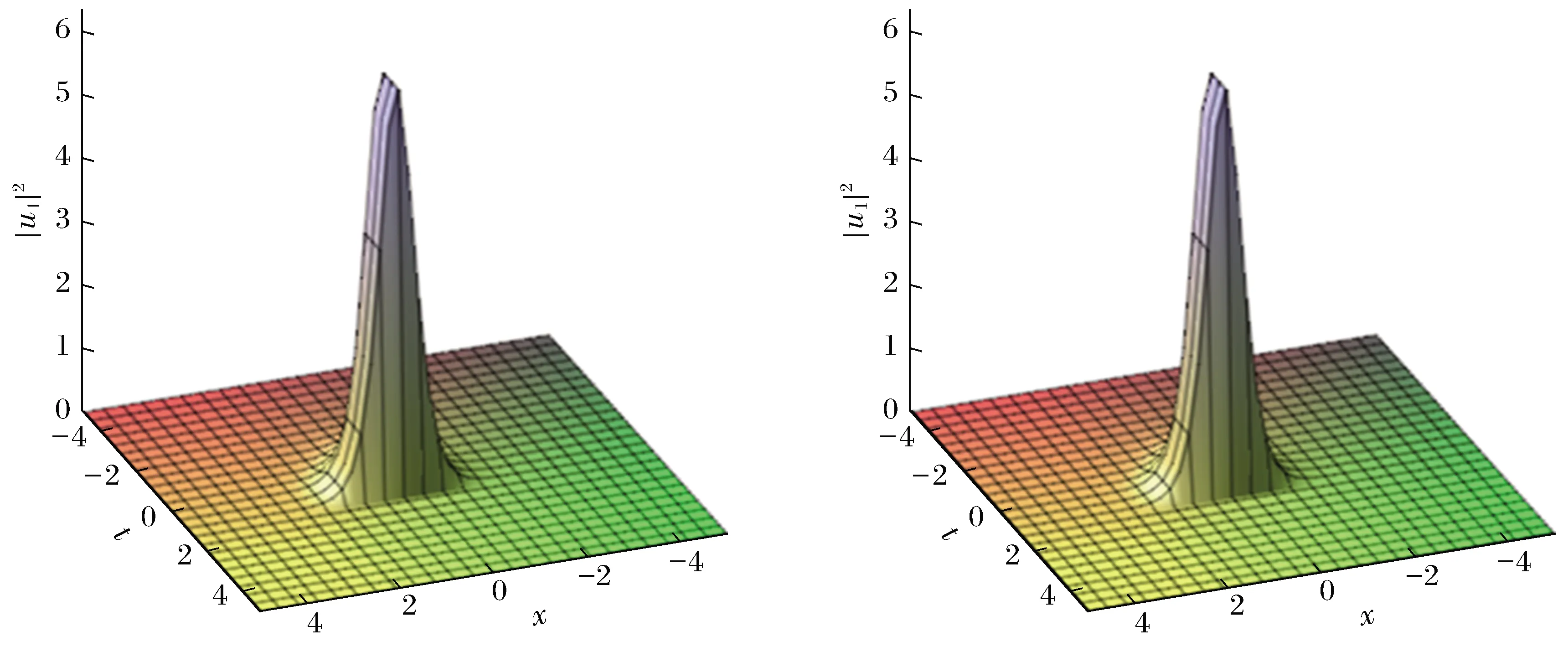
图1 畸形波解u1的演化图像(y=0;x=0)

2.2 单孤子的传输特性

图2显示了当k1=1,k2=2,A=B=1且β(t)=χ(t)=1时γ(t)=0,即衍射效应和非线性效应都为常数,增益(损耗)系数为零,在x-t,y-t平面上单孤子以亮孤子的形式传输,且方向、宽度和振幅均保持不变,孤子可以稳定的传输信息。

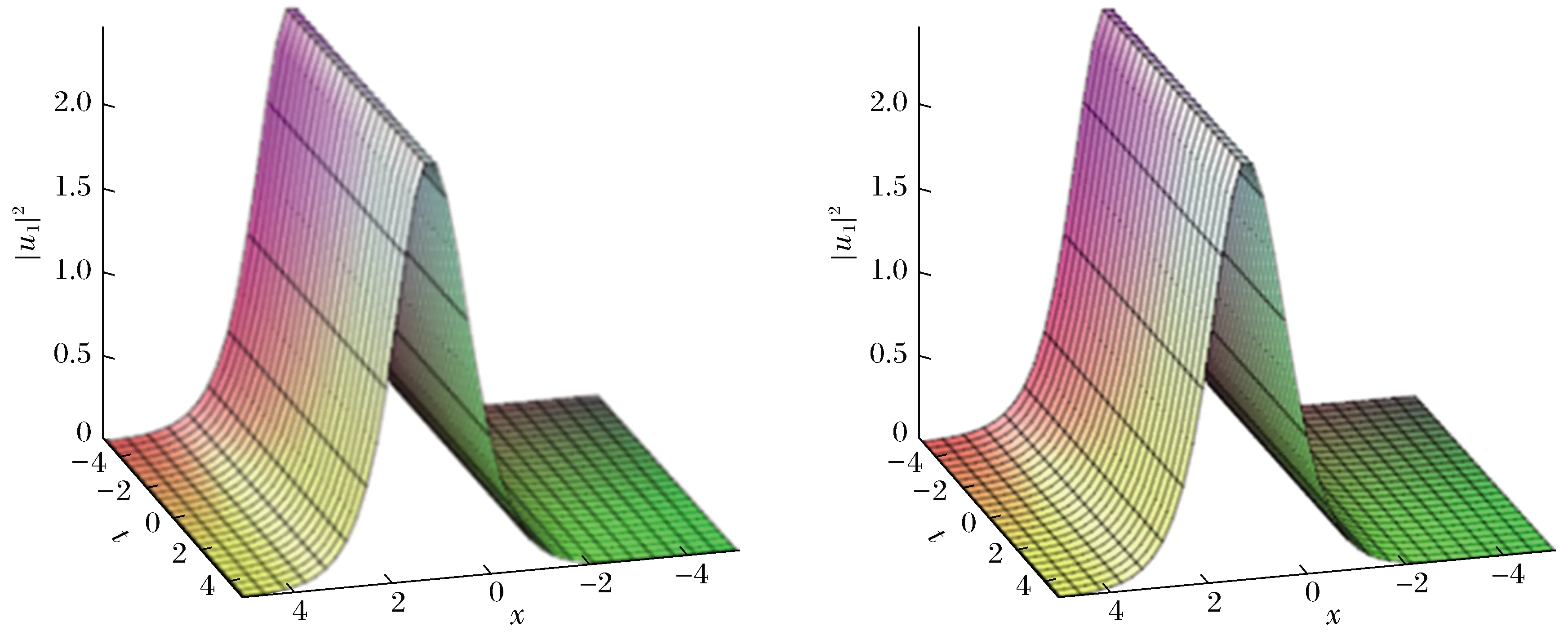
图2 单孤子解u1的演化图像(y=0;x=0)

3 总结与展望

基于一类薛定谔方程的孤子解和畸形波解定量分析传输特性和衍射效应等因素在光束传输过程中对光纤传输的影响,并列举了不同参数下畸形波解和孤子解的演化过程。根据上述对比,结合实际需求可选取合适的参数使损耗降到最小。