区间直觉模糊集下TOPSIS招聘模型

张燕丽, 占玉芬, 黄淑伟

(沈阳师范大学 软件学院, 沈阳 110034)

0 引 言

近年来,越来越多的研究人员正在关注基于直觉模糊集(Intuitionistic Fuzzy Set, IFS)[1]和直觉区间模糊集(Interval-Valued Intuitionistic Fuzzy Set, IVIFS)[2]的聚合,IVIFS不仅包含隶属度信息,还考虑了非隶属度和犹豫度信息,一些学者利用IVIFS理论解决多属性决策问题[3-5],并在处理不精确信息[6]方面取得了较好的效果。为了度量目标的不确定性信息,本文将IVISF理论应用于校园招聘,评估和选拔毕业生,确定最终人选。该方法有效地处理招聘活动中的不确定、不完整的信息,使招聘流程更加公平。有许多基于IFS和IVIFS的聚合方式,其中,通过逼近理想点的排序方法(The Technique for Order Performance by Similarity to Ideal Solution, TOPSIS)最早是由Hwang和Yoon[7]所发展出来的一种多属性决策方法。对于一个决策优化问题,如果各个方案的属性值都能达到最优,并且对于决策的目标结果也能达到最优,这就是“正理想点”。反之,各属性值最差并且决策目标值最小,即为“负理想点”[8-9]。实际问题中,正负理想点都是小概率存在的,所以对于每个方案,判断每个方案与正负理想点的接近情况,综合考虑所有备选方案信息,进行最终排序[10]。

校园招聘效能测评指标体系的构建[11],主要从学生个人获得的荣誉及在思想道德、社会实践、技能训练、学业成绩、创新、体能素质、学习态度、志愿服务、心理素质、个性特长等方面[12],根据专家意见可归纳为专业能力、活动能力、基本素养以及创新能力4个方面评估学生的个人能力。通过建立评估指标实现公平就业,多属性决策可以有效解决企业校园招聘过程中的公平问题,在这个决策问题中,有不同的学生作为备选方案,还有一组招聘人员作为决策者,通常需要他们提供关于备选方案在各指标偏好值。为了综合决策小组对备选方案的意见,需要聚合所有属性信息。

因此,本文通过计算IVIFS中逼近理想点法,同时考虑区间直觉模糊集的精确程度,将其与正负理想点聚合,提出一种解决多属性决策问题的TOPSIS方法。本文结构如下:第1部分介绍IVIFS和IVIFS的精确函数,结合IVIFS的犹豫度改进IVIFS的精确函数。第2部分描述基于IVIFS的TOPSIS的步骤,并在第3部分以具体的校园招聘实例表明算法的合理性,第4部分总结文章。

1 预备知识

1.1 直觉区间模糊集(IVIFS)

1.2 区间直觉模糊集的得分函数和精确函数

得分函数值越大,区间直觉模糊数对应的方案越优,在得分函数相等情况下精确函数越大则对应的方案越优。但是上述的函数没有考虑到犹豫度对决策结果的影响,有一定的局限性。例如,以下有两组区间直觉模糊值。A1=[0.4,0.5],[0.3,0.4];A2=[0.4,0.5],[0.2,0.5]。用公式(1)和(2)计算得分函数和精确度结果为:S(A1)=S(A2)=0.1;H(A1)=H(A2)=0.8。从结果不能区分A1和A2的优劣,为此对函数进行改进,以精确函数为主,考虑犹豫度的影响,改进后的公式如(3)所示[14]。

(3)

公式(3)计算A1和A2精确度为H(A1)=0.545,H(A2)=0.550。表明A2优于A1,A1犹豫度更高。改进后的精确函数在计算时考虑了犹豫度信息对决策的影响,使得决策结果更准确[15]。

1.3 TOPSIS评估法

TOPSIS法是根据有限个评估对象与理想化目标的接近程度进行排序的方法,是在待评估的对象中进行相对优劣的评价方法。排序规则是把各备选对象与正负理想解作比较,其中接近正理想解,而同时又远离负理想解,则该对象是最好的备选方案。TOPSIS评估方法首先构造具有评估对象和指标的决策矩阵,确定出正理想解和负理想解,计算各个评估对象与正理想解之间的距离,以及各个评估对象与负理想解之间的距离,最后计算每个评估对象之间的相对接近度[16]。

2 基于IVIFS和TOPSIS方法的决策模型

步骤1 标准化决策矩阵。指标分成2类:效益指标、成本指标,为了平衡这些评价指标的物理维度,将决策矩阵D=[αmn]i×j通过下列公式标准化后转变成矩阵R=[rmn]i×j,对于效益型指标采用公式(4),对于成本型指标通过公式(5)转化。

(4)

(5)

步骤2 确定备选方案的正负理想点。据标准化后矩阵R,通过公式(6)、式(7)确定备选方案的正理想点(PIS)和负理想点(NIS)。

(6)

(7)

步骤3 确定各备选方案接近PIS程度以及远离NIS程度。依据公式(8),同时考虑各指标下区间直觉模糊集的精确程度,定义衡量精确度的公式(9),hmn越大表明精确程度越高。amn代表接近PIS或者远离NIS的程度,cmn代表远离PIS和接近NIS的程度。

(8)

(9)

(10)

(11)

步骤4 聚合备选方案权重值。集合在属性权重下各备选方案组成的与理想点接近或远离程度,备选方案和PIS之间整体的同一程度以及备选方案和NIS之间的对立程度,定义公式如下:

步骤5 计算各备选方案的相对接近系数,并根据Τ(Am)降序排列各个备选方案。

(14)

3 实例分析

经过筛选,3位学生符合招聘条件,用Ai(i=1,2,3)表示。招聘主管将评估学生能力的指标分为四个,用Gj(j=1,2,3,4)表示。其中G1:专业能力、G2:活动能力、G3:基本素养、G4:创新能力。ω=(0.4,0.2,0.3,0.1)为对应权重。表1是负责招聘人员以区间直觉模糊值的形式给出评价。

表1 IVIFS决策矩阵

依据公式(4)标准化决策矩阵,结果如表2所示。

表2 标准化后的IVIFS决策矩阵

根据标准化后的数值,用公式(6)、(7)评定出PIS和NIS结果如下:

依据公式(8)计算3个学生接近PIS程度或远离NIS程度,计算精确度采用公式(9),同时将IVIFS精确度考虑到正负理想点的程度利用公式(10)和(11)计算,结果如表3所示。

表3 备选方案与正负理想点接近或远离程度

利用式(12)、式(13)计算与正负理想点接近或远离程度的权重聚合,结果如表4所示。

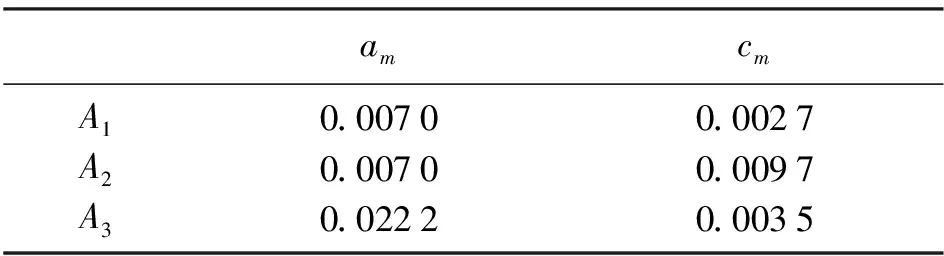
表4 权重值聚合的结果

公式(14)计算结果为T(A1)=0.724,T(A2)=0.418 0,T(A3)=0.863,降序排列3个学生的总体表现排名A3、A1、A2。

4 结 语

本文的目的是提出一个基于IVIFS的逼近理想解方法,用于解决区间直觉模糊集环境下校园招聘的多属性决策问题。在决策过程中,基于数据计算正负理想方案,构造出各个备选方案与正负理想点的接近或远离程度,最重要的是考虑了区间直觉模糊集的精确度,并将其与正负理想点的接近或远离程度聚合。在此基础上,结合各个指标的权重值,确定各备选方案的加权数,根据计算出与正负理想点的接近或远离程度进行排序。本文通过校园招聘实例验证了该方法的合理性、有效性。