圆盘约束下抵御传感器故障的静态输出可靠控制

姚 波, 叶倩玉, 武全胜, 王福忠, 何 新

(1.沈阳师范大学 数学与系统科学学院, 沈阳 110034;2.朝阳师范高等专科学校 数学计算机系, 辽宁 朝阳 122000; 3.沈阳工程学院 基础部, 沈阳 110036)

随着现代工业系统对安全性和可靠性需求的不断增加,尤其是飞机、航天器和核电站等系统。线性系统的稳定性分析和可靠控制器设计的综合问题吸引了越来越多的研究者的关注[1-4]。在实际系统中,由于传感器或执行器的老化和电磁干扰等问题,故障经常会发生,可能会导致系统性能无法承受[5]。因此,引入了可靠控制方法[6-8]来应对执行器和传感器的故障,并进一步保持系统的稳定性和性能指标。传感器容易发生故障,而且与执行器相比,传感器故障可能会导致更严重的情况。因此,为了提高系统的可靠性和安全性,已开发出各种可靠的控制技术,以补偿传感器故障并保持闭环系统的性能。文献[9]针对不确定线性系统执行器出现混合故障的模型,通过求解线性矩阵不等式完成状态反馈可靠控制器的设计。然而状态反馈控制器在实际控制工程中,往往不能直接观测得到,对系统进行控制是难以实现的。那么,考虑输出反馈对系统进行控制,其中动态输出反馈控制器有消耗资源过大的弊端[10],所以静态输出反馈控制器是一种基于控制理论的有效控制策略,被广泛应用于飞行器和工业控制过程中[11-12]。这一方法的好处在于可直接测量获得数据,但所得到的结论难于求解。此外,系统的瞬态性能对于实际工程中也是至关重要的,主要取决于系统极点的位置。将系统的极点分配到某些特定区域,则可以获得相应的良好瞬态性能[13-15]。

本文利用凸组合方法处理故障[16],通过数学方法把结论转化为线性矩阵不等式(LMI)形式,应用MATLAB中LMI工具箱求解线性矩阵不等式,获得可行解。将极点约束在特定的圆盘区域内,以获得相应的良好瞬态性能。无论是否发生传感器单故障,系统的极点均配置在特定的圆盘区域内且保持渐近稳定。

1 问题描述

考虑线性定常系统:

(1)

其中:x(t)∈Rn为系统的状态变量;y(t)∈Rm为系统的测量输出变量;u(t)∈Rp为系统的控制输入变量;A,C为适维矩阵;B为适维列满秩矩阵。

传感器连续增益单故障矩阵模型为yf(t)=Fsy(t)。其中y(t)∈Rm为传感器正常信号向量,yf(t)∈Rm为考虑传感器单故障的信号向量,Fs为传感器单故障矩阵,其形式为

其中,fsi为第i条传感器通道上的增益值,且满足

考虑传感器故障的信号向量yf(t)就可以表示为

yf(t)=[y1(t),…,yi-1(t),fsiyi(t),yi+1(t),…,ym(t)]T

这种故障形式称为任意单一故障。任意单一故障具有如下2个特点:1)在m个传感器中,任意一个传感器都可能出现故障;2)最多只有一个传感器出现故障。

故障处理(凸组合法)

考虑传感器单故障,设

设集合

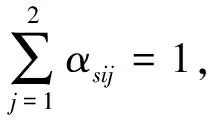
以上描述的传感器单故障矩阵集合可以推广到任意传感器多故障矩阵集合中,因此在实际应用中,传感器部件从单一故障到多故障均可采用此方法设计的控制器进行可靠控制,并且大大减小了只从多故障角度设计控制器的保守性。

引理1 已知S是n×n正定矩阵,B是n×m列满秩矩阵(m≤n),则矩阵BTSB可逆。

证明 利用反证法,及S是n×n正定矩阵,可得BTBX=0有非零解;又因B是列满秩矩阵,所以BTBX=0只有零解,矛盾。所以BTSB可逆。

2 主要结论

2.1 基于圆盘约束的线性系统静态输出反馈控制器设计

对线性系统(1)引入静态输出反馈控制器:

u(t)=Ky(t)

(2)

由此得到闭环系统:

(3)

定理1 对于闭环系统(3),存在静态输出反馈控制器(2),使所有特征值均在半径为r,圆心为(-q,0),(r>0,q>0)的圆盘中的充分必要条件是对于正定矩阵P和矩阵U,W使得下列线性矩阵不等式组(LMI):

(4)

存在可行解。如果可行解为(P,U),则相应的静态输出反馈控制器增益矩阵K=W-1U。

其中,W可以由PB=BW求得。

证明 由引理2可知,存在正定矩阵P使闭环系统(3)的极点配置在指定的圆盘区域内,令PB=BW,WK=U,可得式(4)。

下证W可逆:

由B为列满秩矩阵,对等式PB=BW两边左乘以BT得BTPB=BTBW,则W=(BTB)-1BTPB,即BTPB可逆,由引理1可知BTPB可逆,故W可逆。

综上,定理得证。

2.2 基于圆盘约束的线性系统传感器故障的静态输出反馈可靠控制器设计

当线性系统发生传感器故障,系统可以描述为

(5)

对系统(5)引入静态输出反馈控制器:

u(t)=Kyf=KFsy(t)=KFsCx(t)

(6)

由此得到闭环系统:

(7)

定理2 对于闭环系统(7),存在静态输出反馈可靠控制器(6),使所有特征值均在半径为r,圆心为(-q,0),(r>0,q>0)的圆盘中的充分必要条件是对于正定矩阵P和矩阵U,W使得下列线性矩阵不等式组(LMIs):

(8)

i=1,2,…,m;j=1,2

存在可行解。如果可行解为(P,U),则相应的静态输出反馈控制器矩阵增益K=W-1U,其中W可以由PB=BW求得。

证明 由引理2可知,存在正定矩阵P使闭环系统(7)的极点配置在指定的圆盘区域内必须满足

即

令PB=BW,WK=U,得

(9)

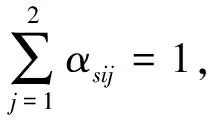
故有

W可逆的证法与定理1相同(故省略)。综上,定理得证。

3 数值仿真

考虑系统:

易知开环系统极点为λ={0.732 1 -2.000 0 -2.732 1},因此系统不稳定,其中极点0.732 1不在半径为r=3.6,中心为(-3.6,0)的圆盘中。

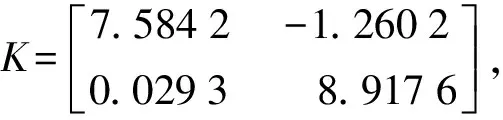
图1 极点配置在圆盘区域内

再考虑传感器发生单故障情况F=diag(fs1,fs2),其中0.1≤fs1≤2.4,0.2≤fs2≤1.4,在原有的反馈控制器的作用下,闭环系统的部分极点跳出特定圆盘区域,如图2所示。

图2 系统发生传感器故障,部分极点跳出圆盘区域

图3 带有可靠控制器的系统,全部极点落在圆盘区域

4 结 论

针对线性系统,研究了具有传感器连续增益单故障的情况下,采用线性矩阵不等式(LMI)处理方法,利用连续故障模型凸组合方法,给出了闭环系统在圆盘约束下的可靠控制器的设计。数值仿真将传感器各通道可能发生的故障情况均展现出来,静态输出反馈可靠器均能保证系统的极点在圆盘约束内且系统保持渐近稳定,保证了工程领域的高精度要求。