熔融耦合器中耦合模式与新型孤子结构*
2022-12-14李森清张肖林机
李森清 张肖 林机
(浙江师范大学物理系,金华 321004)
研究了非局域非线性熔融耦合器的耦合模式构建新型孤子结构和稳定性的关联性.对于高斯型耦合模式,存在多极类亮孤子、平顶孤子和多极灰孤子结构.一至三极对称峰值的类亮孤子、灰孤子和平顶孤子传播是稳定的,孤子峰值不同的三极类亮孤子和三极灰孤子均不能稳定.研究发现灰度将影响灰孤子传播的稳定性.通过调制耦合函数宽度,可实现孤子结构的转换.
1 引言
自从Snyder 和Mitchell[1]提出强非局域非线性介质中光孤子以后,非局域介质中的空间光孤子性质的研究引起了科学研究者的广泛兴趣,发现介质的非局域性具有抑制平面波的调制不稳定性、防止复杂光束的灾难性坍塌以及稳定复杂结构的孤子等作用,在非局域介质中可以实现许多复杂的空间光学孤子结构,如正弦高斯孤子[2,3]、涡旋孤子[4]、螺旋椭圆孤子[5]、多极孤子[6−8]、表面波孤子[9]、呼吸子[10,11]、环暗孤子以及类亮孤子[12]等丰富的孤子结构.
光学耦合器是通信系统中重要的节点器件之一,是一种用于实现光信号放大、转换和调制等功能的装置,可用作功率分路器或合路器[13]、波分复用器[14]、滤波器[15]、非线性全光开关[16]等.1976 年,Barnoski 和Friedrich[17]利用二氧化碳激光器加热和熔融两根光纤,成功制造出第一个光纤定向耦合器.此类的耦合器可以通过调节光纤纤芯间距和熔融段相互作用长度来控制耦合比.加热和熔融方法为耦合器的大规模生产提供了相当大的技术支持.由于具有一些特殊性质及潜在的应用,熔融耦合器引起了许多光学学者的研究兴趣[18−21].大多数的熔融耦合器是耦合强度不变的耦合器[22,23].同时也存在耦合器形状变化导致芯间介质不均匀分布的变耦合强度的耦合器,如波长滤波器的波导耦合器的信道之间耦合是随传输距离的可变函数[24,25],它可以控制光束的传输过程.另一种是耦合强度随横向位置会发生变化的熔融耦合器,依赖关系可以用一些函数来近似,如δ函数[26]、高斯函数[27]、余弦函数[28].
在具有非局域非线性效应的熔融耦合器中可以传输稳定的空间孤子.Shi 等[29]基于斯奈德-米切尔模型提出了非局域非线性耦合器模型,采用变分法预测孤子对称破缺的临界值功率和孤子稳定性分界的临界值功率,并讨论孤子的控制、开关和分裂问题;Mandal 和Chowdhury[30]研究了光孤子在熔融耦合器中传播的拉曼散射和开关效应,得出了在耦合器的一个臂上发射光孤子可以在两个臂上产生光孤子,但当拉曼散射的强度发生变化时光孤子模式显著不同的重要结论;文献[31]设计了一种产生暗孤子的方案,即由熔融耦合器中一个臂上的亮孤子与另一个臂的长脉冲相互作用而产生,还提出一种计算暗孤子参数的解析方法.我们利用对称约化方法和数值计算方法研究了非局域熔融耦合器中孤子结构,得到偶极孤子、双峰孤子、多极亮暗孤子、周期孤子、准周期孤子和类Airy 解等丰富孤子解[32,33],并给出多极孤子的稳定性.然而通过调控熔融耦合器中耦合模式实现不同孤子结构的报道很少,且熔融耦合器中不同的耦合模式会导致不同的孤子结构;同时熔融耦合器中存在的孤子态,其稳定性和传输特性对于光学器件的性能和信息的有效传递起着关键性作用,因此本文主要研究非局域非线性熔融耦合器中的一些新型孤子结构及动力学行为.
2 熔融耦合器中新型空间孤子
2.1 理论模型
光束在非局域非线性熔融双芯平面波导耦合器中传播可用变耦合强度的非线性薛定谔方程描述:

其中Wj为孤子的振幅,b为孤子的传播常数;利用牛顿迭代方法对方程(3)和(4)求解,获得类亮孤子、平顶孤子以及灰孤子解.Harel 和Malomed[26]介绍耦合强度为δ函数,给出了一个或几个短片段上局域耦合双芯波导耦合器中孤子的动力学行为;文献[33]的作者获得了耦合强度为高斯函数的非局域非线性熔融双芯平面波导中孤子解及其稳定性.受文献[26]和文献[33]研究结果的启发,本文理论上设计了耦合模式存在不同的函数形式,试图从数值上探索更丰富稳定的孤子结构.
2.2 基态类亮孤子
利用牛顿迭代方法求解方程(3)和方程(4).ρj(x)=αjexp(-x2/ω),其中ω是耦合函数宽度,αj为耦合强度振幅.当α1=15 ,α2=9,ω=0.01 时,可得到图1 所示的基态类亮孤子解.图1(a)表明基态类亮孤子的孤子峰值和束宽随非局域程度d的增大而增大.由于非局域程度的增大,介质的非线性效应减弱,而光束的衍射效应增强,导致孤子的宽度增大.m1和m2的值在熔融双芯耦合器的中心位置x=0 处相差最大,导致光束幅值U1和U2相差最大.在图1(b)中,改变传播常数b,发现随着传播常数b减小,类亮孤子的峰值是增大的.当x→∞时,类亮孤子和暗孤子一样有渐近行为,即=-b,mj(x→∞)=b.折射率随着传播常数b的减小而减小,并且折射率呈两侧升起的反钟形分布,当折射率达到最小值时,孤子峰值达到最大值,并且随着传播常数b的减小,基态类亮孤子两边的凹陷越来越明显.在图1(c)中,基态类亮孤子的束宽和峰值随着非线性参数β2减小而减小,而折射率mj的波形分布因非线性参数βj的变化存在一定的差异.当β1固定时,m1随着β2的减少而增大,而m2随着β2的减少而减小.类似地,当β2固定时,m2随着β1的减少而增大,而m1则随着β1的减少而减少.同时β1和β2相差越大,两分量的孤子峰值以及对应的折射率m1和m2相差越大.从图1(d)和图1(e)得知,孤子功率是随着ω增加而增加的,并且ω<0.2 的范围内功率增加得最快.ω→1时,功率趋于常量.加上5%随机白噪声的解作为初始扰动解,用龙格库塔方法模拟该扰动解的演化,发现基态类亮孤子能稳定地长距离传输.

图1 基态类亮孤子波形和功率图 (a) β1=β2=-1,b=-0.4,d 分别为0.2,3.0 和7.0 时对应的波形;(b) β1=β2=-1,d=0.2,b 分别为–1.0,–2.5 和–5.0 时对应的波形;(c) b=-0.4,d=0.2,β1=-1,不同 β2 对应的波形(β2=–2,–4 和–8);(d)当 β1=β2=-1,d=0.5 时,不同传播常数情况下,功率与耦合函数宽度的关系;(e)当 β1=β2=-1,b=-0.5 时,不同非局域程度情况下,功率与耦合函数宽度的关系Fig.1.Waveform and power diagram of ground state bright-like soliton: (a) Corresponding waveform of β1=β2=-1,b=-0.4,d selected as 0.2,3.0 and 7.0,respectively;(b) corresponding waveform of β1=β2=-1 ,d=0.2,b selected as–1.0,–2.5 and–5.0,respectively;(c) waveform corresponds to different β2 when b=–0.4,d=0.2,β1=-1 (β2 selected as–2,–4 and–8,respectively);(d) when β1=β2=-1,d=0.5,the relationship between the power and coupling function width under different propagation constant;(e) when β1=β2=-1 ,b=-0.5,the relation between the power and coupling function width under different nonlocal degree.
2.3 多极类亮孤子及其稳定性
通过改变试探解、耦合模式以及选择合适参数可以得到多极类亮孤子.当耦合模式为两个高斯组合时(ρj(x)=αj{exp[-(x+H)2/ω]+exp[-(x-H)2/ω]},H为耦合强度最大值位置),可以得到两极类亮孤子.耦合强度最强的位置分别处于x=-H和x=H左右,对应的类亮孤子峰值达到最大值,此时折射率为最小值.图2(a)展示了不同耦合宽度下的两极类亮孤子.即当ω→0 且小于0.1 时,两极类亮孤子的峰值和束宽减小,而两极孤子间的距离增大.当ω>0.1 时,两极类亮孤子的峰值和束宽增大,两极孤子间的距离减小,因此可以通过调节耦合函数宽度来控制孤子的峰值、束宽以及孤子间的距离.当ω=0.1 时,增加非局域程度,两极类亮孤子的孤子峰值和束宽是增加的,但是在两极类亮孤子的两端出现了凹陷,如图2(b)所示,这跟基态类亮孤子随着传播常数的减少而孤子两端出现凹陷的情况类似.非局域程度d越大,凹陷的程度越明显,对应的折射率形成较高的折射率分布,变成一个平缓的波谷.为了证实两极类亮孤子解的稳定性,当d=2,两极类亮孤子在微扰的情况下依然可以保持稳定传输,如图2(c)所示.改变H,可以改变孤子间的距离.即增大H的值可以得到图2(d)的孤子分子,这样的孤子分子在微扰的情况下也能稳定传输.因此可以通过改变耦合强度最大值位置H来决定孤子间的距离,从而输出所需要的光孤子信号.
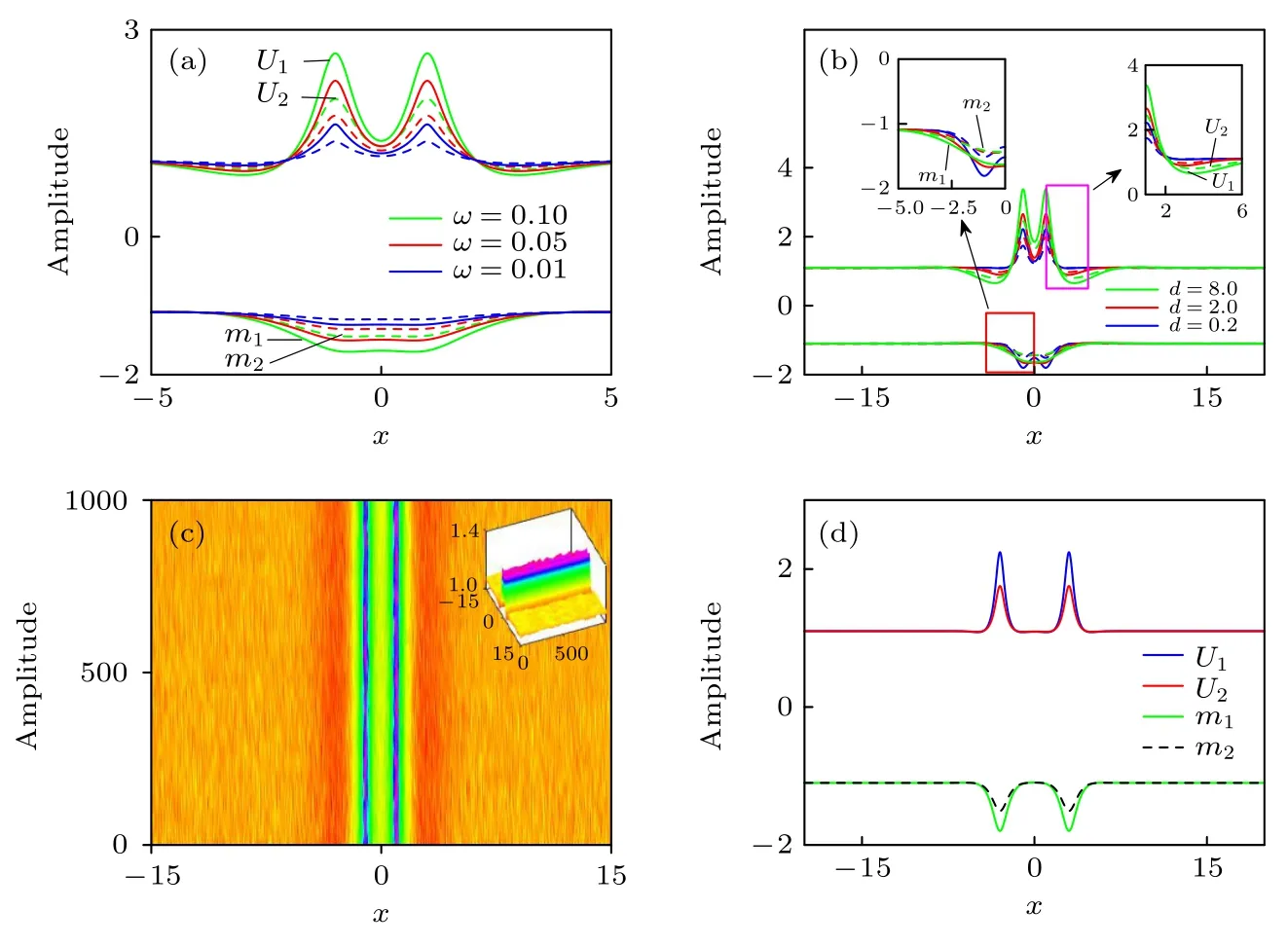
图2 两极类亮孤子的强度分布和传输特性 (a)当 d=0.2,H=1,ω 分别为 0.1,0.05 ,0.01 时,两极类亮孤子的强度分布图;(b)当 b=-1.1,ω=0.1,H=1,d 分别为 0.2,2,8 时,两极类亮孤子的强度分布图;(c)对应图(b)中 d=2 时,U1 的加噪传输图;(d) d=0.2,b=-1.1,ω=0.1,H=3 时,孤子分子的强度分布图Fig.2.Intensity distribution and propagation properties of bipolar bright-like solitons: (a) When d=0.2,H=1,ω is 0.1,0.05,0.01,respectively,intensity distribution of bipolar bright-like solitons;(b) when b=-1.1,H=1,ω=0.1,d is 0.2,2,8,respectively,intensity distribution of bipolar bright-like solitons when the degree of nonlocality;(c) corresponding to the white noise propagation graph of U1 when d=2 in panel (b);(d) intensity distribution of soliton molecule when d=0.2,b=-1.1,ω=0.1,H=3.
当β1=β2=-1,b=-1.1,α1=2,α2=1,ω=0.1,d=0.2,H=2,ρj(x)=αj{2 exp[-(x+H)2/ω]+exp(-x2/ω)}时,得到图3(a)的非对称峰值的两极类亮孤子,孤子的波形与折射率波形类似.在5%的微扰情况下,这样的两极类亮孤子能够长距离稳定传输.同样改变H的大小可以控制两极孤子间的距离,得到非对称峰值的孤子分子.当耦合器中双芯的耦合模式不同时,得到模式不同的非对称峰值的两极类亮孤子.当

时获得图3(d)所示的非对称峰值的两极类亮孤子.由于图3(d)折射率相对图3(a)有所增大,使得孤子之间的吸引相互作用增强,且各自孤子峰值大小都有所减小,这样的两极类亮孤子不能稳定地传输(见图3(e)).经过大量的数值计算发现,当两分量的孤子模式不相同时,孤子就会出现不稳定传输.为了进一步证实孤子解的稳定性,对其进行线性稳定性分析,得到线性扰动增长率实部与虚部图(见图3(c)和图3(f)),这里把稳定性问题的求解转化为本征方程的本征值λ问题.不稳定性来源于λ存在实部的正数,即扰动随着λ实部的正数k=Re(λmax)指数增长,从而导致孤子模式不同时出现不稳定传输,如图3(f)所示,同样证实了图3(d)中解的不稳定.

图3 非对称峰值的两极类亮孤子的强度分布和传输特性 (a)耦合模式相同时,非对称峰值的两极类亮孤子的强度分布图;(b) 图(a)孤子解 U2 的加噪传输图;(c) 图(a)孤子解的稳定性图谱;(d)耦合模式不同时,非对称峰值两极类亮孤子的强度分布图;(e)图(d)孤子解 U1 的加噪传输图;(f)图(d)孤子解的稳定性图谱Fig.3.Intensity distribution and propagation properties of bipolar bright-like solitons with asymmetric peaks: (a) Intensity profiles of bipolar bright-like solitons with asymmetric peaks with the same coupling mode;(b) propagation of soliton solution U1 with the white noise in panel (a);(c) stability spectra of soliton solutions in panel (a);(d) intensity distribution of bipolar bright-like soliton with different patterns of asymmetric peaks with different coupling modes;(e) propagation of soliton solution U1 with the white noise in panel (d);(f) stability spectra of soliton solutions in panel (d).
类似于两极类亮孤子情形,选取

得到图4(a)所示的三极类亮孤子.三极类亮孤子的波形和折射率波形类似两极类亮孤子,只是折射率中心区域向下凹陷的波谷数与三极类亮孤子的极数相同,呈向下的钟形轮廓,并且孤子峰值越小的三极类亮孤子,折射率分布在x=0 点附近有小小的波形调制.孤子峰值对应的折射率最小,导致较大的排斥.而两孤子交界处对应形成局部足够高的折射率分布,引起两孤子的相互吸引,当排斥相互作用最终被吸引相互作用平衡,就会形成三极类亮孤子束缚态.图4(b)中的三极类亮孤子加上随机扰动也能像两极类亮孤子一样稳定传输.当H增大时,也可得到传输稳定的孤子分子.当耦合模式为ρj(x)=αjexp(-x2/ω),β1=-1,β2=-2,α1=15,α2=9,ω=0.8 时,得到图4(c)所示模式相同的三极类亮孤子,但是孤子峰值不同,随着演化距离的增加,三极类亮孤子先逐渐变成两极类亮孤子,再变成单极类亮孤子,最终出现发散,如图4(d)所示.当β1=β2=-1,b=-1.1,d=0.2,α1=2,α2=1,ω=0.1,

时得到如图4(e)所示的耦合模式不同的三极类亮孤子.发现它们的传输与耦合模式不同的两极类亮孤子一样,也不能稳定传输,如图4(f)所示.进一步发现,非对称峰值的三极类亮孤子不能像非对称峰值的两极类亮孤子一样长距离稳定传输.

图4 不同类型的三极类亮孤子的强度分布和传输特性 (a) β1=β2=-1,b=-1.1,d=0.2,α1=2 ,α2=1,H=1,ω=0.1 时,三极类亮孤子的强度分布图;(b) 图(a)孤子解 U1 的加噪传输图;(c) β1=-1,β2=-2,α1=15 ,α2=9 ,ω=0.8,d=1.5,b=-0.5 时,孤子峰值不同的三极类亮孤子的强度分布图;(d) 图(c)孤子解 U1 的加噪传输图;(e)耦合模式不同时,非对称峰值三极类亮孤子的强度分布图;(f) 图(e)孤子解 U2 的加噪传输图Fig.4.Intensity distribution and propagation characteristics of three-pole bright-like solitons with different types: (a) Intensity distribution of three-pole bright-like solitons when β1=β2=-1,b=-1.1,d=0.2,α1=2,α2=1,H=1,ω=0.1 ;(b) propagation diagram of soliton solution U1 with the white noise in panel (a);(c) intensity distribution of three-pole bright-like solitons with different soliton peaks when β1=-1,β2=-2,α1=15,α2=9,ω=0.8,d=1.5,b=-0.5 ;(d) propagation diagram of soliton solution U2 with the white noise in panel (c);(e) intensity distribution of the asymmetric peak three-pole bright-like solitons with different coupling modes;(f) propagation diagram of soliton solution U2 with the white noise in panel (e).
2.4 平顶孤子和灰孤子
文献[34]中,利用牛顿迭代法得到了常耦合强度的非局域非线性薛定谔方程的暗孤子解.方程(1)和(2)也可以得到稳定传输的暗孤子解.除此之外,变耦合强度的非局域非线性薛定谔方程可以得到更为丰富的孤子结构,如平顶孤子解和灰孤子解.当ρj(x)=αjexp(-x2/ω),β1=-1,β2=-2,α1=15,α2=9,ω=0.8,d=1,b=-0.5 时,得到图5(a)所示的平顶孤子,并且在微扰的情况下可以稳定传输(见图5(b)).当非局域程度d=1 时,改变ω,发现在 0.1<ω≤0.86 时存在平顶孤子.当0.05<ω≤0.09 时,平顶孤子变成暗孤子;当ω≤0.05 时,暗孤子变成灰孤子,ω→0 时,灰孤子的灰度变小.当ω=0.05时,得到图5(c)所示的单极灰孤子.当非局域程度d≥2 时,单极灰孤子不能稳定地传输.减小ω,单极灰孤子的灰度变小且光束的宽度变窄.发现灰孤子的灰度越小越难稳定传输.如同暗孤子是处于基态的孤子,容易稳定传输,而灰孤子是处于激发态的孤子不容易稳定传输.灰孤子的灰度越小,处于更高的激发态上,就更难稳定传输.当ρj(x)=αj{exp[-(x+H)2/ω]+exp[-(x-H)2/ω]},β1=β2=-1,b=-0.4,d=0.2,α1=11,α2=10,ω=0.05,H=2 时,得到两极灰孤子(见图5(e)).增大H的值得到长距离稳定传输的孤子分子.经数值计算发现,在合适的参数下,单极灰孤子和两极灰孤子在白噪声条件下依然可以长距离地传输,如图5(d)和图5(f)所示.同样对灰孤子解进行线性稳定性分析,得到λ只存在虚部,也证实了其解的稳定性.

图5 平顶孤子、单极灰孤子、两极灰孤子的强度分布和传输特性 (a)当 ω=0.8,d=1,b=-0.5 时,平顶孤子的强度分布图;(b)图(a)孤子解 U2 的加噪传输图;(c)当 ω=0.05 时,单极灰孤子的强度分布图;(d)图(c)孤子解 U1 的加噪传输图;(e) ω=0.05,d=1,b=-0.4 时,两极灰孤子的强度分布图;(f)图(e)孤子解 U1 的加噪传输图Fig.5.Intensity distribution and propagation properties of flat-topped soliton,unipolar grey soliton and bipolar grey solitons;(a) Intensity distribution of flat-topped soliton when ω=0.8,d=1,b=-0.5;(b) propagation of soliton solution U2 with the white noise in panel (a);(c) intensity distribution of unipolar gray soliton when ω=0.05;(d) propagation of soliton solution U1 with the white noise in panel (c);(e) intensity distribution of bipolar gray solitons when ω=0.05 ,d=1,b=-0.4 ;(f) propagation of soliton solution U1 with the white noise in panel (e).
当耦合模式为三个高斯组合的函数形式,

β1=β2=-1,b=-0.4,d=0.2,α1=5,α2=6,ω=0.002时,得到图6(a)的三极灰孤子,图6(b)显示它的不稳定传输.把孤子间的距离拉大,即H=7,得到图6(c)所示的孤子分子.三极灰孤子即使增大孤子间的距离也不能稳定传输.当ω≤0.12时出现三极灰孤子,继续减小ω的值,则灰孤子的灰度越小,稳定性就越差.若ω>0.12 时,三极灰孤子变成三极暗孤子,当 0.3≤ω≤0.75 时三极暗孤子变成平顶孤子.

图6 三极灰孤子的强度分布和传输特性 (a)当 H=4 时,三极灰孤子的强度分布图;(b)图(a)孤子解 U1 的加噪传输图;(c)当 H=7 时,孤子分子的强度分布图;(d)图(c)孤子解 U1 的加噪传输图Fig.6.Intensity distribution and propagation characteristics of tripolar grey solitons: (a) Intensity distribution of tripolar grey solitons when H=4;(b) propagation of soliton solution U1 with the white noise in panel (a);(c) intensity distribution of soliton molecule when H=7;(d) propagation of soliton solution U1 with the white noise in panel (c).
3 结论
本文研究了非局域非线性熔融双芯平面波导耦合器中耦合模式与光孤子结构以及传播稳定性的内在关联性.首先,探究了非局域程度、传播常数、非线性参数和耦合宽度与基态类亮孤子的峰值、束宽、功率之间的关系,并且发现在多极类亮孤子中也存在类似的关系.研究表明,类亮孤子的功率随着非局域程度和耦合函数宽度的增大而增大,而随着传播常数的增大而减小,折射率总是在孤子峰值时达到最小.其次,通过改变耦合模式来控制孤子结构.若熔融耦合器的耦合模式为多个高斯函数的组合,调控耦合强度最大值位置,可以形成不同极数或者孤子间距离不同的多极类亮孤子或灰孤子.这样的模型相比于常耦合强度的薛定谔方程,可以通过改变耦合模式和调节耦合函数宽度,使得孤子解更丰富.通过牛顿迭代法,调控耦合模式得到多极类亮孤子、平顶孤子以及多极灰孤子.具有相同模式的多极类亮孤子、平顶孤子和灰孤子解在合适的参数下可以稳定传输,然而孤子峰值不相同的三极类亮孤子和三极灰孤子出现不稳定传输.减小耦合函数宽度,灰孤子的灰度变小,灰孤子的灰度越小越不容易稳定传输.调控耦合强度最大值位置,可以控制孤子间的距离,从而形成孤子分子.通过数值分析,发现类亮孤子和暗孤子相比灰孤子更容易实现稳定传输.最后,调节耦合函数宽度可以实现灰孤子、平顶孤子和暗孤子的转化.那么不同类型的孤子结构和孤子的转化将如何应用在光开关和逻辑门是一个值得探索的问题.
