不确定时滞LPV系统的鲁棒稳定性分析

刘玉忠, 李珊玉

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

0 引 言

线性参数变化(LPV)系统是一类时变系统,其状态空间模型的矩阵是某些时变参数的确定函数,而这些时变参数是可以实时测量的[1]。LPV系统的出现从某种意义上解决了复杂非线性系统的建模问题。近年来,LPV系统的控制方法已经广泛应用于实际工程中,如导弹自动导航、飞行控制、机器人控制等领域,成为控制理论中研究的热点问题[2-5]。

在LPV系统中,系统矩阵已含有参数不确定的部分,但实际建模过程中还有结构不确定性的存在,如测量误差、输入条件的变化、传感器等部件非正常工作及外界的干扰均会引起结构不确定性的出现[6-7]。此外,在各类工业系统中,时滞现象是很普遍的,如皮带传输、极缓慢的过程或复杂的在线分析仪等[8]。因此,对不确定时滞LPV系统的鲁棒稳定问题进行分析具有更实际的意义,这给研究工作带来相当大的难度。目前,对于不确定时滞LPV系统的研究结果还相当有限,而且大部分没有考虑结构不确定和时滞带来的影响。Apkarian等[9]通过优化方法设计线性变参数控制器,将线性变参数控制问题转换为鲁棒控制问题,Ilka和Vesely[10]提出一种基于线性参数变化的增益调度控制器的设计方法,Buzachero等[11]给出具有衰减率性能指标和控制器规范优化的连续时间不确定切换LPV系统控制的改进方法。Sun和Zhao[12]研究一类时变时滞切换系统的稳定性和L2增益问题,Wu和Grigoriadis[13]利用参数相关Lyapunov函数法,研究变参数时滞LPV系统的稳定性和诱导L2范数性能,Lu和Wu[14]利用多参数相关Lyapunov函数法研究LPV系统的切换控制问题,以提高系统性能和控制设计的灵活性,Sun等[15]针对有时变时滞的LPV系统,考虑时滞相关的H∞控制问题。

本文对一类不确定时滞LPV系统的鲁棒稳定性问题进行分析和研究,通过构造Lyapunov-Krasovskii泛函,利用Schur补性质,将矩阵不等式转化为LMI,然后引入二次型性能指标,分析系统的鲁棒性能,最后由于参数存在依赖性,利用近似基函数和网格技术的方法,将无限维的LMI转化为有限维的LMI,从而把不确定时滞LPV系统的鲁棒稳定性问题归结为线性矩阵不等式的求解问题。

1 问题描述

考虑如下的不确定时滞LPV系统:

(1)

假设实矩阵ΔA(ρ),ΔAd(ρ)具有如下不确定的形式:

其中:D(ρ),E(ρ),Ed(ρ)是已知适当维数的矩阵;F(ρ)∈Ri×j是满足FT(ρ)F(ρ)≤I的未知不确定参数矩阵。下面是本文用到的引理。

引理1[8]给定适当维数的矩阵Y,D,E,其中Y是对称的,则

Y+DFE+ETFTDT<0

对所有满足FTF≤I的矩阵F成立,当且仅当存在一个常数ε>0,使得

Y+εDDT+ε-1ETE<0

2 主要结果

本文主要研究不确定时滞LPV系统(1)的鲁棒稳定性问题。

定理1 如果存在标量ε>0,对称正定矩阵P(ρ),Q,其中P(ρ)为连续可微的矩阵函数,使得

(2)

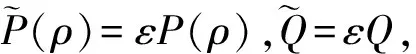
证明 选取Lyapunov-Krasovskii泛函为

(3)

V(x,ρ)沿着系统(1)轨迹的导数为

(4)

(5)

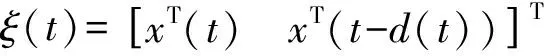
根据引理1可知,式(5)中的矩阵小于零,对所有满足FT(ρ)F(ρ)≤I的参数不确定性矩阵F(ρ)都成立,当且仅当存在一个标量ε>0,使得

整理得

(6)

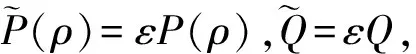
(7)

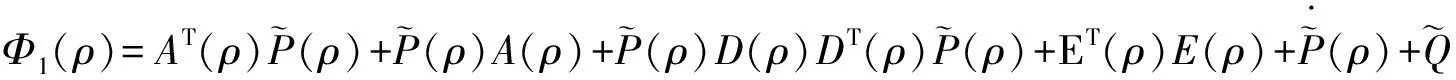
为分析系统的鲁棒性能,考虑一个二次型性能指标,其中S>0为给定的加权矩阵:

(8)

定理2 对系统(1)和性能指标(8),若存在对称正定矩阵P(ρ)和Q,使得对所有满足FT(ρ)F(ρ)≤I的参数不确定矩阵F(ρ)有

(9)

则系统(1)是鲁棒稳定的,且对于所允许的不确定参数不确定矩阵,性能指标(8)满足

证明 从矩阵不等式(9)可以推出

(10)

(11)

将式(11)左右两边从t=0到t=∞积分,并利用系统的鲁棒稳定性得

注1 定理2中的条件(9)不是关于变量P(ρ)和Q的线性矩阵不等式,下面将该定理的条件转化成一个容易检验的LMI的可行性问题。

定理3 对于给定的系统(1)和性能指标(8),若存在标量ε>0,对称正定矩阵X(ρ)和Q,使得

(12)

则不确定时滞LPV系统是鲁棒稳定的,且对所有允许的不确定性,性能指标满足

证明 与定理1的证明类似,矩阵不等式(9)对所有允许的不确定性成立,当且仅当存在标量ε>0,使得

(13)

应用Schur补性质,式(13)等价于

(14)

式(14)左右两边的矩阵分别左乘和右乘diag{P-1(ρ),I,I},记X(ρ)=P-1(ρ),则式(14)等价于

(15)

(16)

利用Schur补性质,(16)式等价于式(12),对式(12)左右两边的矩阵分别左乘和右乘矩阵diag{I,Q-1,I,I},记W=Q-1,则式(12)等价于

因此,系统(1)是鲁棒稳定的。

注2 由于在对Lyapunov函数求导时产生参数部分的导数项,导致线性矩阵不等式(2)和(12)是无限维的,利用近似基函数和网格技术,将其转化为有限维的线性矩阵不等式。选取近似基函数为fi(ρ),i=1,2,…,nf,则

3 结 论

文章研究了不确定时滞LPV系统的鲁棒稳定问题。构造L-K泛函,利用Schur补引理处理矩阵不等式,并引入二次型性能指标,分析了系统的鲁棒性能。利用近似基函数和网格技术的方法,将无限维的LMI转化为有限维的LMI,有效地解决了LMI的求解问题。