初中数学课堂中有效积累活动经验探究——以《二次函数与线段最值》一课为例

谷晓波 杜乙霞

初中数学课堂中有效积累活动经验探究——以《二次函数与线段最值》一课为例

谷晓波 杜乙霞

（延边州教育学院，吉林 延吉 133000）（敦化市第一中学校，吉林 敦化 133700）

数学活动经验的积累是提高数学素养的重要标志，帮助学生积累数学活动经验是数学教学的重要目标，是学生不断经历、体验各种数学活动过程的结果。学生通过以“以身体之，以心悟之”为特征的体验，积极参与主动探究结果，就会切身体验到探究数学学习的乐趣，在获得正确结论的过程中积累活动经验，为知识的延续打下坚实的基础。

初中数学教学；活动经验；积累

义务教育阶段数学课程的的总目标从“双基”发展到“四基”，从基础知识、基本技能增加了基本思想和基本活动经验。数学活动经验是学习主体通过亲身经历数学活动过程所获得的具有个性特征的体验，具有“主体性”“实践性”“发展性”和“多样性”等特征。基本的数学活动经验可分为直接的活动经验、间接的活动经验、思考的活动经验，学生只有积极参与教学过程，经过独立思考、探索实践、合作交流，才有可能真正积累活动经验，在这样的一个过程中，必然有情感态度价值观的体现。本文以二次函数中考综合题为切入点，通过对原题改编、变式、整合形成新的问题，进行一题多变训练，帮助学生构建数学知识体系，在课堂教学过程中很好地体现出学生积累活动经验的过程，切实提升课堂效率。

一、基础性问题引入利于积累直接活动经验

为使学生顺利掌握二次函数相关最值问题解决的通性通法，课前可以设置两个基础性的问题，使学生利用已有的直接经验经过独立思考能够直接作答，同时激发学习兴趣，初步感悟本节课要研究的内容。

对于问题1学生已有知识经验是最短路径知识迁移，因此都能顺利得解：

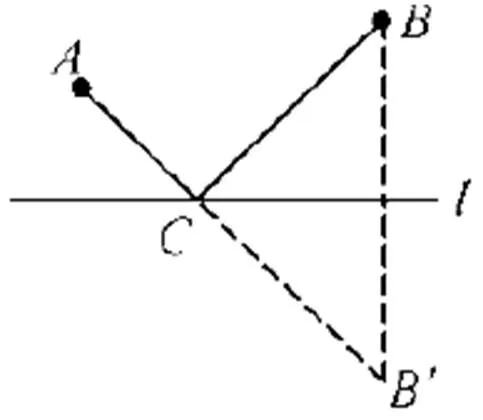
对于问题2，学生已有的知识经验是三角形的三边关系，利用已有的直接经验也能顺利得以解答三角形两边之差小于第三边,使A、B、P三点共线在解题过程中渗透数学中转化的思想（化折为直）

引导学生关注其中蕴含的思想方法及数学模型。将以往知识融入新课学习，以旧引新的过程促进学生积极的思维过程，正是学生以“以身体之，以心悟之”的主动学习，将直接经验有效利用的实践过程，为与线段最值问题的延续拓展学习打下基础。

二、开放性问题设置为积累间接经验创造条件

函数是描述现实世界变量之间关系的重要数学模型。初中数学研究了一次函数、二次函数、反比例函数，本节旨在二次函数的综合探究。运用二次函数可以解决许多问题，例如以二次函数为载体，求线段、周长，面积等的最值问题。函数问题是近年全国数学中考的一个热点，也是难点；与周长，面积有关的问题可以转化为与线段有关的最值问题。基于实际情况，由浅入深设置一个开放性问题：

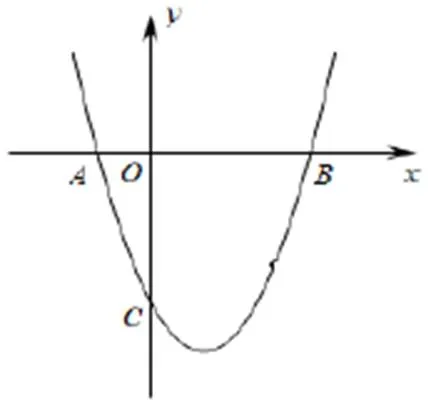
根据所给条件，你能解决哪些问题？

选一个正确的结论进行整理。

选取2019年吉林省中考题26题题干为探究主线，设置两个学习任务，一是学生利用已知条件，在不添加条件的基础上自主解决较简单的数学问题。由浅入深，为后续渐近式的变式训练打下基础。二是立足基础题通过添加点或线进行多角度变换，编拟出与线段有关的最值问题，根据问题建构数学模型，解决二次函数背景下的线段和、差等最值问题。设计此项活动的目的使学生明确数学是自然的，有效激发学生探究数学的积极性，学生通过主动探究掌握二次函数综合题型中关于线段最值问题的解题方法。

三、拓展性问题探究有效积累思考的活动经验

思考的活动经验是通过分析、归纳等思考获得的数学经验。结合问题3的研究结果，精心设置问题，及时拓展所学内容，独立思考已无法全面解决此类问题，经过合作交流，共同探索实践，逐步达到对数学知识的意会、感悟，积累解决和分析问题的经验，将这些经验迁移到后续的数学学习中。

问题4：在所给出的抛物线中适当添加点或线段或直线，在组成的新图形中你有什么发现？写出你发现的结论.

学生在图中添点或线，观察、猜想、探索、交流、归纳，亲自经历知识的形成过程。

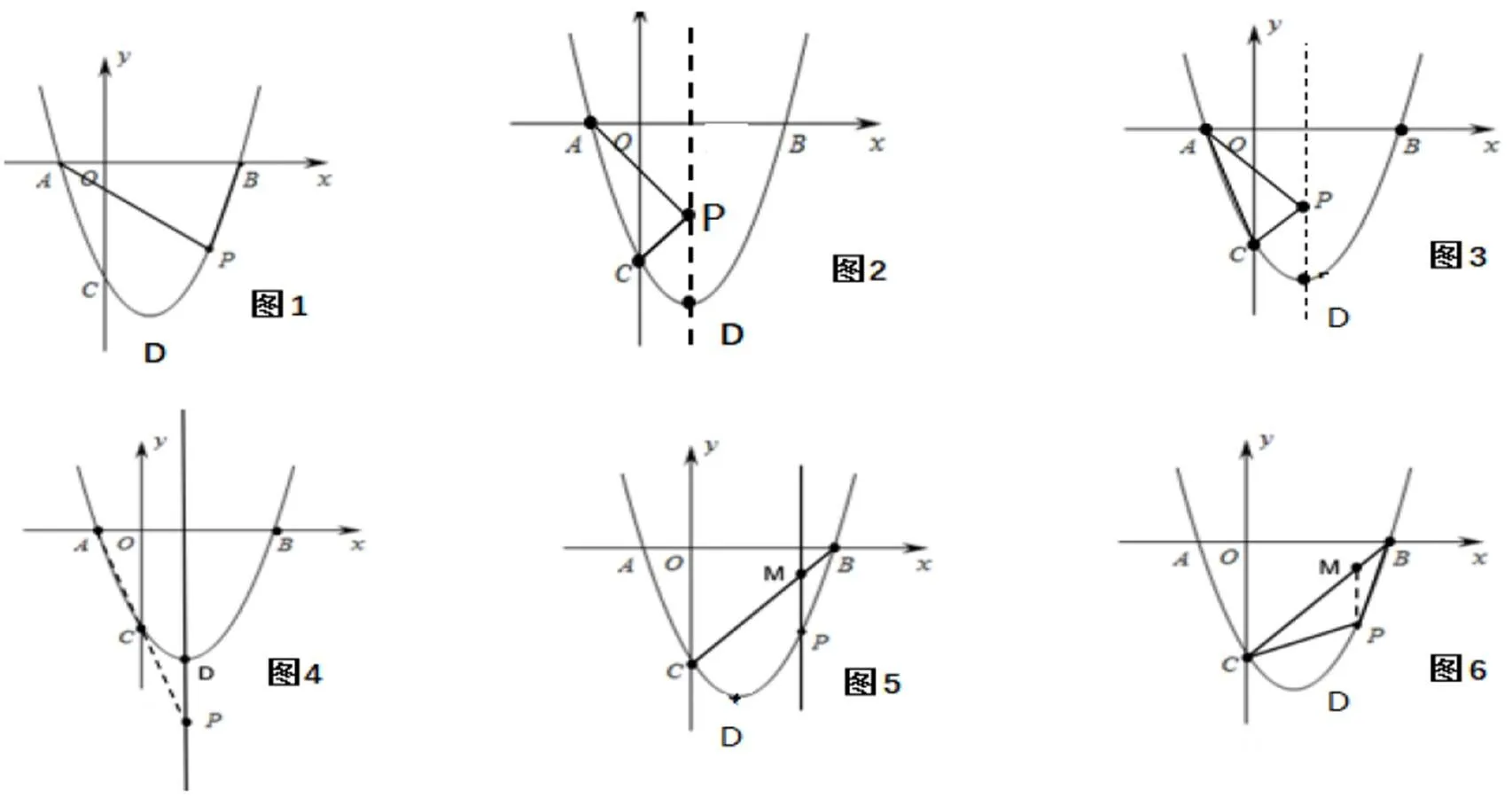
针对此拓展性问题，学生在仔细研究后，结合前面的已有知识基础及经验，生成以下结果：

1.点P位于x轴下方的一个动点，求△ABP面积的最大值（如图1）。

2.在抛物线的对称轴上找一点P，使PA+PC最小（如图2）。

3.在抛物线的对称轴上找一点P，连接AC,PA,PC,使△ACP周长最小（如图3）。

4.抛物线的对称轴上找一点P，使得|PA－PC|最大（如图4）。

5.直线BC下方的抛物线上有一点P，过点P作x轴的垂线，交BC于点M，当点P运动到何处，PM有最大值（如图5）。

6.线BC下方的抛物线上有一点P，过点P作x轴的垂线，交BC于点M，当点P运动到何处，ΔPBC的面积有最大值（如图6）。

以上结论的得出,源于经验的积累,同时教师及时点拨归纳体现出数学内在的规律:

立足基础题，通过添加点或线进行多角度变换，注重一题多解训练，培养学生提出问题和解决问题的能力。体会及感悟化归与转化、数学建模等数学思想方法。有了合作过程中的自然交流，学生的学习就处于高度生成的状态，此时教师的适时点拨与提醒，不是去刻意地讲授与引导，是进行数学思维训练的良好契机，数学是思维的体操，在特定的数学情境中设置数学活动，学生在探究的过程有效积累了思考的活动经验，这种注重数学知识的生成，把碎片化的知识点有效串联成系统，注重知识的整体构建，学生明确数学问题的来龙去脉，真正做到知其然，知其所以然，到何由知其所以然。

四、精心设置有效数学活动使学生真正积累数学活动经验

有效的数学活动很容易造成的错觉就是“活动”就要动手实践、合作、小组讨论，其实数学学科的特点决定了数学活动本身有着与其他学科不同的特点。数学活动首先是“数学”的，所从事的活动要有明确的数学目标，是否需要动手实践及小组合作和互相交流是一种形式上的反映，而通过活动对数学的深化理解，对数学在实际应用的理解是非常重要的，其实一道数学综合题的分析及解决过程就是一个真实有效的数学活动。在前面问题已经解决的基础上，适时呈现本节的核心问题。

问题5：如图，抛物线y＝（x﹣1）2+k与x轴相交于A，B两点（点A在点B的左侧），与y轴相交于点C（0，﹣3）．P为抛物线上一点，横坐标为m，且m＞0．

（1）求此抛物线的解析式；

（2）当点P位于x轴下方时，求△ABP面积的最大值；

（3）设此抛物线在点C与点P之间部分（含点C和点P）最高点与最低点的纵坐标之差为h．

①求h关于m的函数解析式，并写出自变量m的取值范围；

②当h＝9时，直接写出△BCP的面积．

本题是二次函数的一个综合试题 ，围绕二次函数核心知识进行考查， 每一个问都在增加区分度，真正达到选拔功能。发展了学生的函数思想, 分类思想、数形结合思想、方程思想等，为学生高中后续的学习提供方法和活动经验。教师根据学生生成的问题，呈现此题，设计引发学生深入思考的的问题，唤醒学生的深思考与真体验，引导学生深度学习，在此过程中及时培养学生数学思维的延伸。

波利亚解题研究发现，一个比较综合的问题一般都能分成若干个基本的小问题，当然，一系列基本问题也能组合成比较复杂的问题。通过此题设置活动，学生在研究的过程中有效积累数学活动经验。学生对此题的研究中发现考查的知识点虽然很多，但是有了前面问题由浅入深的层层剖析，学生对综合题的形成有了深刻的理解，利用已有的活动经验能够分析问题，解决问题。

总之，数学活动经验不仅仅是实践的经验，也不仅仅是解题的经验，更重要的是思维的经验，是数学活动中思考的经验。获得数学活动经验最重要的是积累发现问题、提炼问题的经验，以及分析问题、解决问题的经验，学生掌握数学思想，也需要在数学活动经验的积累上形成。因此，教师要精心设置数学活动，为学生积累数学活动经验创设氛围，使学生学生在经过独立思考，勇于探究的过程在获得数学活动经验。

[1]史宁中.义务教育数学课程标准（2011年版）解读[M].北京：北京师范大学出版社，2016.

[2]张奠宙.可以说“中国数学教育崛起”吗？[J].初中数学教与学,2017(6):3-5

[3]周立志.开放设问 变式探究积累经验[J].初中数学教与学，2017（6）：39-43.

2020—09—12

G633.6

A

1673-4564（2020）05-0215-04