以一节章末复习课的教学设计为例谈数学核心素养的培养

秦泗伟

以一节章末复习课的教学设计为例谈数学核心素养的培养

秦泗伟

（延边第二中学，吉林 延吉 133000）

正方体模型在高中立体几何教学中具有非常重要的地位，教师教学中借助于实物模型展示，研究模型，帮助学生建立模型感和空间感，有利于学生获得模型解题经验，有利于发展学生的数学建模核心素养。

立体几何；正方体；数学模型；核心素养

人教A版教材必修二的第一章中，学生从整体观察入手，认识空间几何体，在这个基础上，第二章教学以长方体为载体，在直观感知的基础上学习空间上直线、平面的位置关系，空间中平行和垂直关系的转化，距离和空间角的求解等重要知识，从三点共线、共面的证明、空间直线的位置关系、线面平行、平面平行、线面垂直、面面垂直的证明，再到距离、空间角的求解、正四面体外接球、三视图等问题，正方体都是考查知识的重要载体。

一、教材习题来源

正方体模型作为特殊的长方体，在教材的例题和习题中出现了很多次。

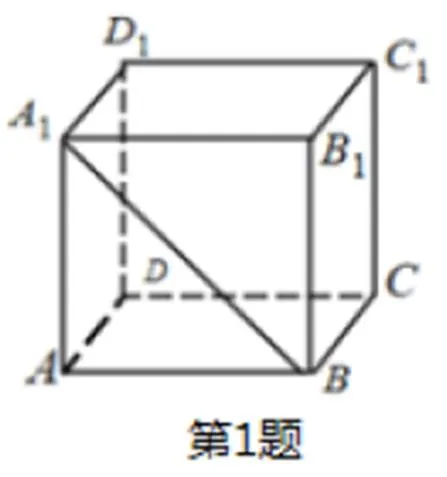
1.（人教A版数学教材必修二47页例3）

2.（人教A版数学必修二52页B组练习1）

如图是正方体的平面展开图，则在这个正方体中：

以上四个命题中，正确命题的序号是_______

3.（人教A版教材数学必修二52页B组练习2）

4.（人教A版教材数学必修二56页练习2）

5.(人教A版教材数学必修二57页例2).

6. （人教A版教材数学必修二58页练习2）

7.（人教A版教材数学必修二74页A组7题）

8.(人教A版教材数学必修二74页B组1题)

9.（人教A版教材数学必修二78页A组第4题）

正方体棱长为a，点C,D分别是两条棱的中点证明：四边形ABCD是一个梯形，并求出四边形ABCD的面积。

10.( 人教A版教材数学必修二79页B组第2题)

二、教学过程

（1）有几个面？几条棱？几条面对角线？几条体对角线？几个对角面？成异面直线的棱有几对？

（2）体对角线与面对角线的位置关系？相邻两个面内的两条面对角线所成角是多少？

(3)如何证明直线与平面平行？

（4）正方体的截面有哪些可能？你能画出截面吗？

（5）如何证明直线与平面垂直？平面与平面垂直呢？

（6）如何求两个平行平面之间的距离?

（8）棱长为a的正四面体的外接球半径是多少？

问题1.正方体6个面、12条棱、4条体对角线、6个对角面、成异面直线的棱24对。

通过连上相对面的面对角线，可以快速帮助学生数出对角面的个数。与棱AB异面的棱有4条，12条棱共有48对，因为异面直线成对出一共有24对。

引导通过问题1和问题2，在直观感知的基础上，准确认识正方体模型的基本要素，准确把握空间上两条直线的位置关系，尤其是加深对异面直线概念的理解，理解两条异面直线所成角的定义，加深对空间上两条直线垂直（相交垂直和异面垂直）概念的理解。借助线线与线面垂直关系的转化可以完成证明。

问题3.空间中平行关系的转化关系涉及6个定理，具体关系如下图，教学中要理顺三种平行关系的转化（图2），其中线面平行是关键，而线线平行是基础，要会用图形语言和符号语言准确表达定理。通常构造中位线（图3）和平行四边形（图4）来证明线线平行。正方体中比较重要的两个平行平面（图5）是等边三角形，具有严格的对称性。

问题4.面面平行的性质定理可以得到线线平行，它是作截面常用的依据。可以分析出正方体中常见的截面有三角形、四边形、五边形和六边形。而最常考查的是正六边形截面，结合公理3可以作出截面与表面的交线。

问题8.正方体和正四面体具有严格的对称性，可以采用“割补法”寻找二者之间的联系，这种转化大大降低了难度。

问题9.两道高考真题练习(略)

三、教学思考

1.准确把握课程目标，怀有一颗“同理心”

在高一立体几何的教学中，教师要准确把握课程目标，不随意增加教学难度，对学生要有一定的“同理心”，真正了解学生的现实情况，尽可能的替学生考虑，放慢节奏，降低难度。教学中要借助大量的实物模型教具，引导学生通过直观感知、操作确认初步认识空间几何体，初步认识空间中点、直线、平面之间的位置关系；通过对大量图形的观察、实验、操作和说理，使学生进一步了解平行、垂直关系的基本性质以及判定方法，学会准确地使用数学语言表述几何对象的位置关系，初步体验公理化思想，培养逻辑思维能力，并用来解决一些简单的推理论证及应用问题。

2.研读教材知识重组，发展数学有效思维

阶段复习课不等同于新授课，与高三的专题复习课类似，要求将知识点集中再现，甚至要完全打乱重组。教师要认真研读教材，将零散的知识片段重新整合成一个生态系统。在一节课堂里将教材中的10个例习题和2道高考真题融会贯通，巧妙融合在一个模型里，通过设置疑问，引导学生层层递进，从而达到复习核心知识的目的。有利于学生体会知识之间的内在联系，发现数学问题的本质特征，达到以点带面的复习效果，这对发展学生的思维品质和提高学生的学法指导都是非常有利的，但是需要一线教师付出更多的努力。

3.探究立体模型，发展数学建模核心素养

立体几何的教学离不开几何体，教学中以长方体为载体，可以帮助学生在直观感知的基础上发展几何直观能力。而作为特殊的长方体，正方体是教学中非常重要的载体，它几乎包含了全部考点，蕴含了立体几何中最基本、最核心的知识点，有着丰富的平行和垂直、距离和角度问题，揭示了平面和空间，二维和三维空间的转化。用好模型开展教学，可以培养学生的数学建模、解模、用模的意识，更好地揭示数学问题的本质。在立体几何教学中，采用模型教学不但可以培养学生运用图形语言进行交流的能力和严谨的推理论证能力，更重要的是可以发展学生的数学建模核心素养。除了正方体，长方体中的堑堵、阳马、鳖臑模型等都非常值得探究。

总之，努力提高高中数学课堂教学的有效性是每一个教师的追求，采用高效的教学方式，不等同于题海战术，是在题海中提炼出问题的本质，教师不仅要讲清题目本身，探索解题思路，而且要帮助学生发现解题模型，进行破题指导，制定最佳的解题方案，优化解题策略，这是取得教学成绩的保证。

附：本文图汇总

2020—04—06

G633.6

A

1673-4564（2020）05-0261-03