以权函数分担一个公共值集的亚纯函数唯一性
2020-12-03李荣慧陈亦佳
李荣慧,陈亦佳
(1.云南师范大学 数学学院,云南 昆明 650500;2.玉溪师范学院 数学与信息技术学院,云南 玉溪 653100)
1 引言及主要结果

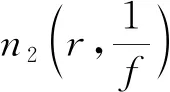


根据定义1和定义2我们有如下两个定义:


F.Gross和杨重骏在文献[4]中证明了定理:
定理A[4]集合S={z|ez+z=0}是整函数的CM型唯一性象集.
注意到定理A中的集合S是一个无限集.
1976年,F.Gross在文献[5]中提出这样一个问题:
问题1[5]是否可以找到一个有限集合S,使得对于∀非常数整函数f(z)和g(z),若Ef(S)=Eg(S),则是否有f(z)≡g(z)?
1993年,仪洪勋在文献[6]中构造出了含有15个元素的整函数的CM型唯一性象集,给F.Gross提出的问题一个肯定的回答,并于1995年在文献[7]中建立了含有7个元素的整函数CM型唯一性象集,且在文献[8]中构造了一个含有11个点的亚纯函数唯一性象集.仪洪勋还提出下述待解问题:
问题2[8]能否找到一个元素少于11的亚纯函数唯一性象集?
定理B[7]集合S={z|z7+z6+1=0}是一个含7个点的整函数CM型唯一性象集.

2008年,熊坚在其毕业论文中利用权分担的思想得到了“几何个数”为9的亚纯函数唯一性象集[9].
本文中,我们利用权分担的概念继续研究关于亚纯函数唯一性象集的元素个数问题.得到了如下结果:
定理1 设P(z)=36z10-80z9+45z8-1.P(z)以1为3重零点,而其余零点均为单零点,设其判别的零点集为S={1,a1,a2,…,a7},且τ:S→N+,其具体的表示如下:
τ(1)=3,τ(ak)=1,(k=1,2,…,7),
如果非常数亚纯函数f(z)与g(z)以τ:S→N+为权函数CM分担S,且Θ(∞,f)>λ,Θ(∞,g)>λ(其中λ>0).则f(z)≡g(z).
2 几个引理

T(r,R(f))=max{p,q}T(r,f)+S(r,f).

T(r,Q(f))=pT(r,f)+S(r,f).
引理3[9]设q为不小于2的整数,cj(j=1,2,…,q-1),∞是q个两两判别的复数.如果非常数亚纯函数F(z)与G(z)以∞为CM分担值,则如下两个结论之一必定成立:
(2)∃有限常数A和B,使得A≠0,F(z)=AG(z)+B且
#({c1,c2,…,cq,∞}∩{Ac1+B,Ac2+B,…,Acq+B,∞})≥2.
引理4[8]设φ(w)=(n-1)2(wn-1)-(wn-2-1)-n(n-2)(wn-1-1)2,则
φ(w)=(w-1)4(w-ζ1)(w-ζ2)…(w-ζ2n-6).

3 定理1的证明
由已知条件知
P(z)=(z-1)3Q7(z),Q7(1)≠0,
(1)
P(z)+1=z8Q2(z),Q2(0)≠0,
(2)
其中,Q7(z)36(z-a1)(z-a2)…(z-a7),Q2(z)=36z2-80z+45,
令
(3)
从而由引理1得
T(r,F)=10T(r,f)+S(r,f),
(4)
T(r,G)=10T(r,g)+S(r,g),
(5)
由f(z)与g(z)以τ:S→N+为权函数CM分担S可得F(z)与G(z)以∞为CM分担值.
又由(1)(2)式及引理1知
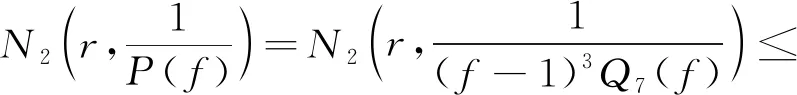
(6)
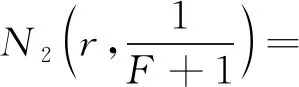
(7)
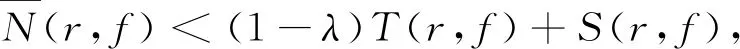
(8)
从而由(4)(6)(7)(8)诸式有
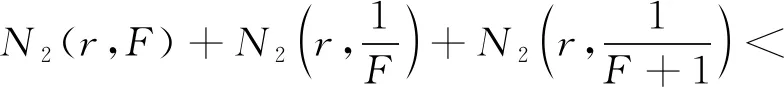
(9)
同理可得
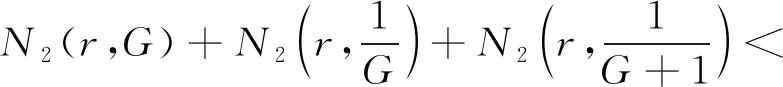
(10)
故由(9)(10)式得
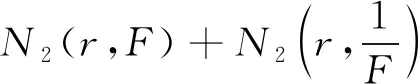
(11)
又由引理3和(11)式得
这显然是不可能的.所以∃常数A和B,使A≠0,且
(12)
由(12)式得
T(r,f)=T(r,g)+O(1).
(13)
以下分3种情形讨论:
情形1B≠0.
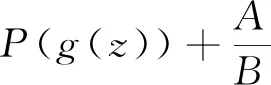
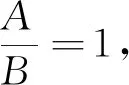

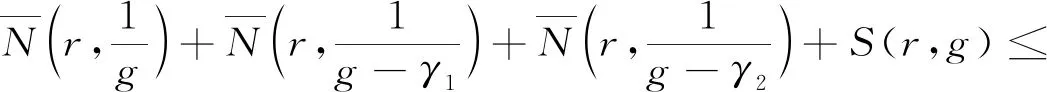
显然,这是一个矛盾.
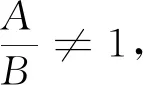
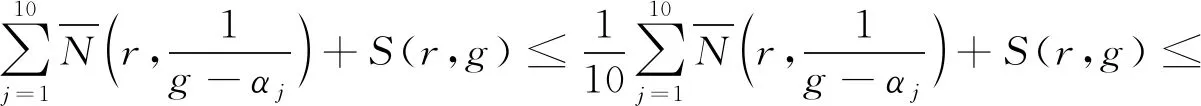
T(r,g)+S(r,g),
这也是一个矛盾.
情形2B=0,且A≠1.
这时,由(2)和(12)式得
(14)

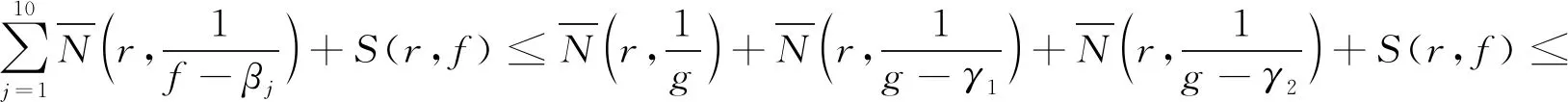
3T(r,g)+S(r,f)≤3T(r,f)+S(r,f),
这是一个矛盾.
情形3B=0,A=1.
此时,有P(f(z))≡P(g(z)),即
36(f10(z)-g10(z))-80(f9(z)-g9(z))+45(f8(z)-g8(z))≡0.
(15)
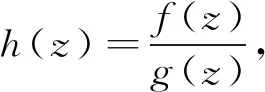
36(h10(z)-1)g2(z)-80(h9(z)-1)g(z)+45(h8(z)-1)≡0.
(16)
若h(z)≡const,则由g(z)为非常数亚纯函数及(16)知:h10(z)≡1,h9(z)≡1,从而h(z)≡1,故f(z)≡g(z).
若h(z)≢const,则(15)式可改写成
其中φ(h(z))=81(h10(z)-1)(h8(z)-1)-80(h9(z)-1)2故由引理4知:
(17)

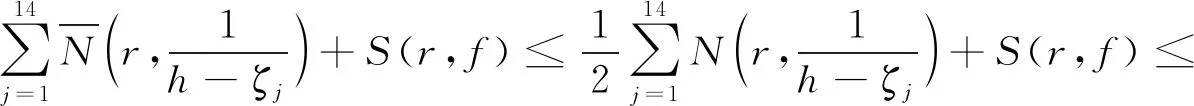
7T(r,h)+S(r,h),
这是矛盾的.
综上所述可得f(z)≡g(z).定理1证毕.
