基于改进飞蛾扑火算法的微带天线设计优化

秦 天，项铁铭，李蓓蓓

(杭州电子科技大学电子信息学院，浙江 杭州 310018)

0 引 言

飞蛾扑火优化(Moth-Flame Optimizer，MFO)算法是由澳大利亚学者S.Mirjalili提出的一种群智能优化算法[1]。算法的设计来源于飞蛾围绕火焰的飞行行为，在诸多工程优化领域得到验证。例如，王光等[2]提出一种基于折射原理反向学习的飞蛾扑火算法，引入历史最优火焰平均值、反向学习策略和折射操作，使火焰间的信息能够互相交流并具备跳出局部解的能力；S.Yasir等[3]以MFO算法为中心，提出聚类算法来优化网络问题；O.Ceylan等[4]使用MFO算法对电容器尺寸和分配进行建模，改善了电压分布问题；N.Muangkote等[5]使用MFO算法来优化卫星图像的最优多级阈值。

随着无线通信技术的广泛应用，微带天线的理论和技术日益成熟。微带天线具有剖面薄、体积小、重量轻、成本低和易集成等优势，广泛应用于各种移动和小型化通信设备[6]。然而，微带天线也存在损耗大、带宽较窄等缺点，所以，采用优化算法设计天线较传统天线设计方法更有优势。本文采用佳点集、越界重置、引力搜索和柯西变异等策略，解决标准算法中寻优速度慢、精度低等缺陷，提出一种改进的飞蛾扑火算法，最后通过改进算法实现对微带天线结构的优化。

1 基础理论

1.1 标准飞蛾扑火算法

MFO算法中，飞蛾根据火焰位置，采取横向定位机制螺旋围绕火焰飞行，先依靠火焰位置进行全局搜索，然后逐渐减少火焰数量进行深度挖掘，通过动态调整火焰数量和自适应路径搜索系数来平衡全局和局部的开发能力。

假设飞蛾的位置为M，火焰的位置为F，飞蛾围绕火焰飞行的位置更新函数为：

S(Mi,Fi)=Dijeb δcos(2πδ)+Fj

(1)

式中，Dij为第i个飞蛾到第j个火焰的距离，Dij=|Fj-Mi|，b=0.5，其大小决定螺旋轨迹形状的大小，δ为1个属于[-1,1]的随机数。

火焰数量随着迭代次数增加而线性递减，公式如下：

(2)

式中，N为初始火焰数量，T为迭代总数，l为当前迭代数。

2 改进飞蛾扑火算法

2.1 佳点集初始化

标准飞蛾扑火算法采用随机的方法来初始化种群，盲目的初始化行为直接影响解的质量，导致每次优化的结果出现2个数量级的浮动，甚至直接丢失较优解。文献[7]将佳点集理论和蜻蜓算法结合来改进算法，使种群的分布有了很大的改善，寻优效果取得显著提升。为了弥补标准MFO算法中初始化的不足，本文引入文献[8]提出的佳点集理论，将佳点集理论与飞蛾扑火算法结合。Gs为S维欧式空间中的单位立方体，且r∈Gs，则有：

(3)

若式(4)偏差满足

φ(n)=C(r,ε)n-1+ε

(4)

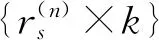
2.2 越界重置策略

位于边界上的飞蛾容易在之后的迭代中飞出边界产生无效解[9]，标准飞蛾扑火算法对越界飞蛾的处理方法是将越界个体拉回边界[10]。本文在处理越界飞蛾时，将处于解空间之外的飞蛾进行随机重置，重新进行解空间的探索，提高算法效率。改进的个体位置更新公式如下：

Xnew=l+C×(u-l)

(5)

式中，u和l分别为解空间的上界和下界，C∈[0,1]是一个随机变量。

2.3 混合引力搜索算法

引力搜索算法(Gravitational Search Algorithm, GSA)[11]的主要机制是不同粒子有不同的质量，适应度值越小的粒子其质量越大，根据粒子间的距离与质量决定引力关系。本文算法将GSA算法与MFO结合，在引力搜索过程中，通过火焰之间由质量(适应度值)引起的相互引力产生信息传递，对火焰位置进行改变，该运动遵循万有引力定律。

适应度值间接代表火焰的惯性质量，火焰惯性质量越大，吸引力越强，并且火焰运动变慢，表明火焰附近有更优的解。设火焰i在t时刻的质量为Mi(t)，火焰j对火焰i之间的万有引力定义为：

(6)

式中，火焰之间的欧式距离用Rij(t)表示，为了防止式中分母为0，加入一个非常小的ε常数，G(t)为t时刻的引力系数。式(6)为标准引力搜索算法对应的飞蛾扑火模型公式，为了找到下一代合适的火焰个体位置，对标准引力系数进行修改，重新定义的公式如下：

(7)

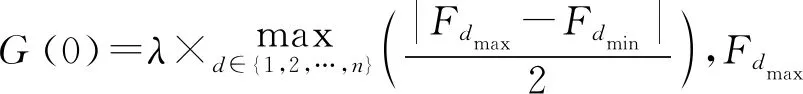
为了在迭代后期平衡算法的探索能力和开发能力，本文加入质量衰减算子γi(t)，质量更新为：

(8)

式中，f(Fbest)表示目前最佳适应度值，f(Fi)表示种群中火焰个体的适应度值。当飞蛾适应度值较差时，γi(t)小于1，进而降低火焰在群体中的权重，使目标向权重大的火焰前进。

假设火焰的初始速度为0，那么火焰i的位置更新公式如下：

(9)

式中，randj为[0,1]之间的随机数，Fi(t)为当前火焰的位置。

2.4 柯西变异策略

标准MFO算法中，算法本身不具备跳出局部最优的能力，导致算法早熟，收敛精度差。本文采用一种柯西变异的方法[12]，当迭代过程中，飞蛾的位置停滞不前时，个体进行柯西变异，继续向全局最优靠近，此时飞蛾群体中最优个体不进行变异以保证当前最优不被丢失。

柯西变异在每次迭代计算时，通过柯西分布函数产生1个均值为0，标准差为1的柯西变异矩阵，将得到的结果点乘待变异飞蛾的每一维作为更新步长。本文在式(1)基础上引入变异公式：

Xnew=ω×Cauchy(1,0)×[Dieb δcos(2πδ)+Fj]

(10)

式中，Cauchy(1,0)表示γ=1,x0=0的柯西分布，Fj为待变异飞蛾的位置，ω影响柯西变异的范围，ω更新公式如下：

ω=α(ub-lb)

(11)

式中，α为一个随迭代次数变化而变化的参数，ub和lb分别表示解空间的上界和下界。可以看出，飞蛾进行柯西变异的范围随迭代次数的增加而增加，所以，可以在算法停滞期为飞蛾扩展更大的搜索空间，增加种群的多样性。

3 设计实例

本文通过窄缝开槽微带天线的优化设计，验证改进标准MFO算法后的效果。窄缝开槽微带天线设计要求为：天线在4.7～5.3 GHz频段内的回波损耗尽可能低，并且端口隔离度应在-35 dB以下。因此，将待优化的目标函数设置为：

(12)

(13)

(14)

式中，S11i和S22i分别为端口1、端口2在第i个频率采样点的回波损耗，k为3，即每个端口在4.7 GHz，5.0 GHz和5.3 GHz频率处的采样点个数，当回波损耗在-10 dB以下时，适应度函数采用回波损耗实际值，有利于找到更优解，当回波损耗在-6～-10 dB之间时，解相对较差，因此给适应度函数赋0，令其评价结果变差，小于-6 dB时，结果不理想，抛弃该解，因此适应度值很大。S21i为采样点i处的端口隔离度值，μ为惩罚因子，当端口隔离度较差时，应将适应度值变差，故μ的值应尽量大，经测试这里设为103较合适。

4 仿真实验与结果分析

4.1 算法对比分析

本文在Windows10 R5-3500U，MATLAB R2019b环境下，选用表1中的3个测试函数，分别对蜻蜓算法(Dragonfly Algorithm，DA)、标准飞蛾扑火算法MFO和本文提出的改进飞蛾扑火算法MSMFO进行测试对比，3种算法均采用相同设置：维度D=10，种群数40，迭代次数500次，对每个测试函数进行30次独立运行。

运行后的适应度值如表2所示。

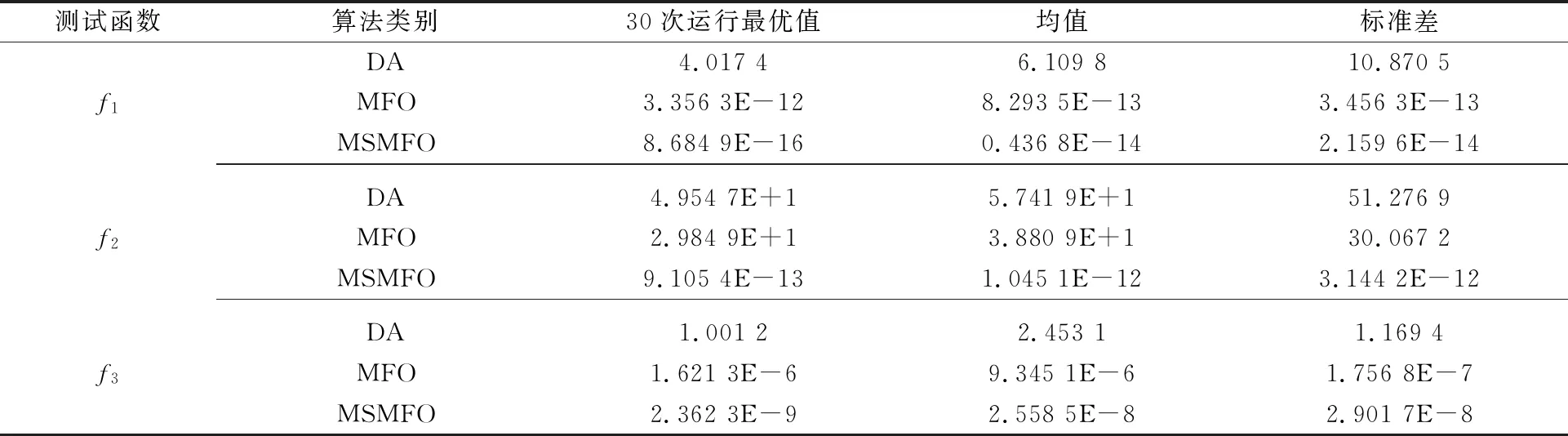
表2 不同算法测试结果对比

从表2可以看出，在整个测试过程中，DA算法性能较差，收敛不足且易陷入局部最优，而MFO算法优于DA算法，能在收敛精度和速度上优于DA算法，MSMFO算法在3个测试函数中均取得相对满意的结果。

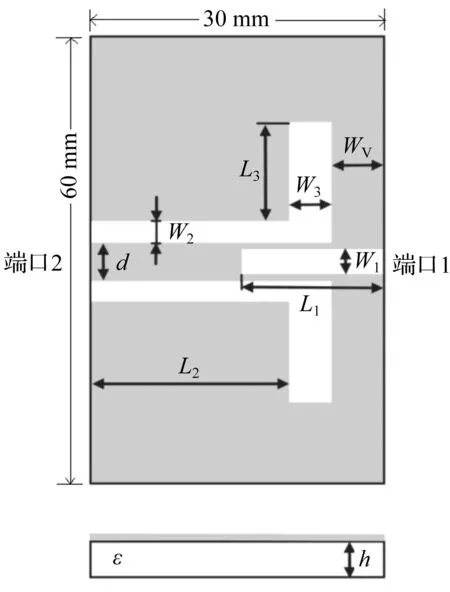
图1 开槽微带天线结构

4.2 窄缝开槽微带天线

文献[6]采用传统天线设计方式设计了一款双端口开槽天线，其结构如图1所示。为了构造具有高端口隔离度的紧凑型缝隙天线，端口1为同轴馈电，端口2为共面波导馈电，并将开放式的缝隙嵌入到共面波导的内导体中。该天线工作于5 GHz频段，介质基板采用FR4环氧树脂板，相对介电常数ε=2.2，厚度h=1.8 mm，辐射贴片和基板的尺寸相同，均为60 mm×30 mm，辐射贴片的右侧中心处开有一开端开放的矩形缝隙，长L2=19 mm，宽L2=19 mm；辐射贴片的左侧开有2个一端开放的L形缝隙，尺寸大小相同，且关于矩形缝隙轴对称设置。L形缝隙的水平臂长L2=19 mm，宽W2=1 mm，垂直臂长L3+W2=19 mm，宽W3=3 mm，与边界间距WV=8 mm。

4.3 实例分析

采用改进算法MSMFO对天线进行优化，天线尺寸参数作为待优化目标，设置种群规模为30，空间维度为5，迭代次数为500次，经算法寻优迭代后得到参数L1,L2,L3,WV,W2与优化前数据对比，结果如表3所示。

表3 算法优化结果

将改进算法优化后的数据、文献[6]数据和MFO算法优化后的数据进行HFSS建模仿真，得到端口1和端口2的回波损耗曲线如图2所示。

由图2可看出，端口1中，改进算法优化后的回波损耗在5 GHz附近有所降低，达到-26.933 1 dB，比文献[6]的回波损耗好很多，并且远优于标准MFO算法，-10 dB和-20 dB处的带宽均有所展宽，中心频率处的回波损耗有6 dB左右的下降。端口2中，改进算法的回波损耗达到约-31.537 6 dB，在-20 dB处的带宽较文献[6]有明显改善，总体上，改进算法的回波损耗和带宽比文献[6]有很大的改善，并且优于标准MFO算法优化的结果。改进算法优化后的天线在5 GHz谐振频率下的远场辐射图如图3所示，H面近似为椭圆形，E面为“8”字形，天线全向性较好。

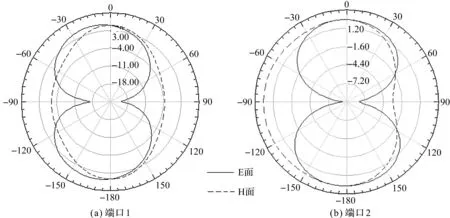
图3 端口的远场方向图

双端口天线在优化过程中虽然可以取得较好的方向图效果，但是仍需要考虑一个重要的因素即端口隔离度，由于天线的一个端口嵌入到另一端口的对称开口槽臂空隙中，因此极易导致端口间的干扰，隔离度降低进而影响天线性能。文献[6]数据、MFO算法和改进算法优化后的天线隔离度对比如图4所示。由图4可知，天线在5 GHz处，文献[6]数据中的隔离度值在-26 dB附近，MFO算法优化后的结果有所提升，而改进算法优化后的值可以达到-40.5 dB左右，降低了14.5 dB，有更高的端口隔离度，天线具备更好的辐射性能。

图4 天线端口隔离度对比曲线

5 结束语

本文采用佳点集、越界重置策略、引力搜索算法和柯西变异策略改进了标准飞蛾扑火算法，并将改进算法应用于窄缝微带天线的优化，一定程度上提升了天线的性能，解决了传统优化方法低效率和低精度的问题。然而，改进算法在寻优迭代时耗费的时间不可忽略，后期研究将考虑采用代理模型和改进算法相结合的方式，发挥精度和速度的优势的同时，提升算法的寻优效率。