用样本估计总体 为未来谋划发展

周华军

统计的基本思想是用样本估计总体，它主要研究两个基本问题：一是如何从总体中抽取样本，二是如何通过对所抽取的样本进行计算和分析，从而对总体的相应情况作出推断，为未来的发展规划提出合理建议。下面老师从2020年中考题中选取两例，说明统计的基本思想——如何用样本去估计总体。

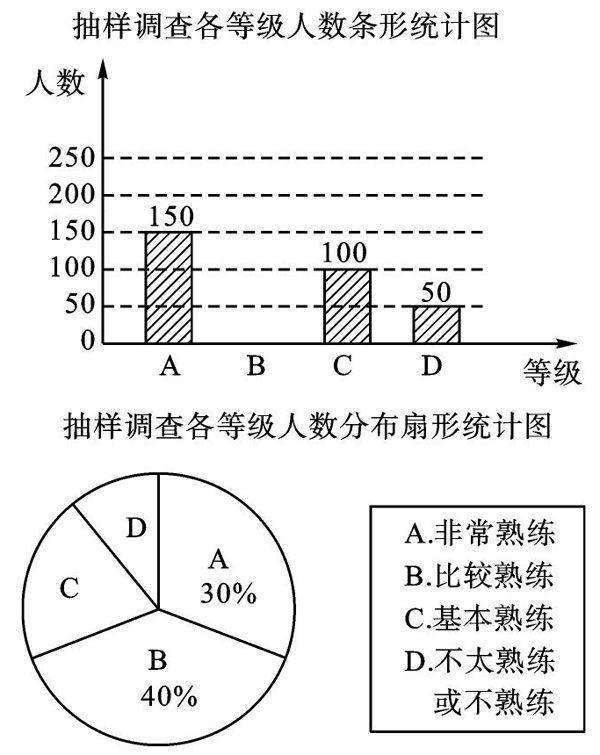
例1 （2020·江苏扬州）扬州教育推出的“智慧学堂”已成为同学们课外学习的得力助手。为了解同学们“智慧学堂”平台使用的熟练程度，某校随机抽取了部分同学进行调查，并将调查结果绘制成如下两幅尚不完整的统计图。

根据以上信息，回答下列问题：

（1）本次调查的样本容量是__，扇形统计图中表示A等级的扇形圆心，角为____°;

（2）补全条形统计图;

（3）学校拟对“不太熟练或不熟练”的同学进行平台使用的培训，若该校有2000名学生，试估计该校需要培训的学生人数。

【分析】（1）本题以两种统计图的形式描述数据，我们首先要从图中获取数据信息。根据条形统计图中A等级的人数，扇形统计图中A等级的所占百分比，求得样本容量，进而计算出扇形统计图中表示A等级的扇形圆心角的度数。

（2）根据（1）中得到的本次调查的样本容量，结合扇形统计图中B等级所占百分比，计算出B等级的人数，从而可以将条形统计图补充完整。

（3）根据条形统计图中提供的样本数据去估算全校需要培训的学生人数。

解：（1）本次调查的样本容量是150÷30%=500.

扇形统计图中表示A等级的扇形圆心角为360°×30%=108°。

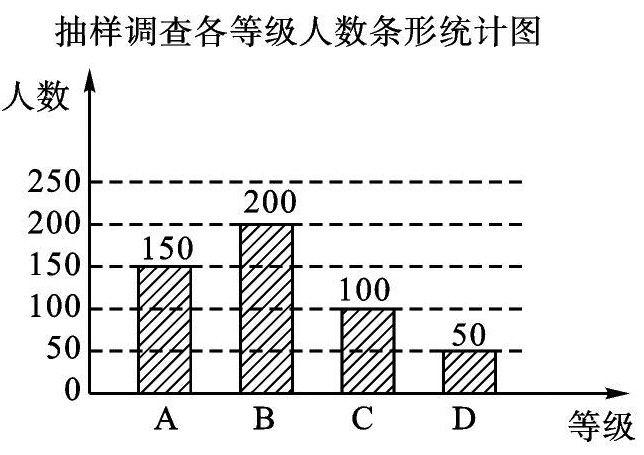
（2）B等级的人数为500×40%=200（人）。

补全的条形统计图如下图所示;

（3）2000×50/500=200（人）。

答：该校需要培训的学生估计有200人。

【点评】本题考查条形统计图、扇形统计图、用样本估计总体，从统计图中获取数据和数量之间的关系是解决问题的前提。用样本估计总体是统计中常用的思想方法。

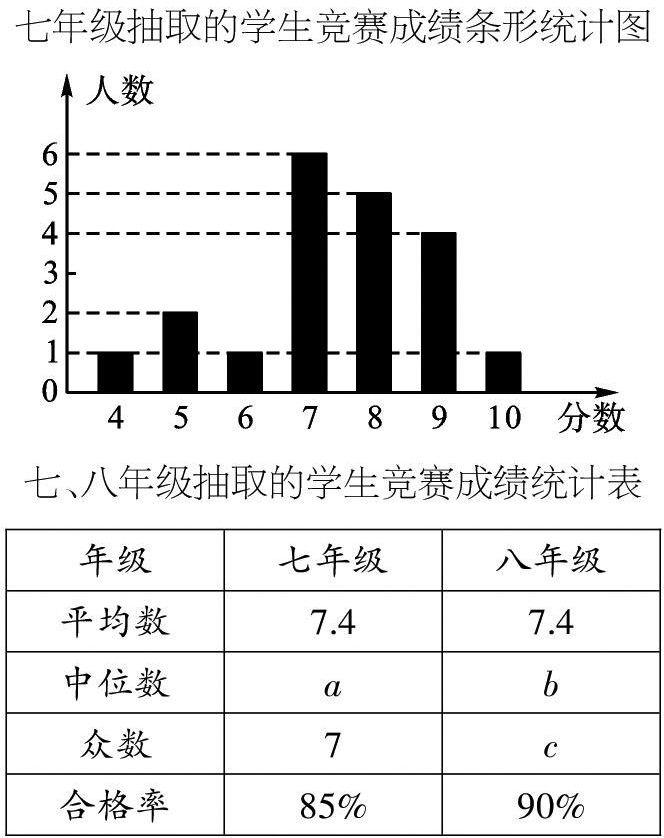
例2 （2020·重庆B卷）每年的4月15日是我国全民国家安全教育日。某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）。相关数据统计、整理如下：

八年级抽取的学生的竞赛成绩：

4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10。

根据以上信息，解答下列问题：

（1）填空：a=__，b=___，c=___;

（2）估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数;

（3）根据以上数据分析，从一个方面评价两个年级学生“国家安全法”知识竞赛的成绩谁更优异。

【分析】本题考查数据的代表值和用样本估计总体。

（1）从图表中获取数据信息，根据中位数和众数的意义确定a、b、c;

（2）利用样本估计总体思想：用樣本成绩达到9分及以上的人数所占的百分比来估计总体成绩达到9分及以上的人数所占的百分比即可;

（3）通过比较两个年级样本的中位数、众数或9分及以上人数所占百分比的大小，可以判断谁的成绩更优异。

解：（1）由图表可得。a=7+8/2=7.5，b=8+8/2=8，c=8。

（2）设七年级有学生x人，则八年级有（800-x）人，由题意，得

或整体思想考虑：

该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数=800×5+5/40=200（人）。

答：估计该校七、八年级800名学生中竞赛成绩达到9分及以上的人数为200人。

（3）答案一：八年级的成绩更优秀。理由：八年级被抽取学生成绩的中位数是8，而七年级被抽取学生成绩的中位数是7.5，从这一统计量看，八年级成绩更优秀。

答案二：八年级的成绩更优秀。理由：八年级被抽取学生成绩的众数是8，而七年级被抽取学生成绩的众数是7，从这一统计量看，八年级成绩更优秀。

答案三：八年级的成绩更优秀。理由：八年级被抽取学生成绩的合格率是90%，而七年级被抽取学生成绩的合格率是85%，从这一统计量看，八年级成绩更优秀。

【点评】本题考查中位数、众数、平均数的意义和计算方法，理解各个概念的内涵和计算方法是解题的关键。