利用粗糙集和双隐层BP 神经网络的小麦籽粒品种分类

吴尚智，周 运，王欢欢，徐丹丹

（西北师范大学 计算机科学与工程学院，兰州 730070）

小麦是一种在世界各地广泛种植的三大谷类作物之一，我国是世界上小麦消费大国，优质小麦的需求量越来越大[1-2]。为了实现小麦丰量不减产的目标，选育具有更好抗病虫害性且能适应各地环境，高产品质双重保障的小麦种子迫在眉睫。 研究者从试验田中选取样本进行品种改良，可能因动物传播者污染试验样本源等不可抗力因素影响，提取到错误待培育品种，与原试验对象无法做改进后对比。目前主要防治措施有物理防控和化学防治，但此类方法耗时耗力，急需一种快速且简便的小麦品种分类途径[3]。 针对在小麦品种识别、分类的应用问题，已有图像处理、模式识别、神经网络等学科方面开展研究。 孟惜等[4]以6 个小麦品种为对象，对籽粒图像进行中值滤波阈值预处理，特征提取并且结合PCA 降维，避免BP 网络陷入多点局部极小，用PSO 算法优化网络权值。 VHRMHULHN 等[5]对抽取的77 份DW 和 180CW 小麦样品做区分，形态学方法与近红外（NIR）光谱方法相结合，偏最小二乘法判别分析，准确率达99%。 CHARYTANOWICZ 等[6]利用x射线图像进行小麦籽粒分类的几何特征评价，主成分分析和多元因子分析相结合的方法，使用多变量统计方法，前3 个因子解释的籽粒变异率达到89．97%。 上述研究表明，针对小麦籽粒识别和分类的研究已经有所成果，但由于实际生产中所获取信息的不确定、强干扰性，需要确保多维度样本试验结果的高准确率，良好的识别效果。

本研究将粗糙集和双隐层BP 神经网络结合的方法应用于小麦种子品种识别中， 协助试验者完成品种培育、改良，更好地投入各地方生产，达到更加有效地抗病虫害、高产丰收目的。

1 理论基础

1.1 粗糙集

粗糙集（rough set，RS）作为数值分析理论由波兰数学家PAWLAK 于1982 年提出，用于处理模糊和不确定性知识的数学工具[7]。

定义1：知识与知识库。 所研究的对象所组成的非空有限集合为论域U，对∀X⊆U，称为U 中一个概念（包括空集Ф），论域中任何概念族通常简称知识。 对于一个完整的知识表达系统，即为一个知识库。

在粗糙集理论中，将信息表知识表达系统定义为S=＜U,R,V,f＞，其中U 为论域；R=C∪D 为属性集合（C数，通过函数f 可以确定U 中每一个对象Xi的属性值。

定义2：属性的上近似和下近似。 根据X 关于属性集合R 的上、下近似值概念，定义式（1）和式（2）：

定义3：知识的核。 知识库K(U,R)，属性集合R=C∪D，核描述为所有约简的交集，若有一等价关系族P∈R，满足core(P)=∩red(P)，则记为等价关系族集P 的核。简单来说，核即为等价关系族中所有重要属性的集合。

定义 4：约简。 定义决策表 S=(U,C∪D)，其中属性 C∩D=Ф。 令 Ф⊂X⊆C，Ф⊂Y⊆D，U/Y≠U/δ={U}(δ 是全体划分)。 若有X0⊆X 满足：(1)SX0(Y)=SX(Y)，即决策属性Ф⊂Y⊆D 关于条件属性Ф⊂X⊆C 的支持子集相等于决策属性 Y⊆D 关于条件属性 X0⊆X 的支持子集。 (2)SX(Y)⊃SX'(Y)，若 X'⊂X0⊆X。

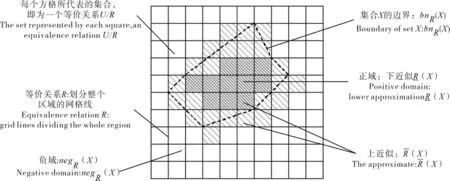
图1 粗糙近似图Figure 1 Rough approximation diagram

按照上述描述，总能找到X 的一个极小子集X0，即称X0是X 的一个约简。 空集Ф 的约简为Ф。

在粗糙集理论中，用上下近似集对不精确范畴近似定义，通过对模糊、不确定知识以集合定义、逼近方式达到知识判断的目的。 信息熵是系统不确定信息的量化指标[8]。 通俗说，熵越大，事件发生概率越低，表明信息所携带的不确定性越大；熵越小，结论与前述相反。

设有随机试验，X1，X2，…，Xn是论域 U 的一个划分，实验结果中每个 Xi有概率 pi=P(Xi)出现，简记 X=(p1，p2，…，pn)。 信息源 X 的信息熵定义公式为：

条件熵：知识Q 相对于知识P 的条件熵定义公式为：

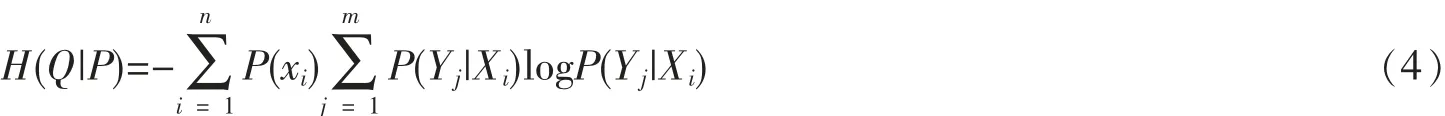
1.2 双隐层BP 神经网络

通常单计算层感知器可以通过增加隐层节点数，构建任意形状凸域，输出层节点对域内域外样本分类。通过增加第二个隐层，判断域形状能够任意组合，多层感知器能够处理任何复杂模型下的线性不可分问题。正因其表现优越的多维函数映射能力、鲁棒性、自学习能力，BP 神经网络如今仍被广泛使用[9-11]。

1.2.1 数据预处理 感知器输入输出数据预处理操作， 对具有不同量纲的BP 神经网络数据规划变化范围至[0，1]或[-1，1]，避免密集数据区分量取值太过集中，可有效使样本分布均匀，拉开距离。

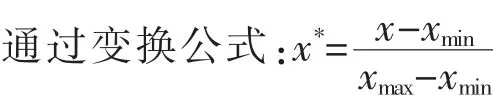
式中：xmin、xmax为矩阵 x 的最小值、 最大值；x 为矩阵原属性值；x*为归一化后BP 网络输入样本。

1.2.2 模型设计 BP 神经网络的学习由信号的正向传播和误差的反向传播两个过程组成。 使用反向传播算法逐步优化，依据最小化损失函数不断调整，得到每个感知器的权向量[12]。 其给出结构为N1-N2-N3-3 的双隐层网络图2。

2 粗糙集和BP 神经网络结合

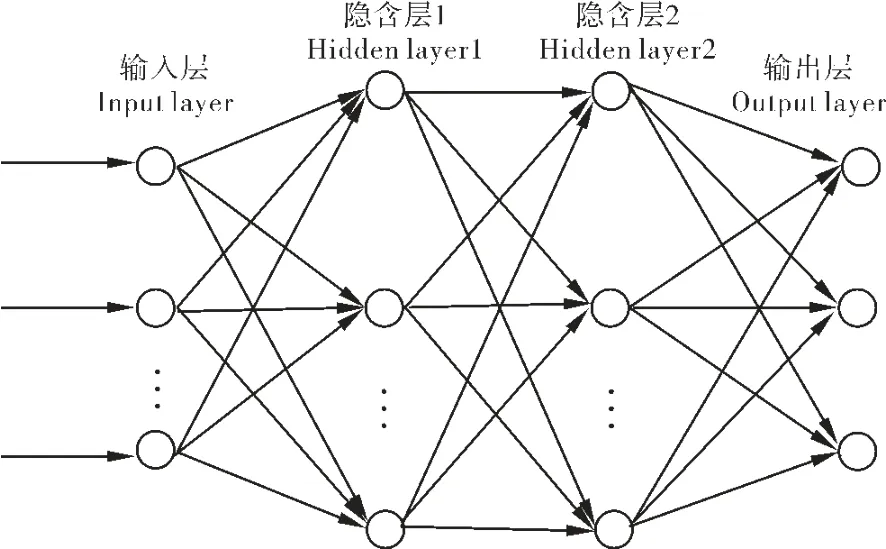
图2 双隐层BP 网络结构图Figure 2 BP network structure diagram of double hidden layer

本研究结合粗糙集和双隐层BP 神经网络建立小麦籽粒品种分类的模型。 由神经元作为信息处理单元，能对多个输入样本的模式向量组成的空间完成非线性映射，且具有较强的容错性、自适应性、泛化能力，但面对大维度空间数据处理效率较低。 粗糙集无法描绘属性值间的非线性关系，但在处理多维度空间信息时，能对冗余、无价值信息判断，简化得到有用信息。 两者优势互补，能有效提升神经网络整体性能。

2.1 方案设计

首先选取试验数据样本，构建原始决策表。设置聚类数目、迭代次数，用K-Means 方法聚类离散化，待质心不显著移动，表明聚类已经收敛，获得离散化后的决策表。其次用基于条件信息熵的启发式知识约简算法约简已经离散化后的决策表，剔除冗余属性，避免因训练样本数目过多而耗时过长。最后将约简的最小属性集充作BP 神经网络输入层指标， 决策属性D 作为输出指标，BP 作为对非线性可微分函数权系数优化的多层前馈网络，需在设置参数和确定网络结构后，确定双隐层BP 网络模型。 建模流程图如图3。

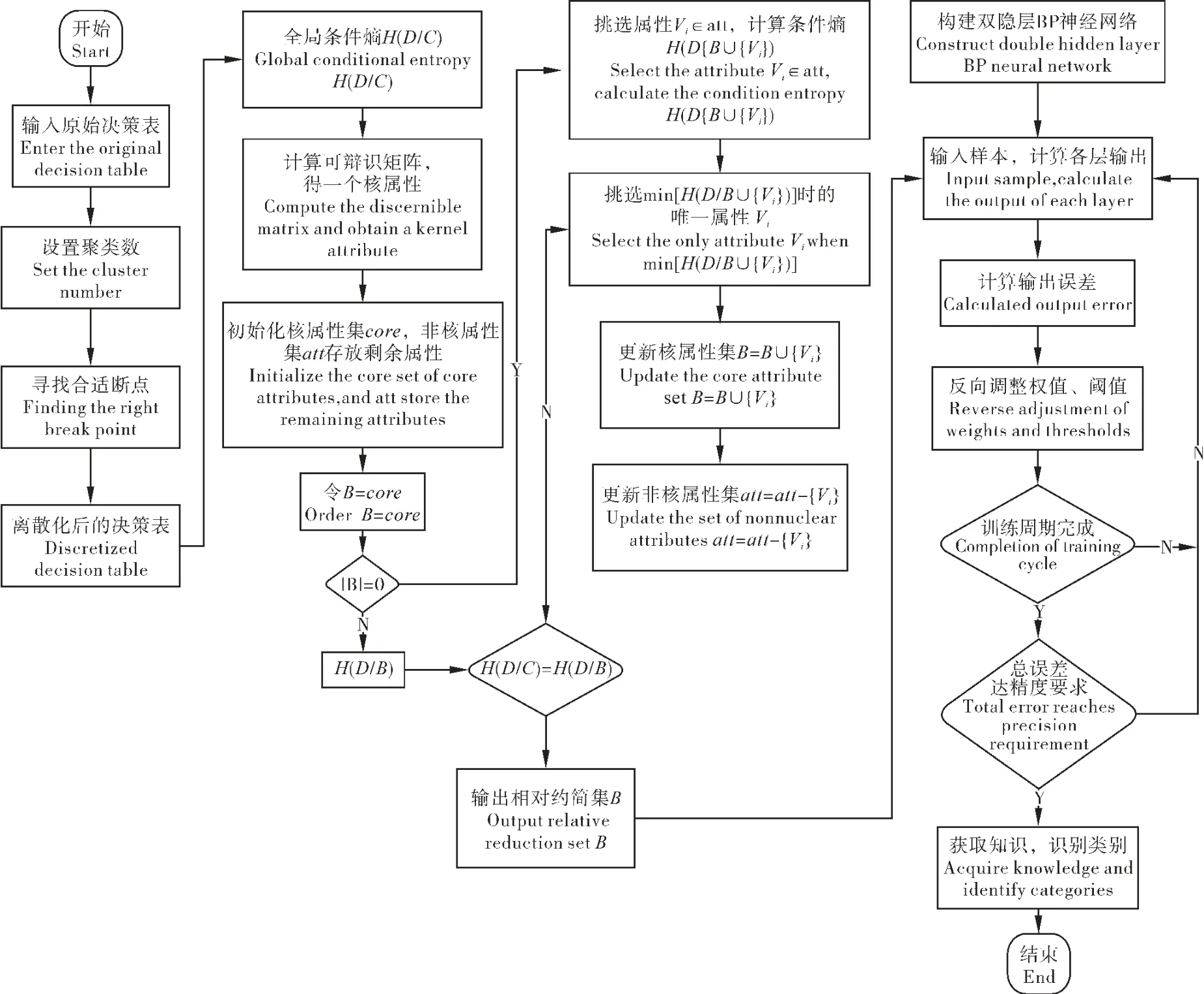
图3 RS+BP 神经网络建模流程图Figure 3 RS+BP neural network modeling flow chart

2.2 步骤描述

基于条件信息熵的约简算法将条件熵作为启发知识，针对不一致信息决策表，以决策表核为出发点，从非核属性集att 中依次挑选剩余属性集合，条件熵较小属性移入核属性集core，并随之将先前挑选出的属性从非核属性集att 中剔除。特殊情况下，可能发生多个属性含有相同决策的参考重要度，此时，则选择与约简结果集B 组合数最小的属性[13-14]。 若核属性集合存在，属性约简后的结果集条件熵H(D|B)=H(D|C)，集合B便存放着试验结果集。

算法时间复杂度主要是通过可辨识矩阵计算决策表核，以及从非核属性集att 中依次计算决策属性D 相对每个条件属性core∪{Vi}的条件熵。 步骤1～5 为属性约简描述。

Step1：求解全局条件熵H(D|C)，用于终止条件的判断。 同时，对离散化后的决策表S，分别设置核属性集core和非核属性集att 为空集。

Step2：计算可辨识矩阵[15]，挑选决策属性不等时条件属性组合数目为1 的属性作为核。 算法以此为起点，令约简结果集B=core。

Step3：从非核属性集att 中挑选每个属性Vi∈att，计算条件熵H(D|B∪{Vi}) 。

Step4：寻找出条件熵最小的那个属性（熵越小，表示含有的信息不确定性越小）。 每挑选出一个核属性Vi，即将该属性从非核属性集att 中减去。

Step5：挑选完整个条件属性集合后，记录核属性集合B。终止条件是判断初始条件属性集合的条件熵相等于约简后属性集合的条件熵，若H(D|C)=H(D|B)任务完成，否则转Step2。

原始决策表中样本经离散化预处理后，再由基于条件熵的属性约简算法降维，去除掉知识表达系统冗余、相互干扰的样本，使得双隐层BP 网络具有更佳逼近能力，泛化能力更强。 经上述步骤处理后，约简后最小属性集作为BP 网络输入层样本训练。 步骤6～步骤10 为BP 算法描述。

Step6：初始化权值矩阵 W1i1，W2j2，W3k3，并设置阈值 θi1，θj2，θk3，网络精度 ε，学习率 η。

Step7：将约简整理后的决策表作为BP 网络的训练样本。 前一层输入向量与连接权重的乘积，经激励函数转换后作为下一层的输入值，即前一层的输出作为下一层的输入。

Step8：计算每层输出值、网络输出误差。 每层神经网络的输出进行变换处理，变换函数f(x)采用单极性Sig鄄moid 函数，即：

隐含层1：隐层 1 上第i 个节点的总输入、输出分别为si1、zi1，隐层 1 总输出y1。

隐含层2：隐层 2 上第j 个节点的总输入、输出分别为si2、zj2，隐层 1 总输出y2。

输出层：输出层的第K 个节点的输出ok。

均方误差定义

Step9：获得神经元的误差信号后，利用误差反向调整每层权值、阈值，直至网络性能达到预设精度。 权值调整公式为：

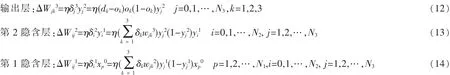
备注：δi为隐含层误差项，xij为结点 i 到结点 j 的输入，wij表示对应的权值，系数 η∈(0，1)为学习率。隐含层 1，2 总输出记为 y1，y2。

Step10：判断网络的总输出误差是否达到预期精度要求。 若E总≤ε，则算法结束；否则转至7 步，开始BP 算法新一轮。

3 实例结果与分析

3.1 数据预处理

小麦种子数据集（Wheat Seeds DataSet）来源于UCI 数据库。 用软X 射线技术和和颗粒包给定种子的计量数据，涉及对不同品种的小麦种子几何特征测定，用于分类、聚类任务。数据表1 中，一共210 个观察值，7个输入变量和 1 个输出变量。 变量名解释，V1：区域；V2：周长；V3：压实度；V4：籽粒长度；V5：籽粒宽度；V6：不对称系数；V7：籽粒腹沟长度，构成决策表条件属性集合 C。 决策属性 D 分为（1，2，3）3 类。

对表1 决策表应用IBM SPSS Statistics 20．0 统计软件对条件属性值离散化。 试验需将小麦样本品种分为3 类，故选用K-means 聚类数目3，设置迭代次数为10，当且仅当聚类中心更改为．000，说明聚类已经达到收敛，中心的最大绝对坐标不再发生改变。 初始、最终聚类中心变化如表2。

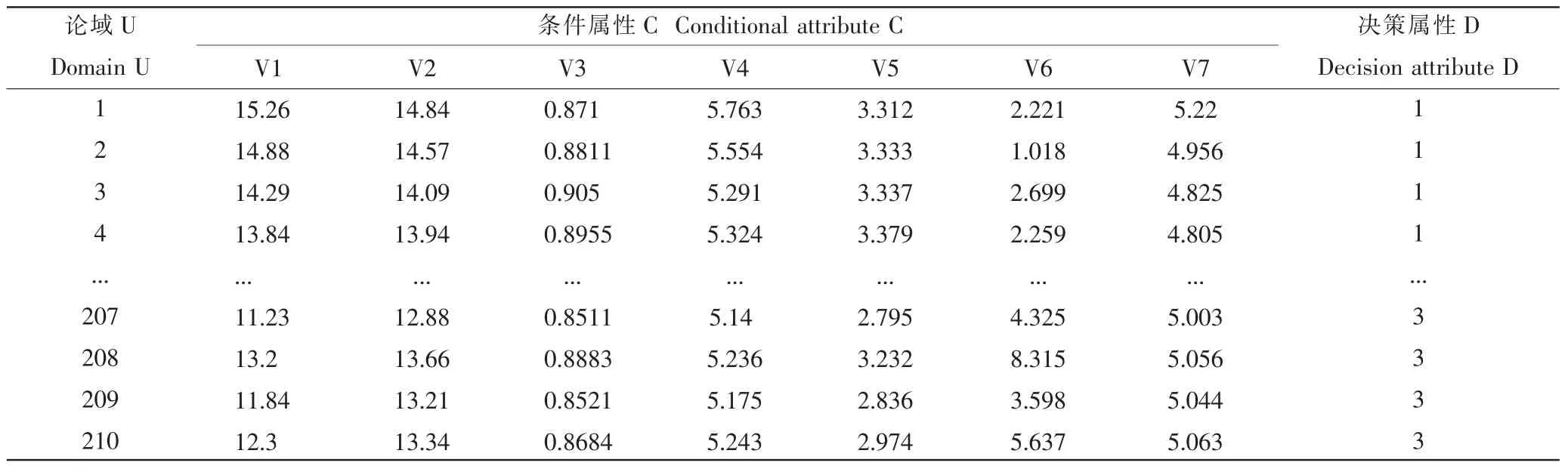
表1 原始信息决策表Table 1 Original information decision table

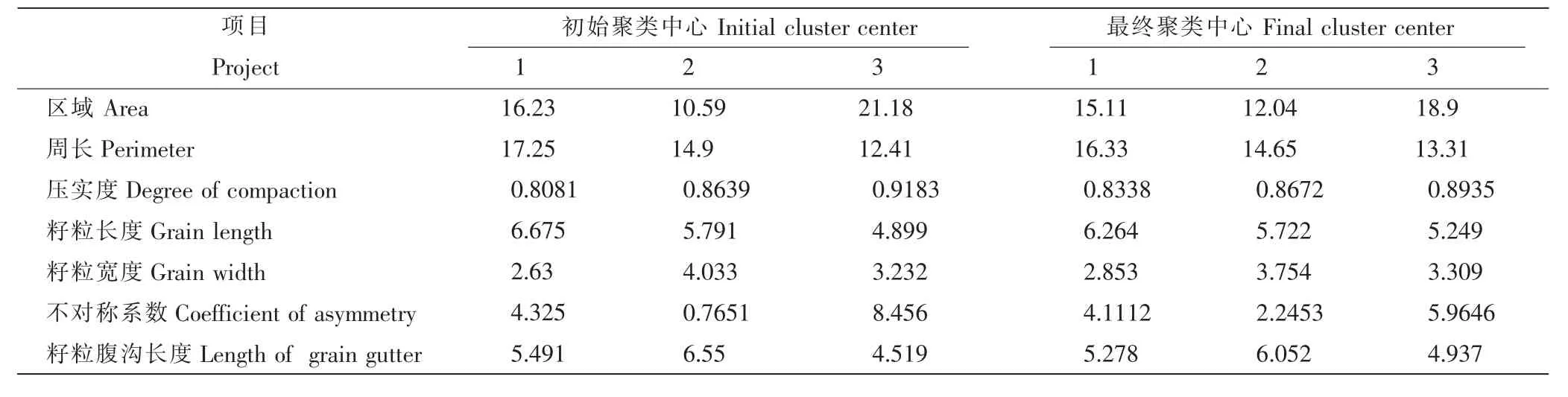
表2 初始、最终聚类中心Table 2 Initial and final clustering center

选用基于划分的K-means 聚类算法，以欧氏距离计算簇内对象间相似度，将两两相似度大的对象归于同一类簇，并用1，2，3 数字标记实际连续数值，实现连续属性离散化[16]。 基于条件信息熵的属性约简对小麦种子样本预处理，并且在不影响整体分类能力的情况下，剔除冗余属性，加快网络收敛速度。 离散化并约简后的决策如表3。

决策表中离散化后的数据若作为双隐层神经网络训练样本输入，需要通过单极性Sigmoid 变化函数归一化处理，避免因为连续型数值过大导致神经元输出饱和，且造成随着训练次数增加，在最佳训练时刻之后，训练误差持续下降而测试误差呈现相反现象。

信号的正向传播学习过程中，输出信号会与教师信号做差值比对，依照误差值反向计算输出层、双隐含层误差信号并调整权值。 若不做调整，可能产生的结果为：（1）具有不同量纲的网络输入分量因变化范围不一致，造成感知器每个节点无法很好地接收外来信息。 （2）对于实际信号的输出会偏离教师信号，一轮网络训练结束后，可能结果是总输出误差H 中所属比例大的输出分量相对误差小。

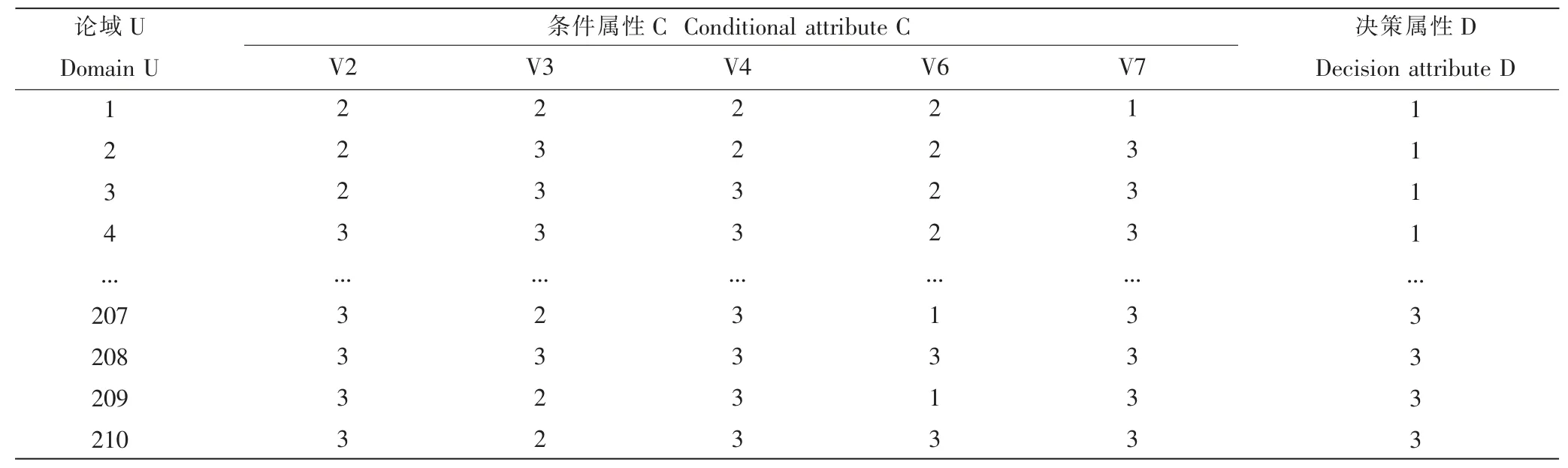
表3 离散化后的决策表Table 3 Discretized decision table

3.2 试验结果及分析

由于单隐含层网络非线性映射能力较弱，对于线性不可分数据，通过添加含有多个线性二分类器的隐含层，使得难以可视化的高维数据变得线性可分[17]。 设计双隐层BP 网络，主要考虑到当单层感知器无法改善网络性能且不具有降低网络训练误差的能力，双隐层结构在处理不连续函数逼近问题时，呈现出拟合能力强、训练误差小、辨识精度高等优点，但不是所有双隐层结构网络都有优越性能，与此同时不足在于：多层感知器结构的设计更加复杂，样本训练时间加长。 因此，应依据具体网络模型进行结构设计。

由于双隐层神经元个数的选择具有主观性，通过“试凑法”，为表现不同节点下同一样本的网络性能，本研究中通过训练结果的MSH（均方差）多次调整寻找隐含层个数，最终确定网络结构为：5-10-3-3。 部分测试结果如表4。

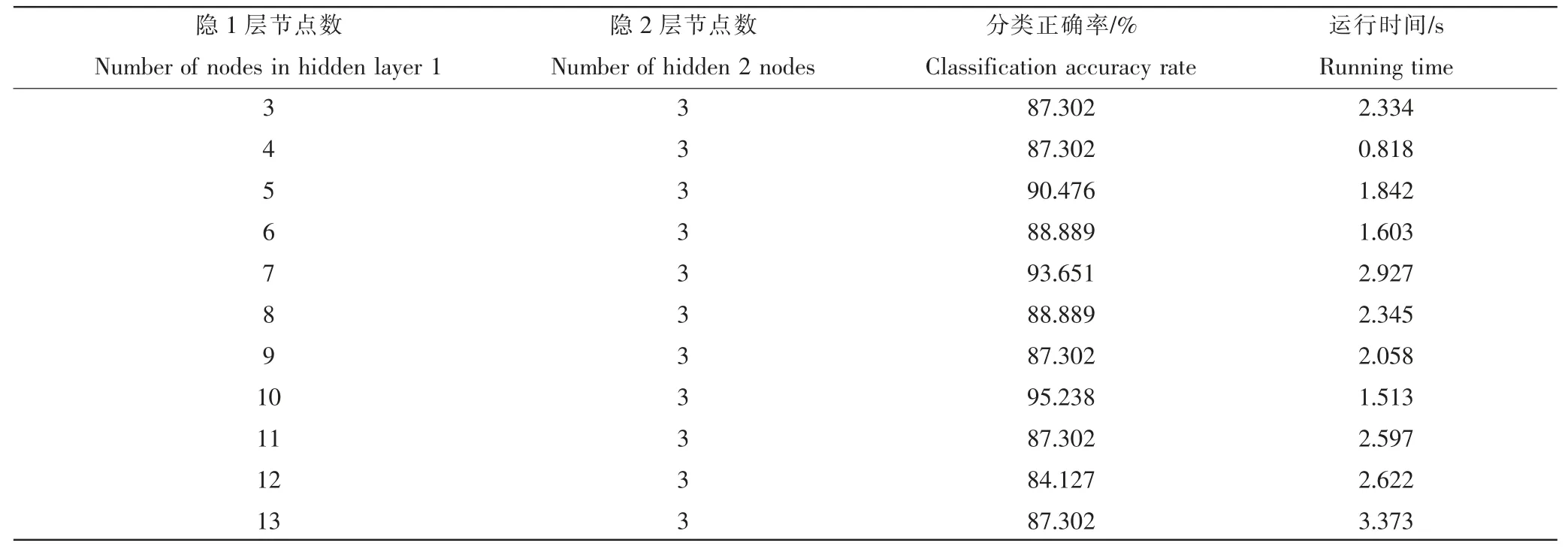
表4 部分不同双隐含层神经元个数时的网络性能Table 4 Network performance of some neurons with different double hidden layers

在科学和工程问题中， 希望通过直线或者多项式方程拟合平面上大量散落的数据点，MATLAB 中可以用函数plotfit、curvefit 进行曲线拟合。 网络训练预测时，MATLAB 自动将数据分为训练、验证、测试，回归系数R 越接近1，表示试验效果越好。 但与此同时，可能会出现过拟合现象，即出现学习过程过于精确，对训练数据外的数据泛化能力降低。 原因通常有很多，如训练数据量不够，无法对待测试数据拟合；或者样本含有噪声，对网络性能有影响。 常见解决方法有：提前停止法、隐层节点自生成法、正则化等[18]。 此次试验并未出现过拟合现象，且表现性能良好。 具体拟合情况如图4。

在确定双隐层BP 网络参数选择和结构设计后，需要抽取样本数据通过多个周期测试除训练集合外的待预测样本，倘若网络模型下的数据拟合能力较差劲，对非规律样本内容预测能力同样很差，此时即为训练过度[19]。 若因样本数过少或网络模型复杂性过低造成的欠拟合现象，可通过减少正则化参数、换用非线性模型等方法避免。

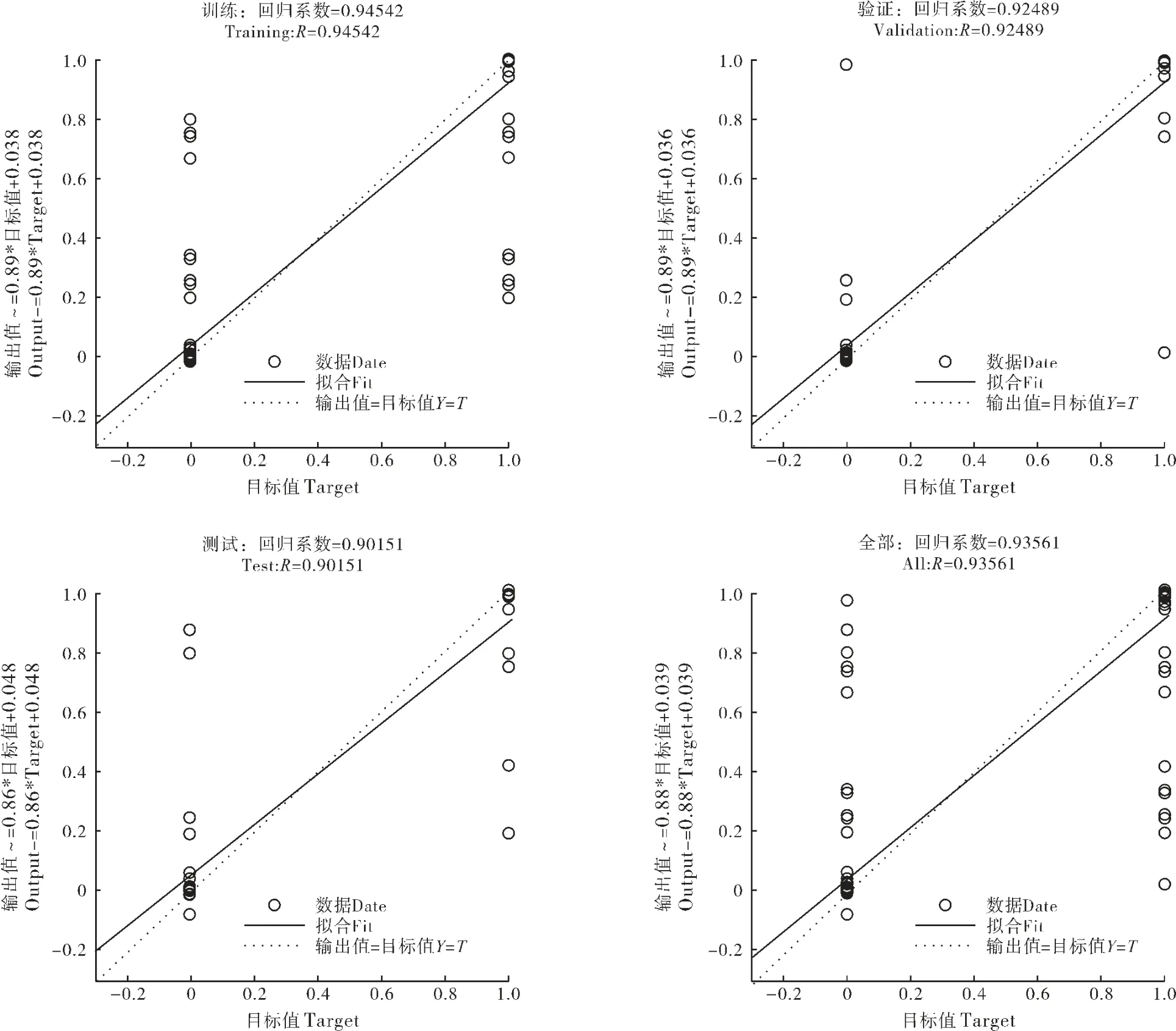
图4 回归分析图Figure 4 Regression analysis diagram

本研究中设定网络性能目标均方误差MSE 为0.005，试验在迭代19 次后终止，用时1.513s。 为验证所选模型的泛化能力， 将样本数据分割出交叉验证集合，用来检验所选BP 网络模型优劣与否。 图5 显示最佳验证性能0.041381， 小于设定值并在迭代次数为第13 次时停止训练。纵坐标最小均方误差表示实际输出值与真实数据输出的拟合程度，性能图中训练集开始时误差较小只有0.035，验证集误差0.063，两者相差大，低方差表示模型稳定选择合适； 测试集误差0.03 与训练集相差不大，为低偏差，说明模型拟合程度较高。

为证明RS+双隐层BP 神经网络相比于传统BP网络具有可行性， 在保证使用相同神经网络结构的前提下，对相同数据(样本的30%)进行测试，对比准确率并将效果图可视化， 可知约简后分类准确率有明显提高，约简前后分类对比图6 和图7。

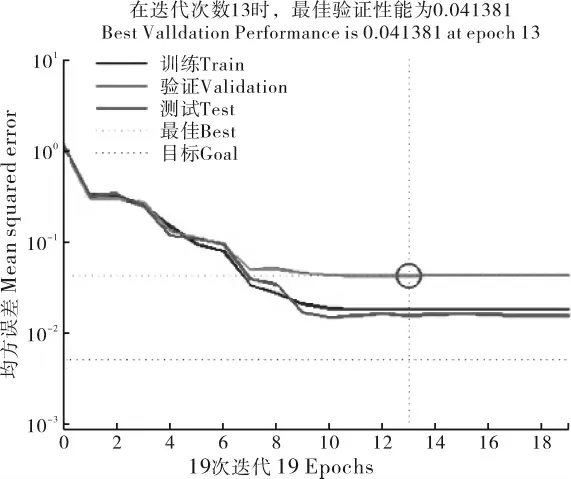
图5 性能图Figure 5 Performance diagram

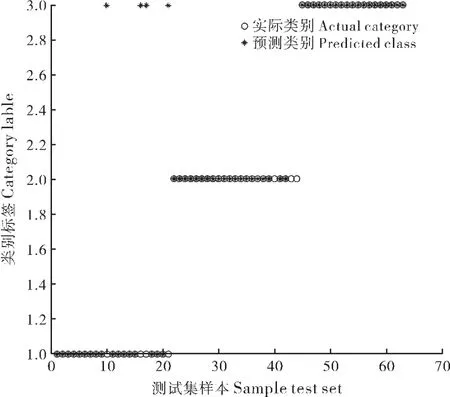
图6 传统神经网络测试样本分类效果Figure 6 Traditional neural network test sample classification renderings

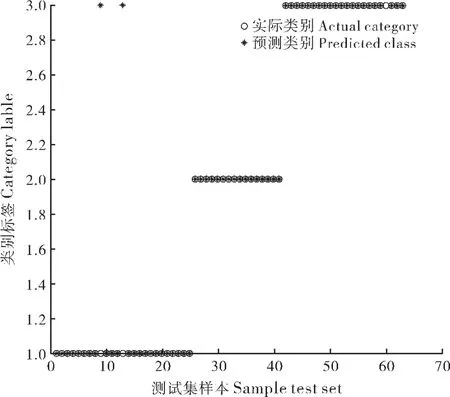
图7 RS+BP 神经网络测试样本分类效果图Figure 7 Classification effect diagram of RS+BP neural network test samples

针对神经网络无法对冗余信息进行有效判断的缺陷，运用基于条件信息熵的属性约简算法，将初始决策表7 个条件属性约简至5 个，降低数据集维度，使其对大维度空间信息具有更好适应性。 表5 给出约简前后比较结果。

由表5 可知， 约简后的数据样本应用RS+双隐层BP 神经网络训练，与传统BP 网络训练原始数据比，7维特征属性约简至5 维，数据集维度降低，训练样本所需运行时间减少和分类准确率大幅度提高。

4 讨论与结论

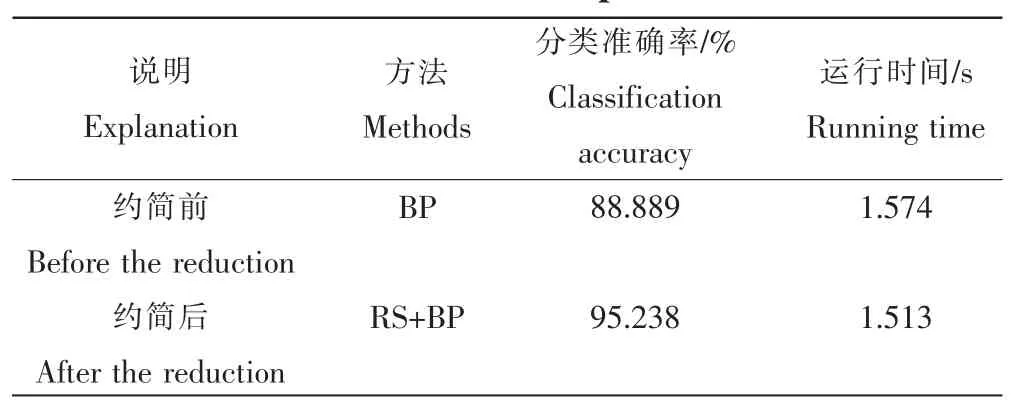
表5 约简样本前后效果对比Table 5 Comparison of effect before and after reduction samples

数据挖掘作为信息时代从大量数据中获取有价值信息进行数据分析的必要步骤，通过相关性分组、分类、聚类、描述和可视化等方法，应用于模式识别、数据分析等诸多领域。 BASATI 等[20]使用基于监督和非监督模式识别方法的Vis/NIR 光谱(波长范围350～1000nm)分析了健康和5%、10%、15%和20%不健康5 类样品，研究用PCA 建模的SIMCA 模式分类健康、不健康两类样品，准确率达100%。 陈文根等[21]利用深度卷积神经网络提取小麦特征参数，用Softmax 分类器识别，针对大样本下的学习过程，具有很强的泛化性，该方法平均识别准确率达97．78%。 樊超等[22]对采集到的小麦颗粒图像进行中值滤波后，采用迭代式阈值法分割图像，提取出特征，然后通过构建神经网络研究了小麦品种的识别准确率与品种数量之间的关系。本试验研究发现，预处理条件属性，剔除对分类准确率有干扰的冗余数据，经BP 神经网络训练后，可以明显降低运行时间且提高分类准确率，有效选育出优质的小麦籽粒品种。 若神经网络因输入量大，使得网络泛化能力差、分类精度低、收敛速度大幅度降低，就需要降低神经网络的输入维度，简化神经网络结构。

粗糙集与神经网络结合，在小麦籽粒品种分类的试验过程中，针对传统人工神经网络处理多维冗余信息表现出的拟合误差大，分类精度较低缺陷。 首先K-means 聚类预处理数据，粗糙集约简算法简化数据集、降低维度，同时改变神经网络拓扑结构，使用双隐层BP 网络提升训练精度、缩短训练时间。 试验表明，该方法使得分类准确率由88．889%提升至 95．238%，运行时间 1．574s 缩短至1．513s，具有更佳的准确率保证，避免人力识别的资源浪费，训练过程中快速地做出品种判断，在农业生产中小麦种子品种分类应用中具有很好的实用价值。